数据结构与算法（五）回溯算法（Java）

一、简介

1.1 定义

回溯法（back tracking）是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回到上一步重新选择，这种走不通就退回再走的技术为 回溯法，而满足回溯条件时某个状态的点称为 “回溯点”。

1.2 特性

回溯法是一个既带有 系统性 又带有 跳跃性 的搜索算法。

系统性： 它在包含问题的所有解的解空间树中，按照 深度优先的策略，从根节点出发搜索解空间树。
跳跃性： 算法搜索至解空间树的任一结点时，判断该结点为根的子树是否包含问题的解，如果肯定不包含，则跳过以该结点为根的子树的搜索，逐层向其始祖结点回溯。否则，进入该子树，继续深度优先的策略进行搜索。

这种以深度优先的方式系统地搜索问题解的算法称为回溯法，它 适用于解一些组合数较大的问题。

1.3 结点知识补充

扩展结点： 一个 正在生成儿子 的结点，称为扩展结点。
活结点： 一个 自身已生成但其儿子还没有全部生成 的结点，称为活结点。
死结点： 一个 所有儿子已经全部生成 的结点，称为死结点。

深度优先策略：

如果对一个扩展结点 R，一旦生成了它的一个儿子 C，就把 C 当作新的扩展结点。
在完成对子树 C（以 C 为根的子树）的穷尽搜索之后，将 R 重新变成扩展结点，继续生成 R 的下一个儿子（如果存在）。

广度优先策略：

在一个扩展结点变成死结点之前，它一直是扩展结点。

回溯法：

为了避免生成那些不可能产生最佳解的问题状态，要不断地利用 限界函数（bounding function）来处死那些实际上不可能产生所需解的活结点，以减少问题的计算量。
具有剪枝函数的深度优先生成法称为回溯法。

那什么是限界函数呢？限界函数是剪枝函数的一种，下面我们一起来看下剪枝函数。

1.4 剪枝函数

剪枝函数：当某个顶点没有希望，则其所在的树枝可以减去。

剪枝函数一般有两种：

约束函数： 剪去不满足约束条件的路径。
限界函数： 减去不能得到最优解的路径。

1.5 使用场景

回溯就是递归的副产品，只要有递归就会有回溯。 其实回溯就是 递归搜索+剪枝，并不是什么高效的算法。

回溯算法的应用：

当问题是要满足某种性质（约束条件）的所有接或最优解时，往往使用回溯法。

1.6 解空间

当确定回溯后，问题的关键转化为如何定义问题的解空间，且转化为树结构，可以称之为 解空间树。

解空间树分为：

子集树： 当所给的问题是 从 n 个元素的集合中找到某种性质的子集 时，相应的解空间变为子集树。如：0-1 背包问题，从所给重量、价值不同的物品中挑选几个物品放入背包，使得在满足背包不超重的情况下，背包内物品价值最大。
排列数： 所给的问题是确定 n 个元素满足某种性质的排列时，相应的解空间就是排列树。如：旅行问题，一个人把几个城市旅游一遍，要求走的路程最小，它的解法就是几个城市的排列。

1.7 实现模板

// 一定要分成横纵两个方面思考问题
public void backTracking(参数) {if (终止条件) {// 存放结果return;}// 注意 i=0,i=start 的区别for (选择：本层集合中元素（树中结点孩子的数量就是集合的大小）) {// 处理节点backTracking(路径，选择列表); // 递归，注意 i 和 i++ 的区别// 回溯，撤销处理结果}
}

二、经典示例

2.1 0-1 背包问题

题目：

有一个背包，容量由你自己输入，有n个物品，每个物品都具有容量与价值，这些都是由你自己输入的，请问，要怎么放物品到背包里，才能使得总价值最大呢，放入背包的总容量要小于等于背包的总容量。（如果一个物品放不下，则可以拆分成多个小块）
背包：M：100
物品：N：7
重量价值
10 20
20 40
30 30
25 20
50 40
10 35
60 70

思路：

迭代进行深度优先遍历；
如果重量超出容量不予考虑；
不超出容量情况下，获取价值最大值。

代码实现：

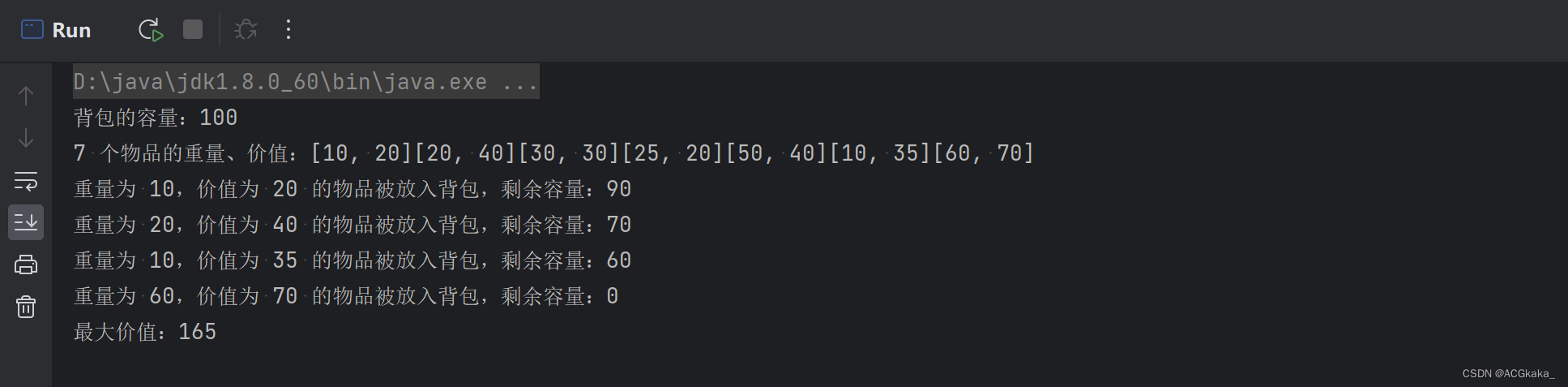
public static void main(String[] args) {int[][] items = new int[7][2];// 重量 价值items[0][0] = 10; items[0][1] = 20;items[1][0] = 20; items[1][1] = 40;items[2][0] = 30; items[2][1] = 30;items[3][0] = 25; items[3][1] = 20;items[4][0] = 50; items[4][1] = 40;items[5][0] = 10; items[5][1] = 35;items[6][0] = 60; items[6][1] = 70;int capacity = 100;System.out.println("背包的容量：" + capacity);StringBuilder builder = new StringBuilder();for (int[] item : items) {builder.append(Arrays.toString(item));}System.out.println(items.length + " 个物品的重量、价值：" + builder.toString());int maxValue = maxValue(items, capacity);System.out.println("最大价值：" + maxValue);
}private static int maxValue(int[][] items, int capacity) {// 0-未放入背包 1-放入背包int[] flag = new int[items.length];List<int[]> record = new ArrayList<>();int maxValue = maxValue(items, capacity, flag, 0, 0, record);for (int[] item : record) {capacity = capacity - item[0];System.out.println("重量为 " + item[0] + "，价值为 " + item[1] + " 的物品被放入背包，剩余容量：" + capacity);}return maxValue;
}private static int maxValue(int[][] items, int capacity, int[] flag, int weightSum, int oldMaxValue, List<int[]> record) {if (weightSum > capacity) {return -1;}int maxValue = oldMaxValue;for (int i = 0; i < items.length; i++) {if (flag[i] == 0) {flag[i] = 1;int tmpValue = maxValue(items, capacity, flag, weightSum + items[i][0], oldMaxValue + items[i][1], record);if (tmpValue != -1) {if (tmpValue > maxValue) {maxValue = tmpValue;record.clear();// 用于记录日志for (int j = 0; j < flag.length; j++) {if (flag[j] == 1) {record.add(items[j]);}}}}flag[i] = 0;}}return maxValue;
}

执行结果：

在这里插入图片描述

2.2 N皇后问题

N皇后

题目：

设计一种算法，打印 N 皇后在 N × N 棋盘上的各种摆法，其中每个皇后都不同行、不同列，也不在对角线上。这里的“对角线”指的是所有的对角线，不只是平分整个棋盘的那两条对角线。

注意：本题相对原题做了扩展

示例:

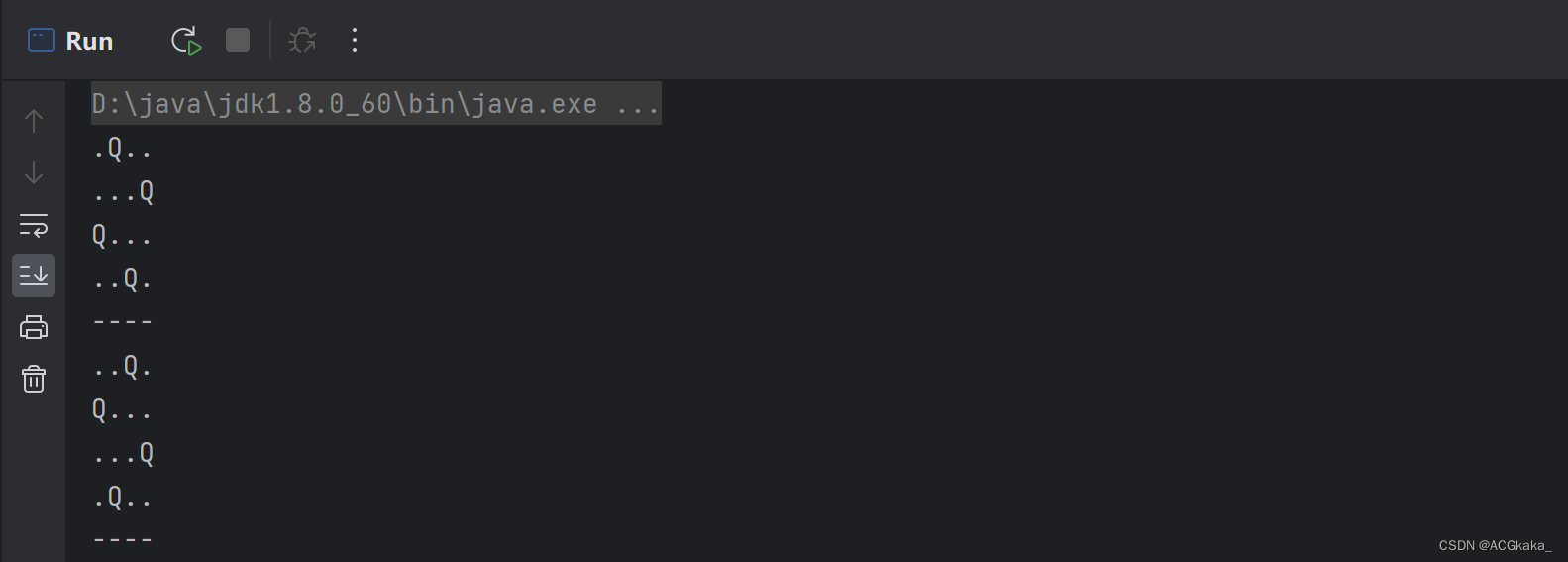
 输入：4输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]解释: 4 皇后问题存在如下两个不同的解法。
[[".Q..",  // 解法 1"...Q","Q...","..Q."],["..Q.",  // 解法 2"Q...","...Q",".Q.."]
]

代码实现：

public static void main(String[] args) {List<List<String>> result = solveNQueens(4);result.forEach(o -> {o.forEach(System.out::println);System.out.println("----");});
}public static List<List<String>> solveNQueens(int n) {List<List<String>> list = new ArrayList<>();handleQueens(n, 0, new int[n], new ArrayList<>(), new HashSet<>(), new HashSet<>(), list);return list;
}private static void handleQueens(int n, int level, int[] flag, List<String> queens, Set<Integer> diagonalSet, Set<Integer> reverseDiagonalSet, List<List<String>> list) {if (level >= n) {list.add(new ArrayList<>(queens));return;}for (int i = 0; i < n; i++) {int diagonal = i - level;int reverseDiagonal = i + level;if (flag[i] == 0 && !diagonalSet.contains(diagonal) && !reverseDiagonalSet.contains(reverseDiagonal)) {flag[i] = 1;queens.add(getLineStr(i, n));diagonalSet.add(diagonal);reverseDiagonalSet.add(reverseDiagonal);handleQueens(n, level + 1, flag, queens, diagonalSet, reverseDiagonalSet, list);reverseDiagonalSet.remove(reverseDiagonal);diagonalSet.remove(diagonal);queens.remove(queens.size() - 1);flag[i] = 0;}}
}private static String getLineStr(int i, int n) {StringBuilder builder = new StringBuilder();for (int j = 0; j < n; j++) {builder.append(j == i ? "Q" : ".");}return builder.toString();
}