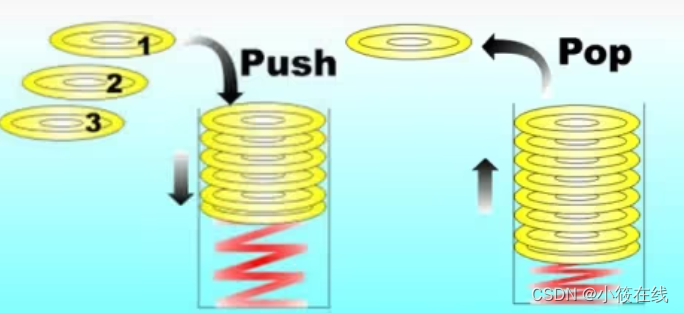
堆是一种基于完全二叉树的数据结构，它分为大根堆和小根堆。在大根堆中，每个节点的值都大于或等于其子节点的值；而在小根堆中，每个节点的值都小于或等于其子节点的值。

在Java中，我们可以使用数组来表示堆。由于完全二叉树的性质，我们可以将堆的节点按照从上到下、从左到右的顺序对应到数组中。假设堆的根节点在数组中的下标为0，则其左孩子的下标为2i+1，右孩子的下标为2i+2，父节点的下标为(i-1)/2。

以下是使用Java实现堆的代码：

public class Heap {private int[] heap;   // 堆private int size;     // 堆的大小public Heap(int[] heap) {this.heap = heap;this.size = heap.length;buildHeap();}// 堆排序public void sort() {while (size > 1) {swap(0, size - 1);size--;heapify(0);}}// 构建堆private void buildHeap() {for (int i = (size - 2) / 2; i >= 0; i--) {heapify(i);}}// 堆化private void heapify(int i) {int left = 2 * i + 1;int right = 2 * i + 2;int max = i;if (left < size && heap[left] > heap[max]) {max = left;}if (right < size && heap[right] > heap[max]) {max = right;}if (max != i) {swap(i, max);heapify(max);}}// 交换元素private void swap(int i, int j) {int temp = heap[i];heap[i] = heap[j];heap[j] = temp;}
}

上述代码实现了一个最大堆，堆的大小为数组的长度。堆排序的思路与普通的堆排序一致，先建立堆，然后每次将堆顶元素与堆底元素交换，缩小堆的大小，并重新堆化。

对于一个包含n个元素的数组，建立堆的时间复杂度为O(n)，堆排序的时间复杂度为O(nlogn)。由于堆排序的空间复杂度为O(1)，因此它是一种原地排序算法。