目录
写在前面
一、优化器介绍
1.SGD+Momentum
2.Adagrad
3.Adadelta
4.RMSprop
5.Adam
6.Adamax
7.AdaW
8.L-BFGS
二、优化器对比
优化器系列文章列表
Pytorch优化器全总结(一)SGD、ASGD、Rprop、Adagrad
Pytorch优化器全总结(二)Adadelta、RMSprop、Adam、Adamax、AdamW、NAdam、SparseAdam
Pytorch优化器全总结(三)牛顿法、BFGS、L-BFGS 含代码
写在前面
常用的优化器我已经用三篇文章介绍完了,现在我将对比一下这些优化器的收敛速度。
下面我将简单介绍一下要对比的优化器,每种我只用一到两句话介绍,详细介绍请跳转上面的链接,每种优化器都详细介绍过。
一、优化器介绍
1.SGD+Momentum
带动量 的SGD 优化算法,Momentum通过将当前梯度与过去梯度加权平均,来获取即将更新的梯度,有助于在相关方向上加速SGD并抑制振荡。
2.Adagrad
每个时间步长对每个参数使用不同的学习率。 引入了梯度的二阶矩,二阶矩是迄今为止所有梯度值的平方和,二阶矩的越大,代表步长的不确定性越大,学习率就越小,反之学习率越大。
3.Adadelta
对于每个维度,用梯度平方的指数加权平均代替了全部梯度的平方和,避免了后期更新时更新幅度逐渐趋近于0的问题。
用更新量的平方的指数加权平均来动态得代替了全局的标量的学习率,避免了对学习率的敏感。
4.RMSprop
与Adadelta同一时期,等价于实现了Adadelta的第一个改动。
5.Adam
同时使用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。 一阶矩来控制模型更新的方向,二阶矩控制步长(学习率)。
6.Adamax
在Adam的基础上,为学习率的上限限制了范围。将Adam的二范数(二阶矩估计)推广到无穷范数,因为无穷范数,就是取向量的最大值,这就为学习率的上限提供了一个更简单的范围。
7.AdaW
使用adam+权重衰减的方式解决了adam+L2正则化表现不佳的问题。
8.L-BFGS
牛顿法是基于迭代的二阶优化方法,对于高维的应用场景,求二阶导变得不可行;BFGS对牛顿法做了改进,用一阶导和一个基于迭代的矩阵H模拟海森矩阵,从而降低计算的复杂度;BFGS虽然对牛顿法做了优化,但是H的存储空间至少为N(N+1)/2(N为特征维数),需要的存储空间将是非常巨大的,L-BFGS采用加窗的方式,通过存储前m次迭代的少量数据来替代前一次的H矩阵,从而大大减少数据的存储空间。
二、优化器对比
下面我们将对比SGD、SGD+Momentum、Adagrad、Adadelta、RMSprop、Adam、Adamax、AdaW、L-BFGS的收敛速度。
代码如下:
import torch
import torch.utils.data as Data
import torch.nn.functional as F
from torch.autograd import Variable
import matplotlib.pyplot as plt# 超参数
LR = 0.01
BATCH_SIZE = 32
EPOCH = 12# 生成假数据
# torch.unsqueeze() 的作用是将一维变二维,torch只能处理二维的数据
x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1) # x data (tensor), shape(100, 1)
# 0.2 * torch.rand(x.size())增加噪点
y = x.pow(2) + 0.1 * torch.normal(torch.zeros(*x.size()))# 定义数据库
dataset = Data.TensorDataset(x, y)# 定义数据加载器
loader = Data.DataLoader(dataset=dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=0)# 定义pytorch网络
class Net(torch.nn.Module):def __init__(self, n_features, n_hidden, n_output):super(Net, self).__init__()self.hidden = torch.nn.Linear(n_features, n_hidden)self.predict = torch.nn.Linear(n_hidden, n_output)def forward(self, x):x = F.relu(self.hidden(x))y = self.predict(x)return y# 定义不同的优化器网络
net_SGD = Net(1, 10, 1)
net_Momentum = Net(1, 10, 1)
net_Adagrad = Net(1, 10, 1)
net_Adadelta = Net(1, 10, 1)
net_RMSprop = Net(1, 10, 1)
net_Adam = Net(1, 10, 1)
net_Adamax = Net(1, 10, 1)
net_AdamW = Net(1, 10, 1)
net_LBFGS = Net(1, 10, 1)# 选择不同的优化方法
opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR)
opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.9)
opt_Adagrad = torch.optim.Adagrad(net_Adagrad.parameters(), lr=LR)
opt_Adadelta = torch.optim.Adadelta(net_Adadelta.parameters(), lr=LR)
opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
opt_Adam = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
opt_Adamax = torch.optim.Adamax(net_Adamax.parameters(), lr=LR, betas=(0.9, 0.99))
opt_AdamW = torch.optim.AdamW(net_AdamW.parameters(), lr=LR, betas=(0.9, 0.99))
opt_LBFGS = torch.optim.LBFGS(net_LBFGS.parameters(), lr=LR, max_iter=10, max_eval=10)nets = [net_SGD, net_Momentum, net_Adagrad, net_Adadelta, net_RMSprop, net_Adam, net_Adamax, net_AdamW, net_LBFGS]
optimizers = [opt_SGD, opt_Momentum, opt_Adagrad, opt_Adadelta, opt_RMSprop, opt_Adam, opt_Adamax, opt_AdamW, opt_LBFGS]# 选择损失函数
loss_func = torch.nn.MSELoss()# 不同方法的loss
loss_SGD = []
loss_Momentum = []
loss_Adagrad = []
loss_Adadelta = []
loss_RMSprop = []
loss_Adam = []
loss_Adamax = []
loss_AdamW = []
loss_LBFGS = []# 保存所有loss
losses = [loss_SGD, loss_Momentum, loss_Adagrad, loss_Adadelta, loss_RMSprop, loss_Adam, loss_Adamax, loss_AdamW, loss_LBFGS]# 执行训练
for epoch in range(EPOCH):for step, (batch_x, batch_y) in enumerate(loader):var_x = Variable(batch_x)var_y = Variable(batch_y)for net, optimizer, loss_history in zip(nets, optimizers, losses):if isinstance(optimizer, torch.optim.LBFGS):def closure():y_pred = net(var_x)loss = loss_func(y_pred, var_y)optimizer.zero_grad()loss.backward()return lossloss = optimizer.step(closure)else:# 对x进行预测prediction = net(var_x)# 计算损失loss = loss_func(prediction, var_y)# 每次迭代清空上一次的梯度optimizer.zero_grad()# 反向传播loss.backward()# 更新梯度optimizer.step()# 保存loss记录loss_history.append(loss.data)# 画图
labels = ['SGD', 'Momentum', 'Adagrad', 'Adadelta', 'RMSprop', 'Adam', 'Adamax', 'AdamW', 'LBFGS']
for i, loss_history in enumerate(losses):plt.plot(loss_history, label=labels[i])
plt.legend(loc='best')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.ylim((0, 0.2))
plt.show()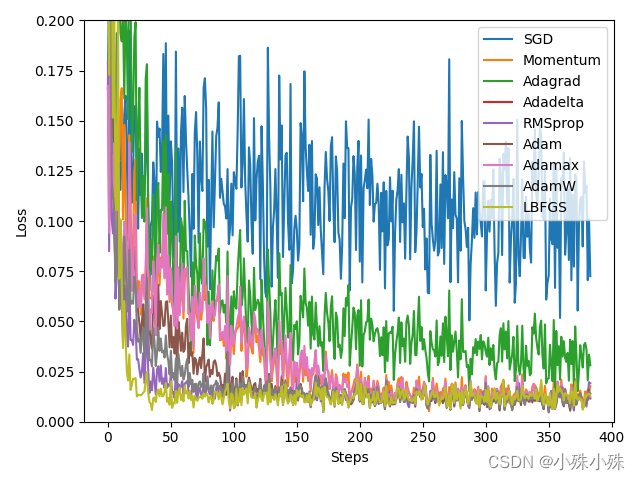
从图中可以看到,Adam、Adamax、AdaW、L-BFGS收敛速度要更快,当然这次实验只代表一般情况下的结果,项目中还是要以实际效果为准,大家在实际项目中还是要多试几种,选择适合自己的。
算法的性能比较就介绍到这里,收藏关注不迷路。
优化器系列文章列表
Pytorch优化器全总结(一)SGD、ASGD、Rprop、Adagrad
Pytorch优化器全总结(二)Adadelta、RMSprop、Adam、Adamax、AdamW、NAdam、SparseAdam
Pytorch优化器全总结(三)牛顿法、BFGS、L-BFGS 含代码