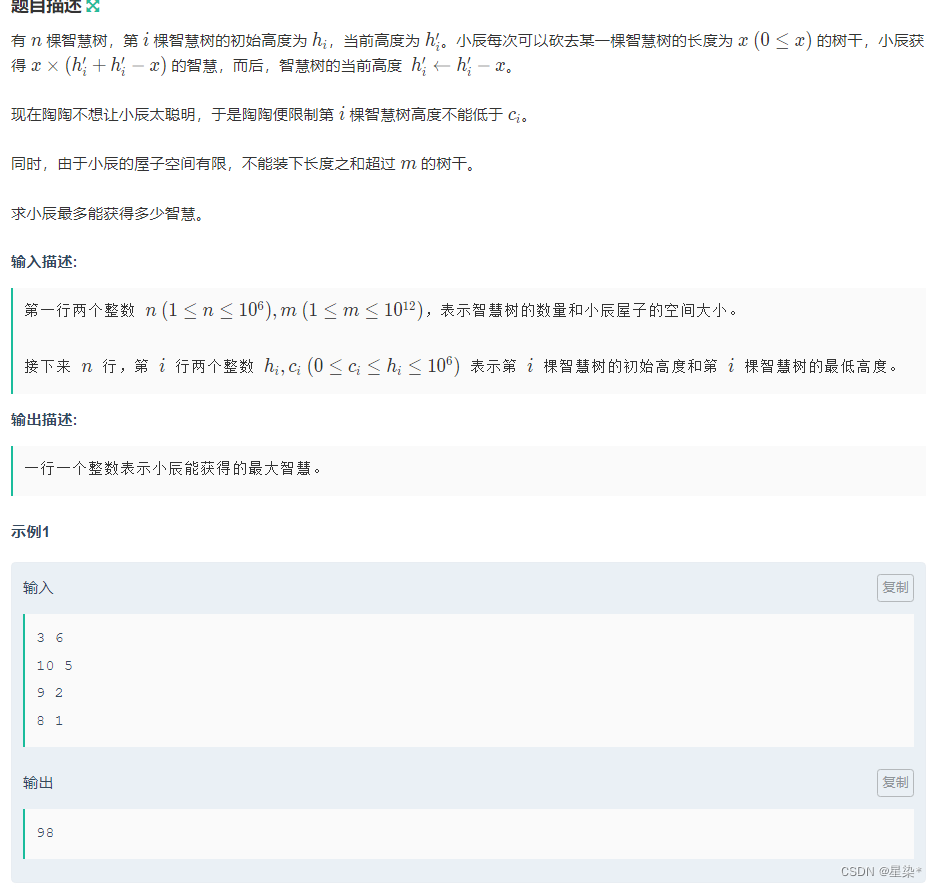
描述

输入

L=10
n=3
x={2,6,7}

输出

min=4
max=8

思路

最短时间肯定是每只蚂蚁都朝离自己最近的端点去爬行，这样不会出现蚂蚁相遇的情况

最长时间肯定是每只蚂蚁都朝离自己最远的端点去爬行，但这样会发生蚂蚁相遇的情况

对于最长时间中相遇情况的分析

我们先假设竿子左右两端记为A、B，假设竿子总长度记为Lcm，两只蚂蚁到左端的距离分别为x1cm、x2cm（蚂蚁1在竿子中间左处，蚂蚁2在竿子中间右处）

由题意知每只蚂蚁的运动速度为每秒1cm，而对于蚂蚁1最长时间为L-x1，对于蚂蚁2最长时间为x2

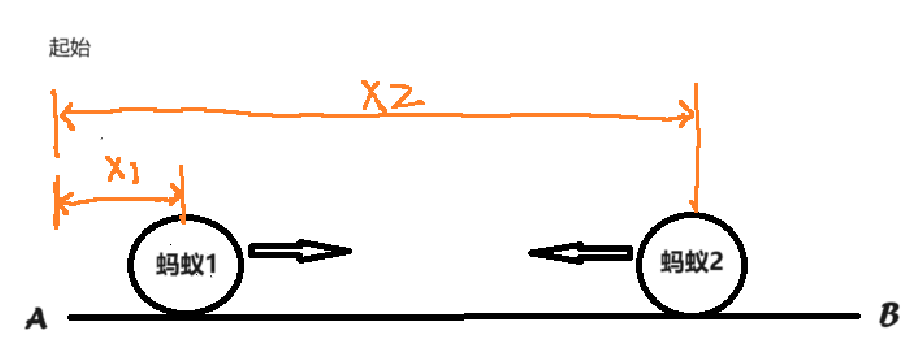
图1

蚂蚁走啊走啊走 相遇了这时候怎么办（假设在相遇的瞬间蚂蚁1已经走了s1的距离，蚂蚁2已经走了s2的距离）

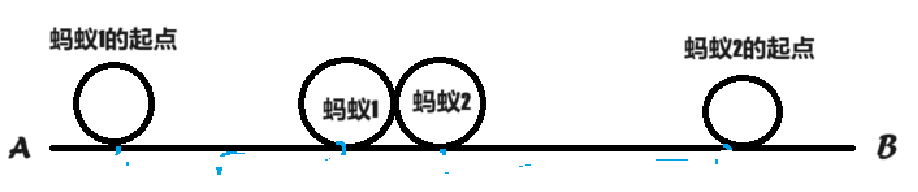
图2

这时我们假设忽略不同蚂蚁间的区别（即将蚂蚁1当做蚂蚁2,让蚂蚁1调头向左爬行，直至端点A，将蚂蚁2当做蚂蚁1,让蚂蚁2调头向右爬行，直至端点B，那么两只蚂蚁的最长时间问题就迎刃而解了）读到这相信大家应该都能听懂了我匮乏的语言描述了吧

code

int L,n;
int x[10000];//存储每只蚂蚁到左端的距离
void solve()
{//计算最短时间int min_t=0;for(int i=0;i<n;i++){min_t=max(min_t,min(x[i],L-x[i]));//不能将max换成min，否则min_t就没有任何改变，一直都为0}//计算最长时间int max_t=0;for(int i=0;i<n;i++){max_t=max(max_t,max(x[i],L-x[i]));}printf("%d %d\n",min_t,max_t);
}