1. 二叉排序树BST
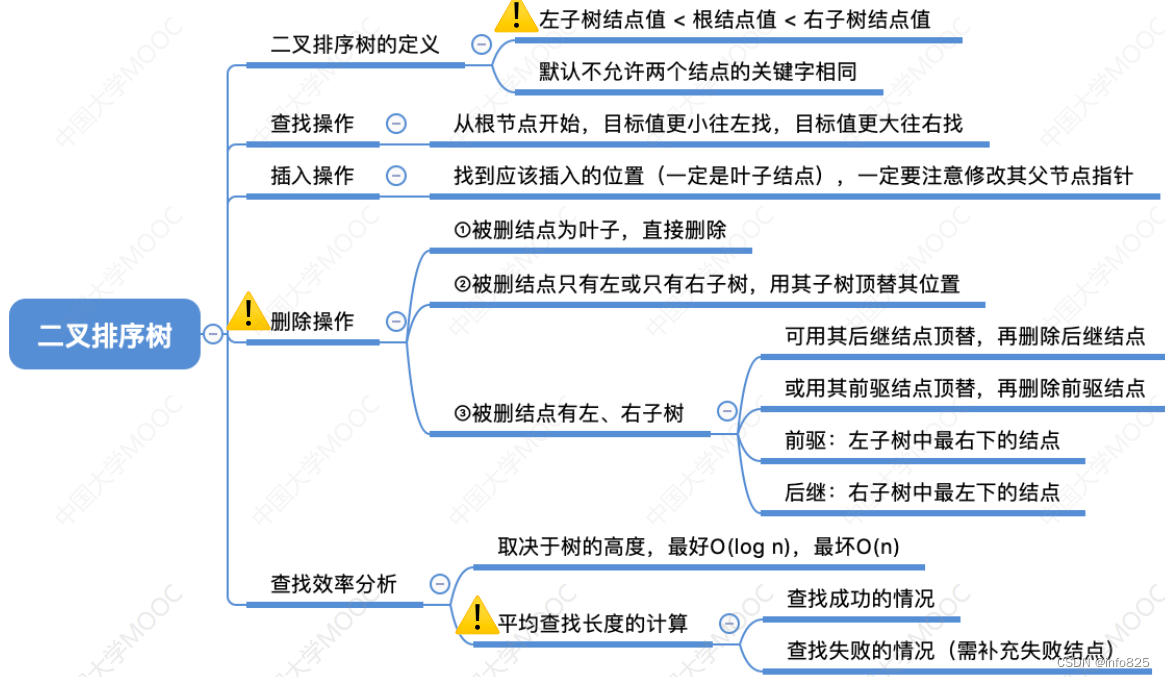
1.1 二叉排序树的定义
二叉排序树,又称二叉查找树(BST,Binary Search Tree)
一棵二叉树或者是空二叉树,或者是具有如下性质的二叉树:
- 左子树上所有结点的关键字均小于根结点的关键字;
- 右子树上所有结点的关键字均大于根结点的关键字。
- 左子树和右子树又各是一棵二叉排序树。
左子树结点值 < 根结点值 < 右子树结点值 , 进行中序遍历,可以得到一个递增的有序序列
适用范围: 二叉排序树可用于元素的有序组织、搜索
1.2 二叉排序树的查找
1.2.1 算法流程
若树非空,目标值与根结点的值比较;
4. 若相等,则查找成功;
5. 若小于根结点,则在左子树上查找;
6. 否则在右子树上查找;
查找成功,返回结点指针;查找失败返回NULL 。
1.2.2 代码实现
typedef struct BSTNode{int key;struct BSTNode *lchild, *rchild;
}BSTNode, *BSTree;//在二叉排序树中查找值为key的结点(非递归)
//最坏空间复杂度:O(1)
BSTNode *BST_Search(BSTree T, int key){while(T!=NULL && key!=T->key){ //若树空或等于跟结点值,则结束循环if(key<T->key) //值小于根结点值,在左子树上查找T = T->lchild;else //值大于根结点值,在右子树上查找T = T->rchild;}return T;
}//在二叉排序树中查找值为key的结点(递归)
//最坏空间复杂度:O(h)
BSTNode *BSTSearch(BSTree T, int key){if(T == NULL)return NULL;if(Kry == T->key)return T;else if(key < T->key)return BSTSearch(T->lchild, key);else return BSTSearch(T->rchild, key);
}
1.3 二叉排序树的插入操作
1.3.1 算法流程
- 若原二叉排序树为空,则直接插入结点;否则;
- 若关键字k小于根结点值,则递归插入到左子树;
- 若关键字k大于根结点值,则递归插入到右子树。
最坏空间复杂度:O(h)
1.3.2 代码实现
//在二叉排序树中插入关键字为k的新结点(递归)
//最坏空间复杂度:O(h)
int BST_Insert(BSTree &T, int k){if(T==NULL){ //原树为空,新插入的结点为根结点T = (BSTree)malloc(sizeof(BSTNode));T->key = k;T->lchild = T->rchild = NULL;return 1; //插入成功}else if(K == T->key) //树中存在相同关键字的结点,插入失败return 0;else if(k < T->key) return BST_Insert(T->lchild,k);else return BST_Insert(T->rchild,k);
}
1.4 二叉排序树的构造
依次将每个关键字插入到二叉排序树中(不同的关键字序列可能得到同款二叉排序树,也可能得到不同款二叉排序树)
//按照str[]中的关键字序列建立二叉排序树
void Crear_BST(BSTree &T, int str[], int n){T = NULL; //初始时T为空树int i=0;while(i<n){BST_Insert(T,str[i]); //依次将每个关键字插入到二叉排序树中i++;}
}
1.5 二叉排序树的删除
1.5.1 算法流程
先搜索找到目标结点:
- 若被删除结点z是叶结点则直接删除,不会破坏二叉排序树的性质;
- 若结点z只有一棵左子树或右子树,则让z的子树成为z父结点的子树,替代z的位置;
- 若结点z有左、右两棵子树,则令z的直接后继 (或直接前驱) 替代z,然后从二叉排序树中删去这个直接后继(或直接前驱),这样就转换成了第一或第二种情况。
- z的后继:z的右子树中最左下结点(该节点一定没有左子树)=347x240)
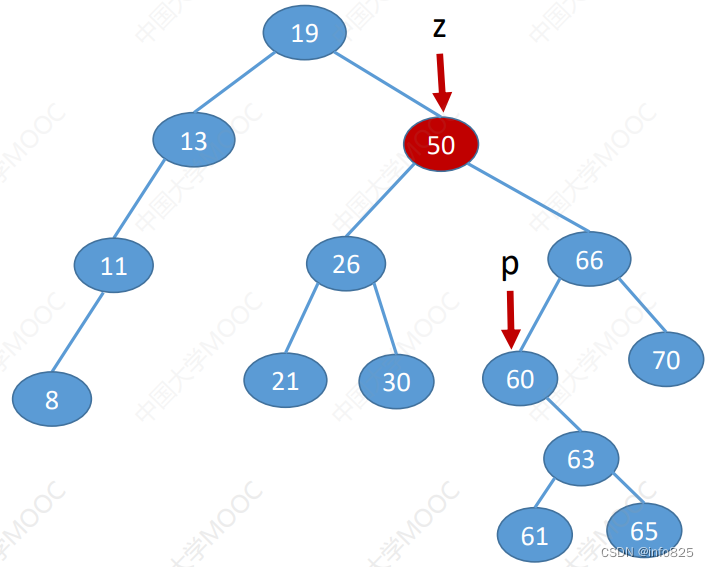
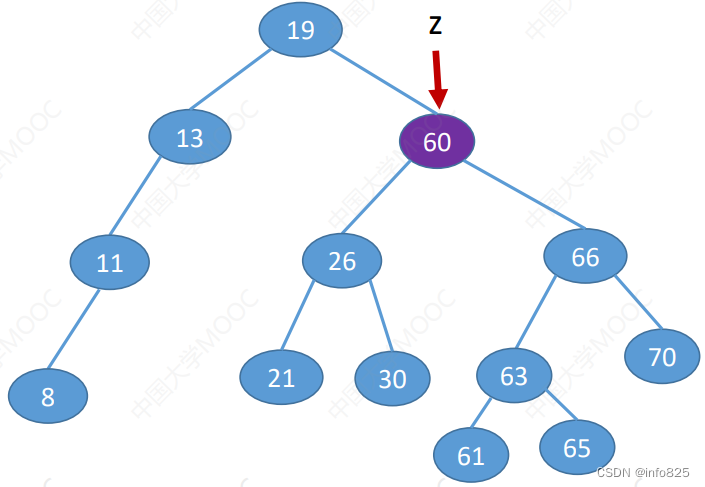
- z的前驱:z的左子树中最右下结点(该节点一定没有右子树)
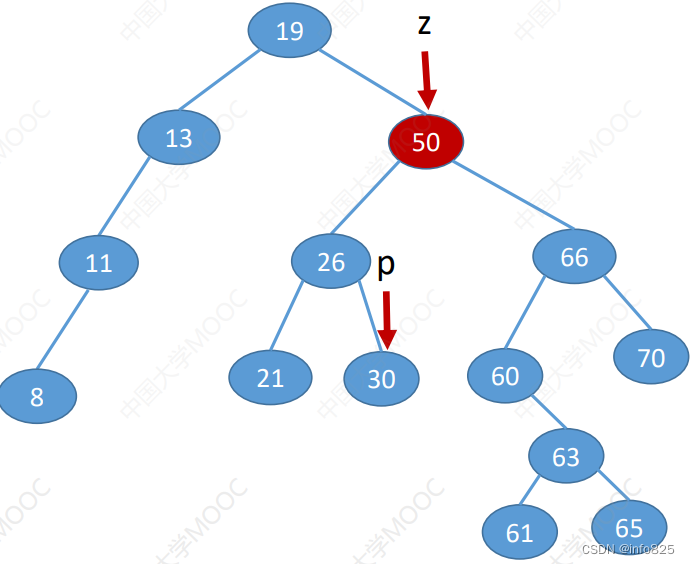
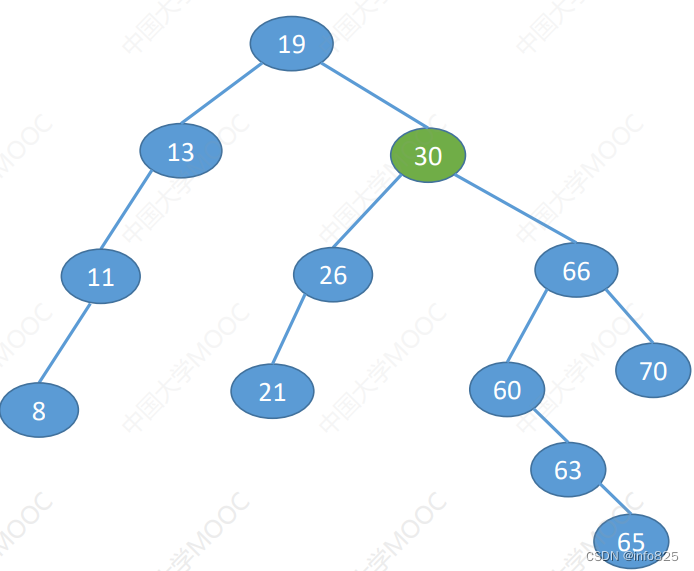
1.6 查找效率分析
查找长度: 在查找运算中,需要对比关键字的次数称为查找长度,反映了查找操作时间复杂度
- 若树高h,找到最下层的一个结点需要对比 h 次.
- 最好情况:n个结点的二叉树最小高度为 ⌊ log 2 n ⌋ + 1 \left \lfloor \log_{2}n \right \rfloor+1 ⌊log2n⌋+1。平均查找长度= O( log 2 n \log_{2}n log2n。
- 最坏情况:每个结点只有一个分支,树高h=结点数n。平均查找长度=O(n)。
1.6.1 查找成功的情况下
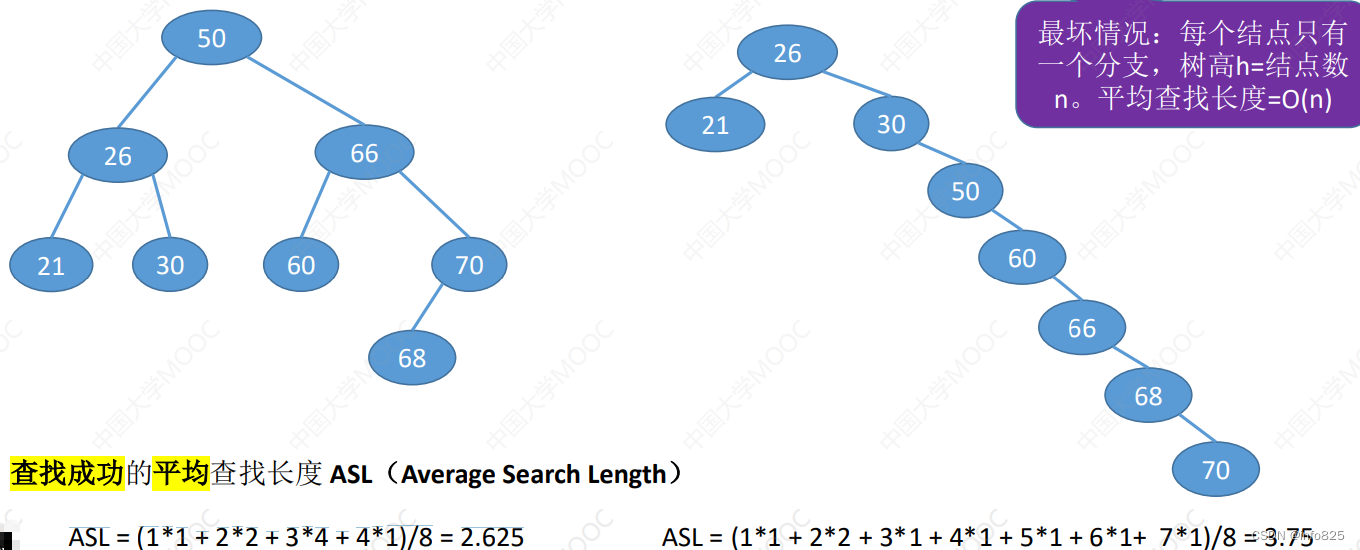
1.6.1 查找成功的情况下(需补充失败结点)
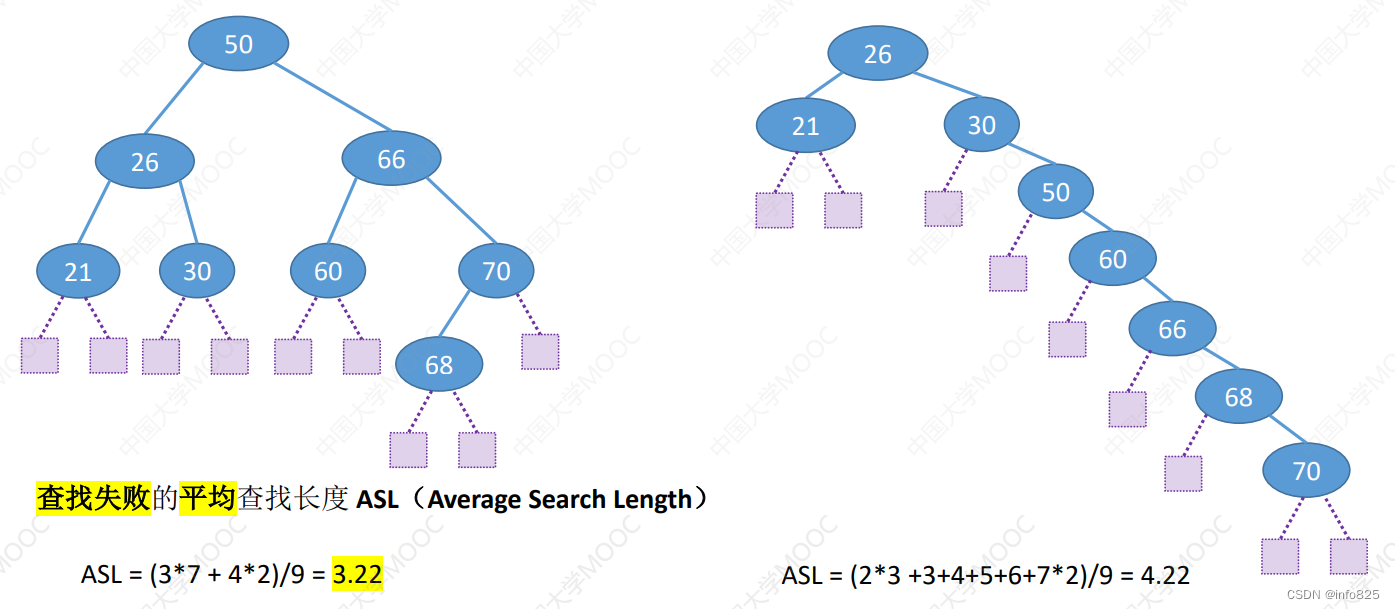
2. 平衡二叉树
2.1 基础概念
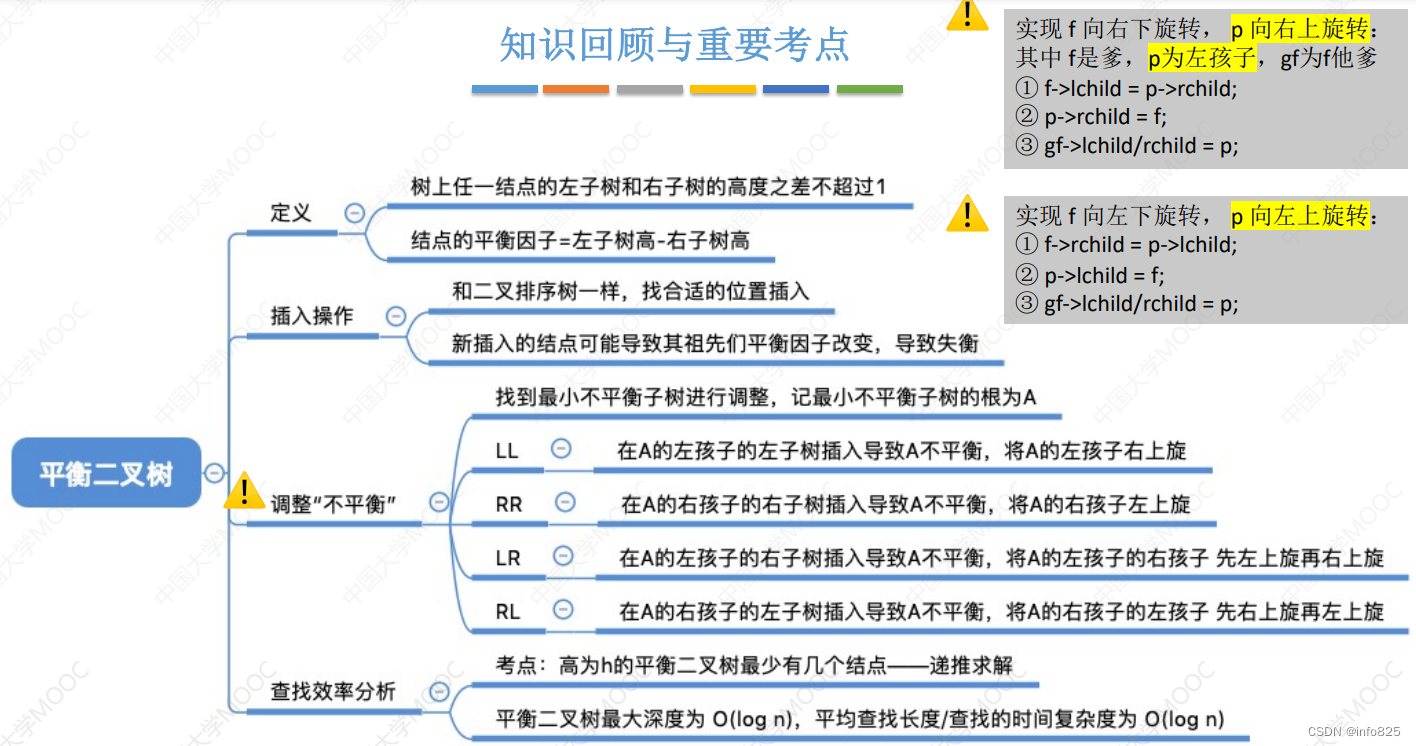
2.1.1 定义
平衡二叉树(Balanced Binary Tree),简称平衡树(AVL树,G. M. Adelson-Velsky和E. M. Landis))——树上任一结点的左子树和右子树的高度之差不超过1。
结点的平衡因子=左子树高-右子树高。
- 平衡二叉树结点的平衡因子的值只可能是−1、0或1
- 只要有任一结点的平衡因子绝对值大于1,就不是平衡二叉树
2.1.2 结点代码实现
//平衡二叉树结点
typedef struct AVLNode{int key; //数据域int balance; //平衡因子struct AVLNode *lchild; *rchild;
}AVLNode, *AVLTree;
2.2 平衡二叉树的插入
2.2.1 过程分析
在插入操作中,只要将最小不平衡子树调整平衡,则其他祖先结点都会恢复平衡。

2.2.2 调整最小不平衡子树(四种情况)

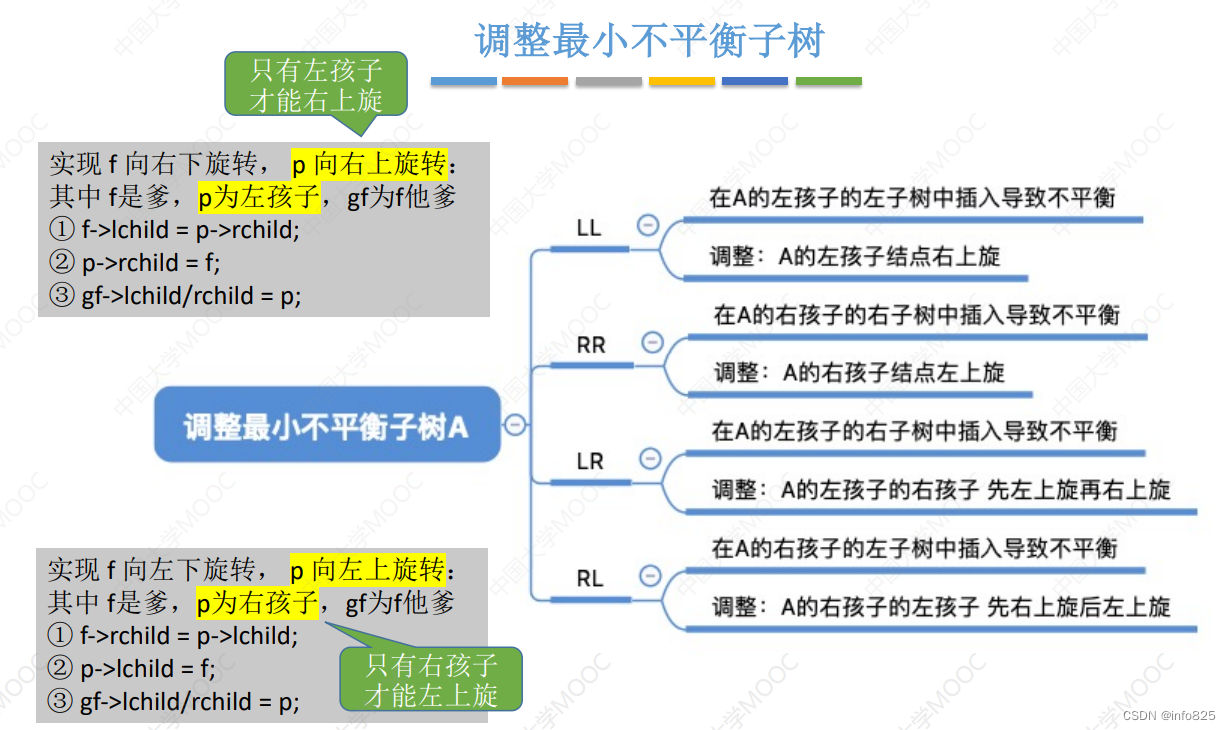
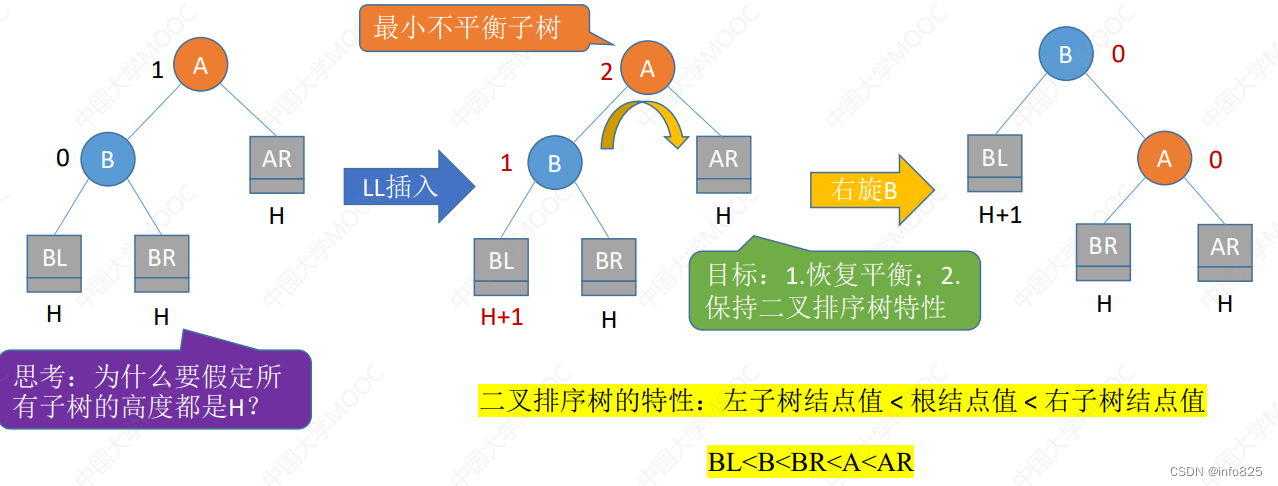
- 调整最小不平衡子树(LL)
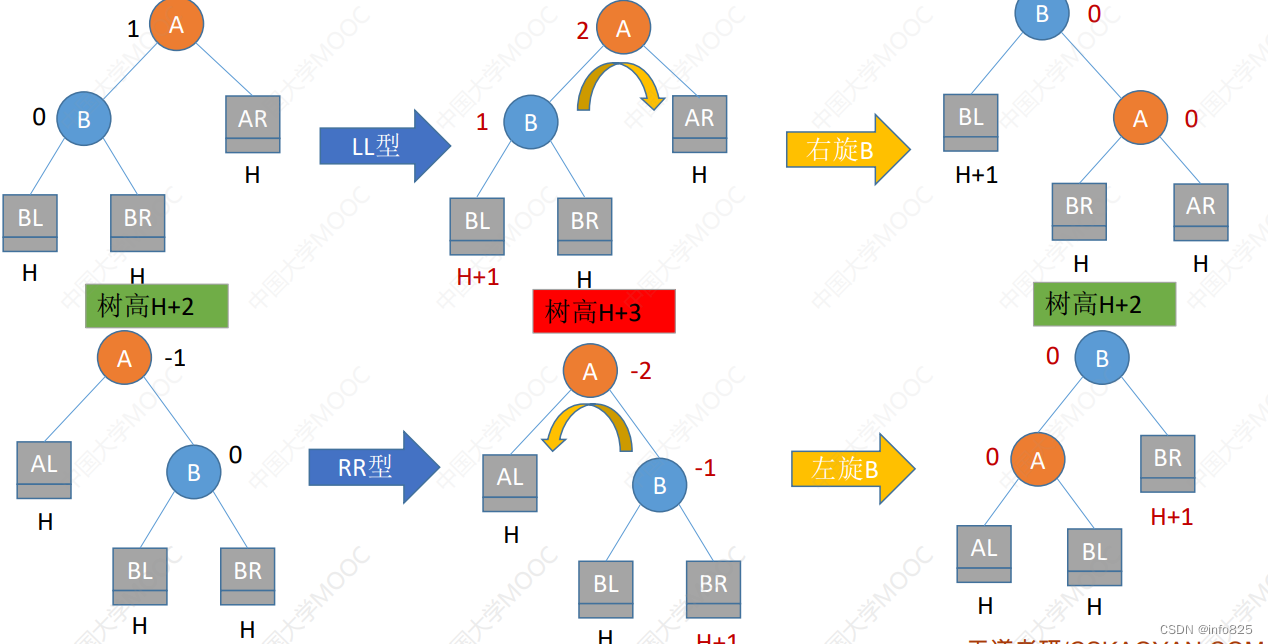
LL平衡旋转(右单旋转)。由于在结点A的左孩子(L)的左子树(L)上插入了新结点,A的平衡因子由1增至2,导致以A为根的子树失去平衡,需要一次向右的旋转操作。将A的左孩子B向右上旋转代替A成为根结点,将A结点向右下旋转成为B的右子树的根结点,而B的原右子树则作为A结点的左子树。
- 调整最小不平衡子树(RR)
RR平衡旋转(左单旋转)。由于在结点A的右孩子(R)的右子树(R)上插入了新结点,A的平衡因子由-1减至-2,导致以A为根的子树失去平衡,需要一次向左的旋转操作。将A的右孩子B向左上旋转代替A成为根结点,将A结点向左下旋转成为B的左子树的根结点,而B的原左子树则作为A结点的右子树.
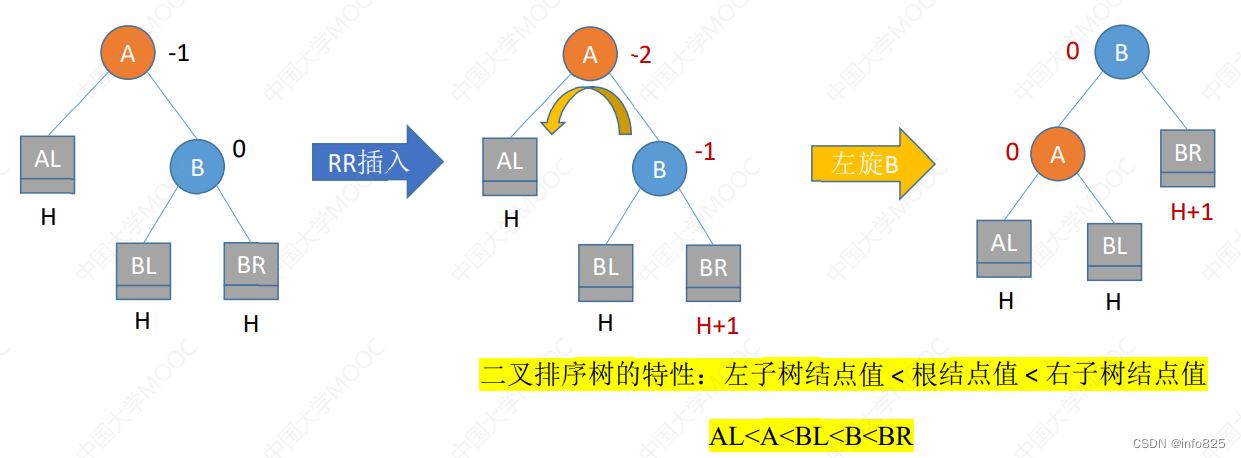
代码实现
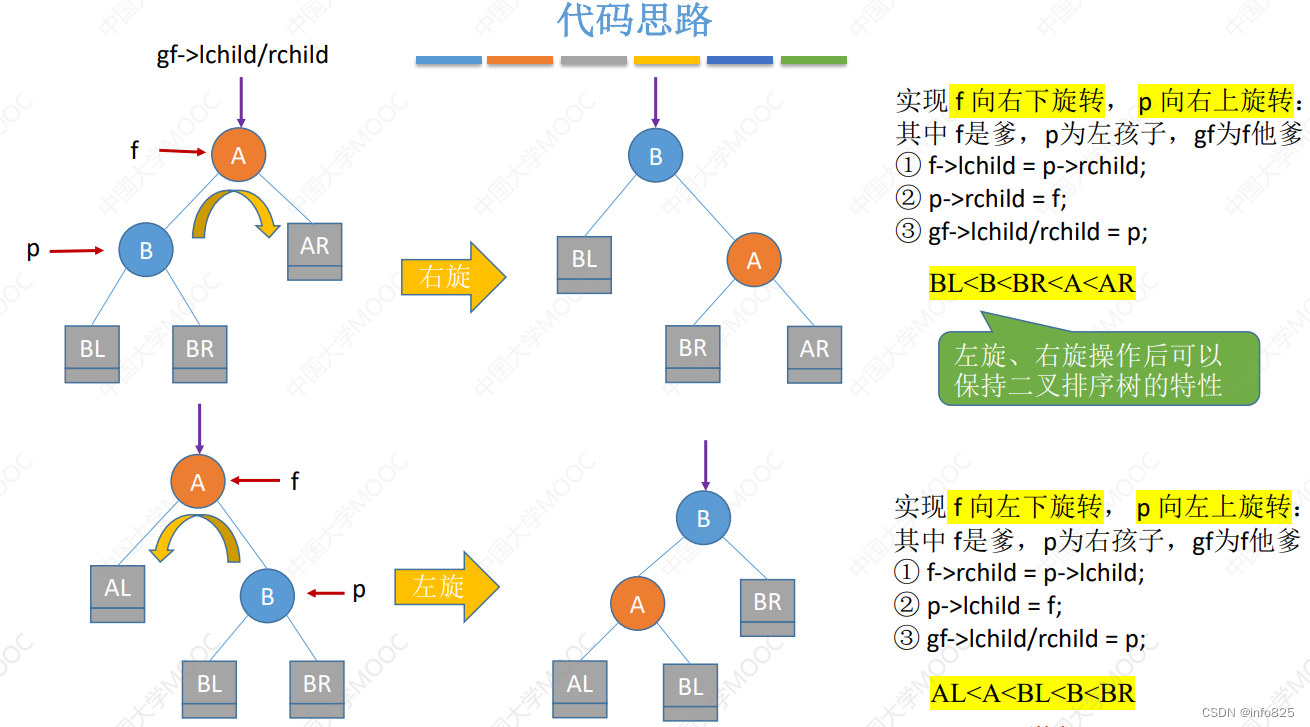
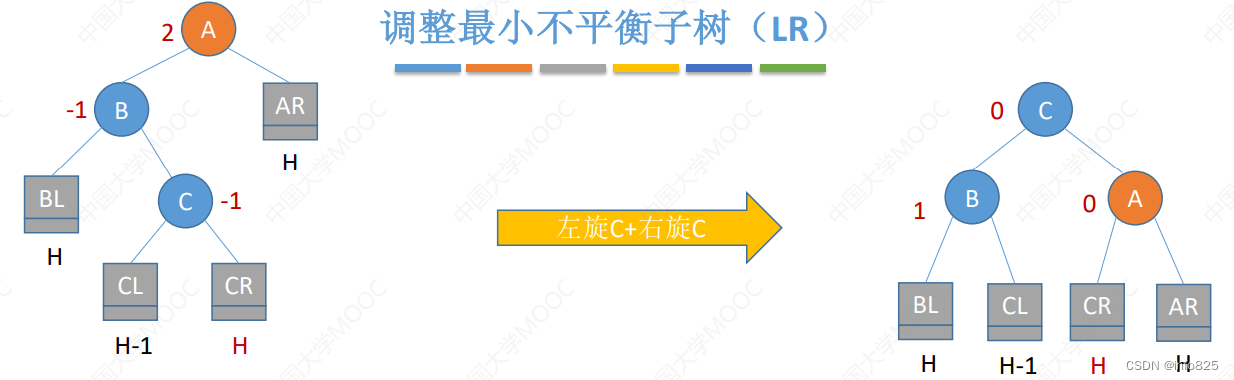
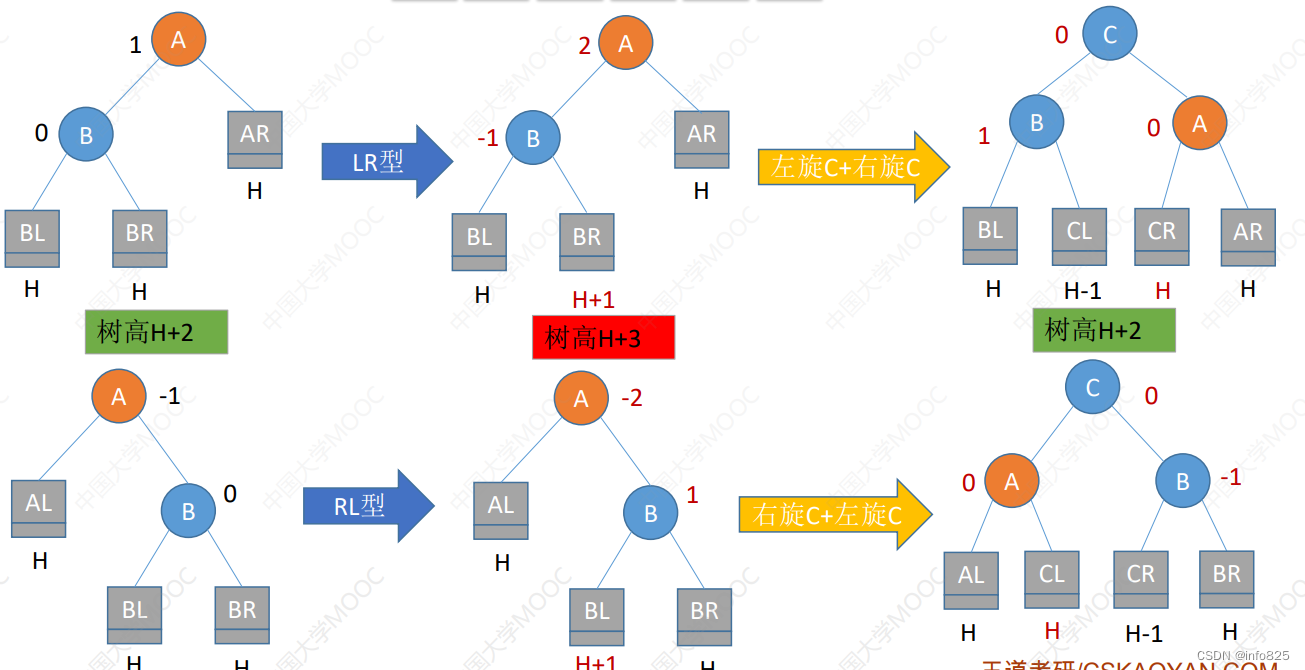
- 调整最小不平衡子树(LR):由于在 A 的左孩子(L)的右子树(R)上插入新结点,A 的平衡因子由 1 增至 2,导致以 A 为根的子树失去平衡,需要进行两次旋转操作,先左旋转后右旋转。先将 A 结点的左孩子 B 的右子树的根结点 C 向左上旋转提升到 B 结点的位置,然后再把该 C 结点向右上旋转提升到 A 结点的位置。
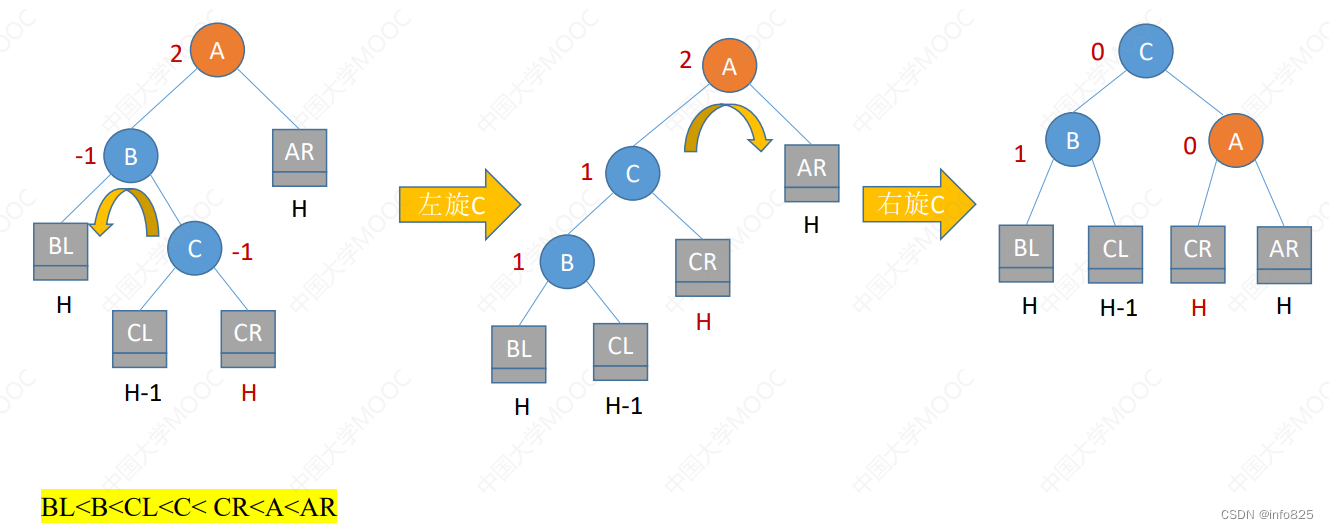
也有可能是插入到C的右子树
- 调整最小不平衡子树(RL)
由于在 A 的右孩子(R)的左子树(L)上插入新结点,A 的平衡因子由 -1 减至 -2,导致以 A 为根的子树失去平衡,需要进行两次旋转操作,先右旋转后左旋转。先将A 结点的右孩子 B的左子树的根结点 C 向右上旋转提升到 B 结点的位置,然后再把该 C 结点向左上旋转提升到 A 结点的位置。
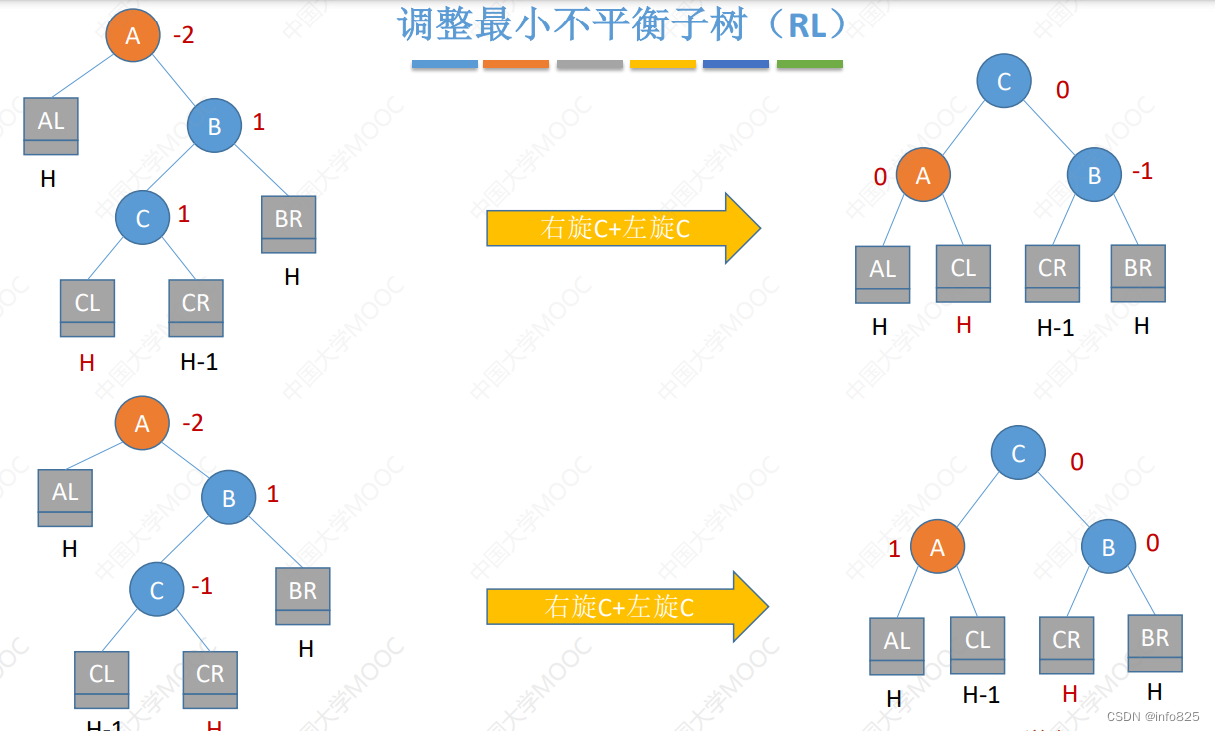
插入操作导致“最小不平衡子树”高度+1,经过调整后高度恢复,在插入操作中,只要将
最小不平衡子树调整平衡,则其他祖先结点都会恢复平衡
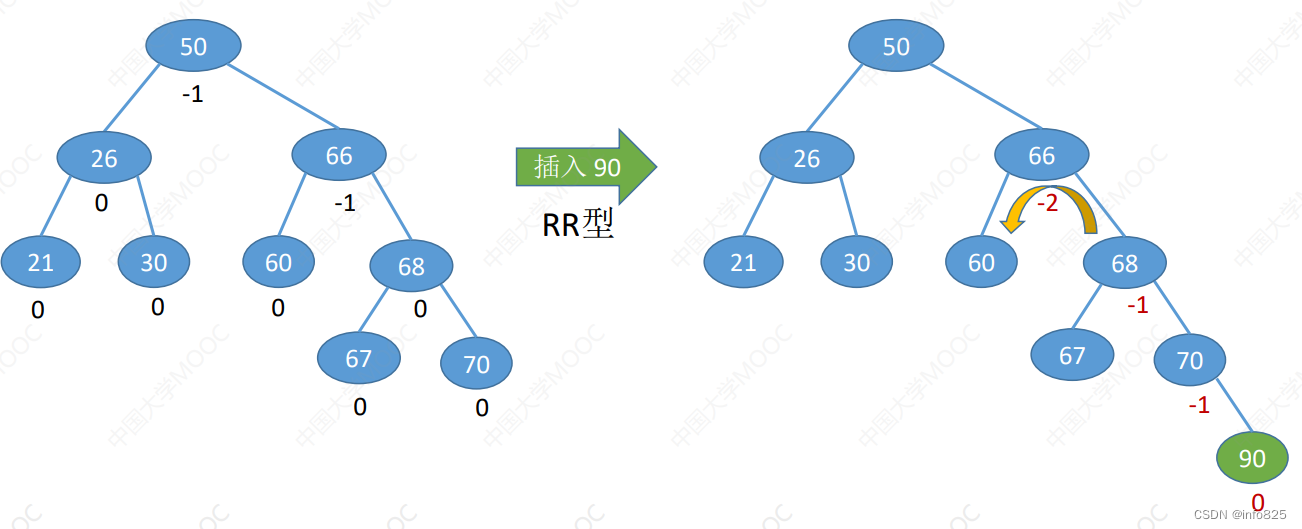
2.2.3 实战练习
- RR型
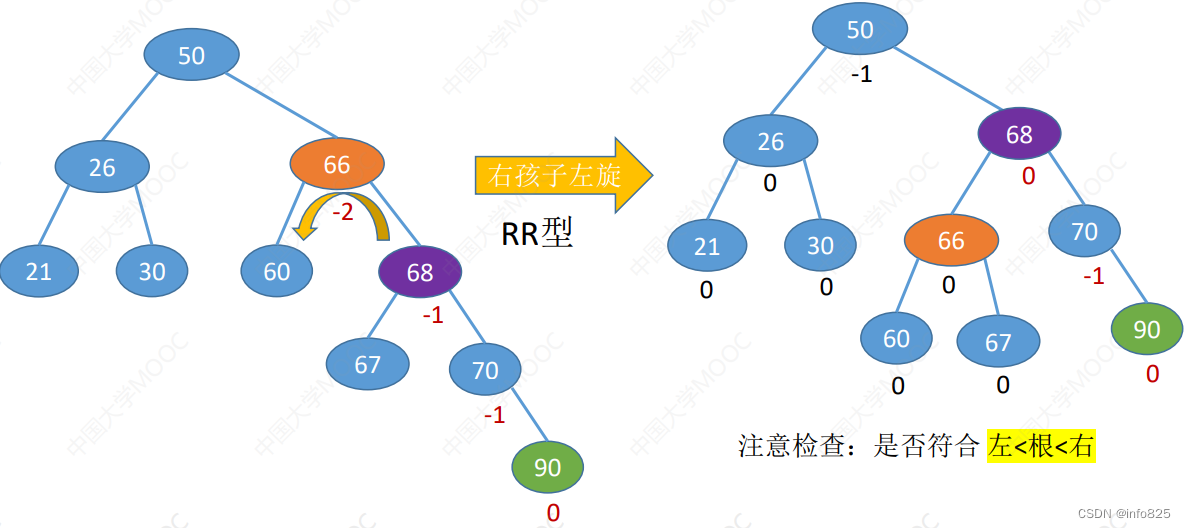
- RL型
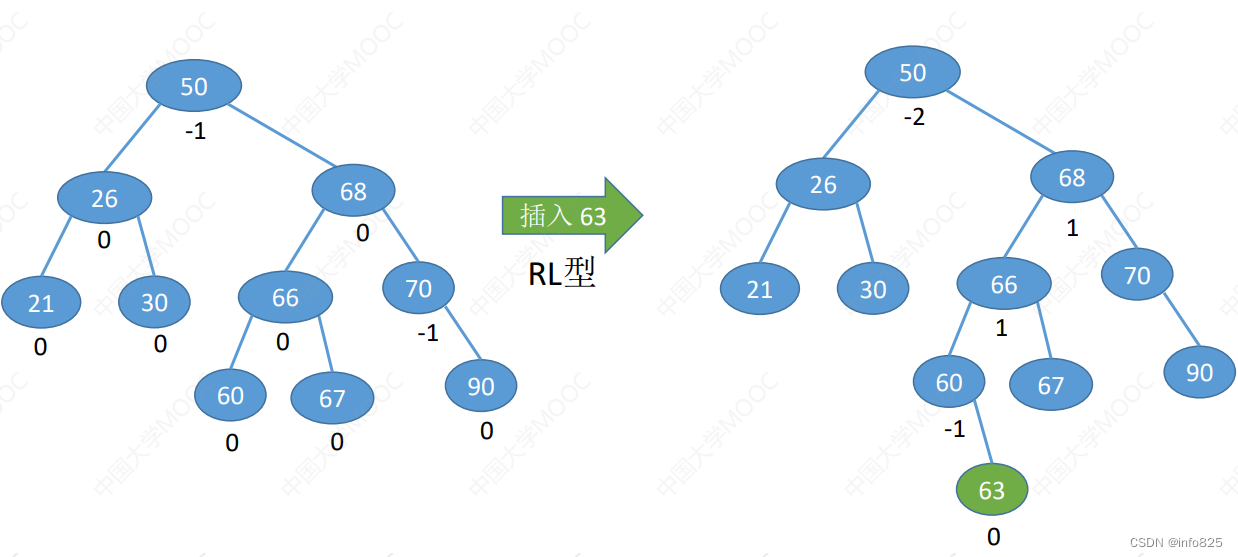
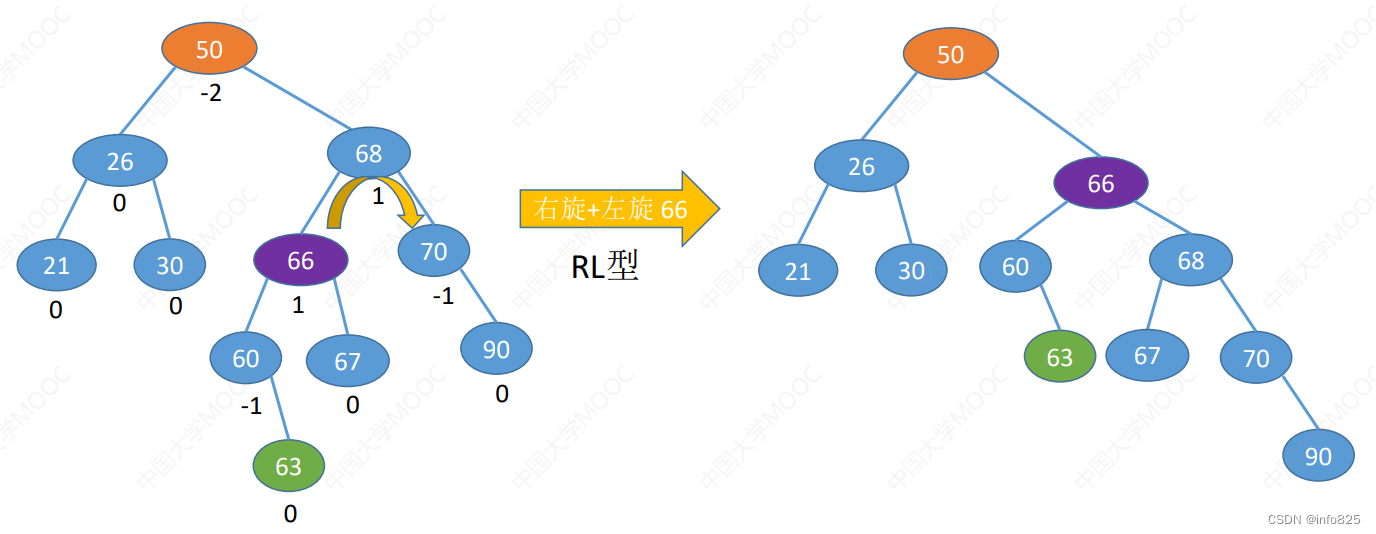
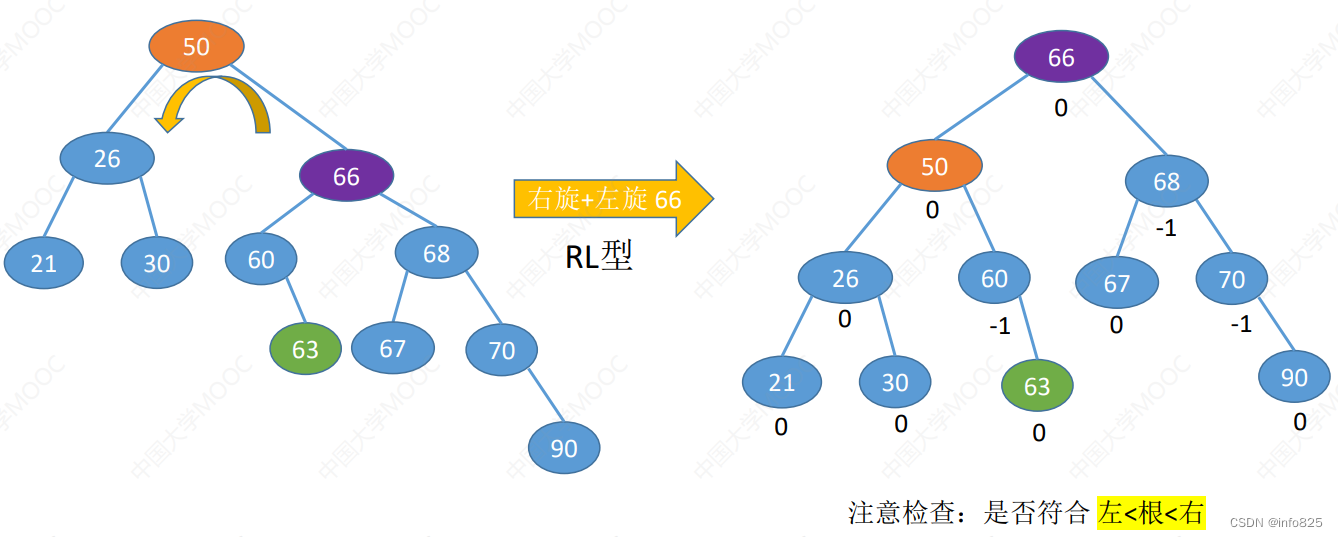
3. LR型
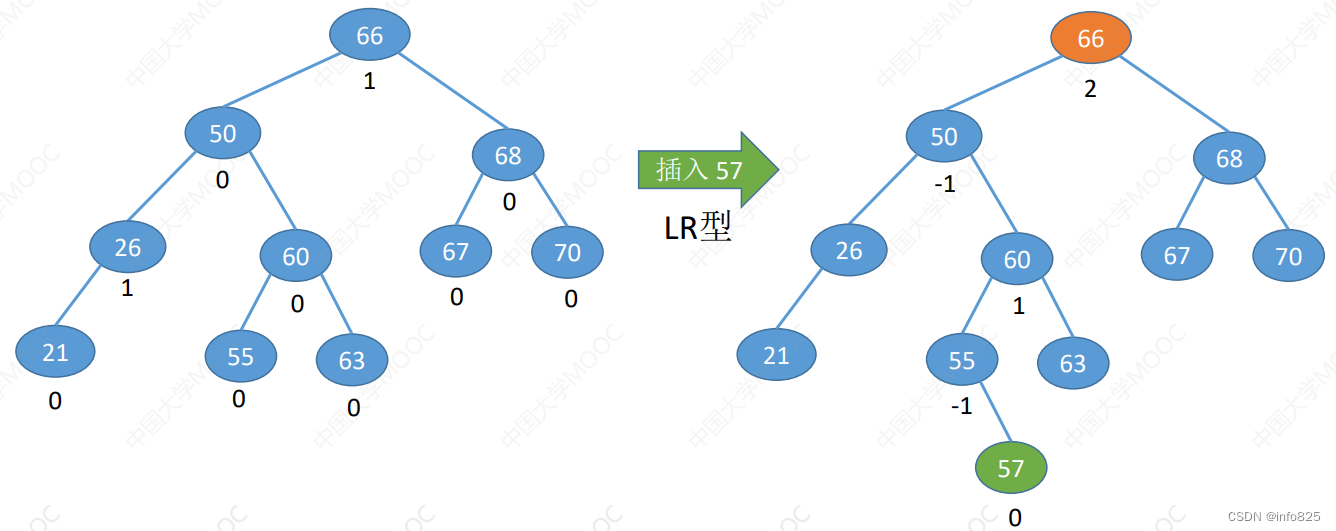
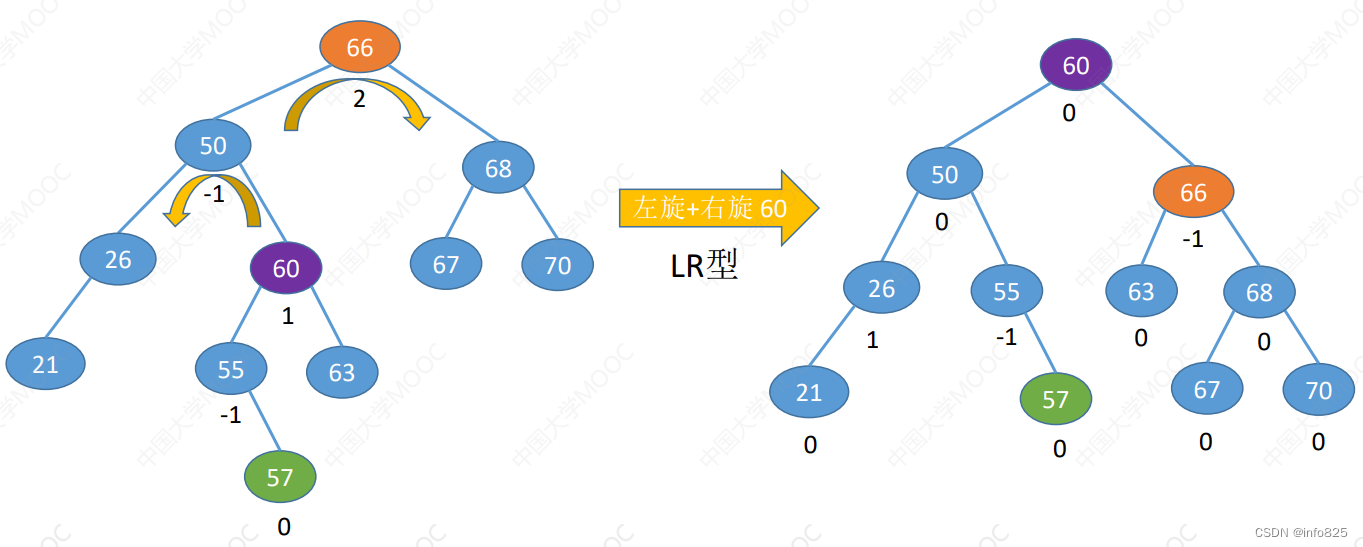
2.3 查找效率分析
若树高为h,则最坏情况下,查找一个关键字最多需要对比 h 次,即查找操作的时间复杂度不可能
超过 O(h)
![]()
平衡二叉树——树上任一结点的左子树和右子树的高度之差不超过1

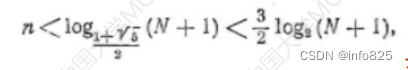
2.4 平衡二叉树的删除
2.4.1 平衡二叉树的删除操作要求:
• 删除结点后,要保持二叉排序树的特性不变(左<中<右)
• 若删除结点导致不平衡,则需要调整平衡
2.4.2 平衡二叉树的删除操作具体步骤:
①删除结点(方法同“二叉排序树”)

②一路向北找到最小不平衡子树,找不到就完结撒花
③找最小不平衡子树下,“个头”最高的儿子、孙子
④根据孙子的位置,调整平衡(LL/RR/LR/RL)
孙子在LL:儿子右单旋
• 孙子在RR:儿子左单旋
• 孙子在LR:孙子先左旋,再右旋
• 孙子在RL:孙子先右旋,再左旋
⑤如果不平衡向上传导,继续②
对最小不平衡子树的旋转可能导致树变矮,从而导致上层祖先不平衡(不平衡向上传递)
例1:
- 删除

- 找最小不平衡子树

- 找最小不平衡子树下,“个头”最高的儿子、孙子

根据孙子的位置,调整平衡(LL/RR/LR/RL)
孙子在RR:儿子左单旋

例2:
1.删除结点
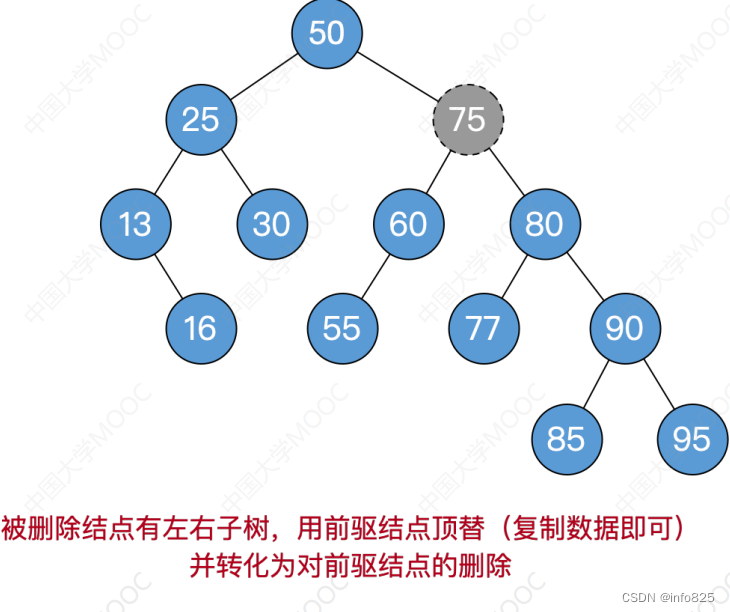


2.一路向北找到最小不平衡子树,找不到就完结撒花

3.找最小不平衡子树下,“个头”最高的儿子、孙子

4.根据孙子的位置,调整平衡(LL/RR/LR/RL)
孙子在RR:儿子左单旋

5.如果不平衡向上传导,继续②
2.4.3 删除效率
平衡二叉树删除操作时间复杂度=O( l o g 2 n log_{2}n log2n)
3. 红黑树(Red-Black Tree)RBT
3.1 为什么要发明 红黑树?
3.11 效率对比

- 如果二叉排序树完全不平衡,则其深度可达到n,查找效率为O(n),退化为顺序查找。
- 平衡二叉树 AVL:插入/删除 很容易破坏“平衡”特性,需要频繁调整树的形态。如:插入操作导致不平衡,则需要先计算平衡因子,找到最小不平衡子树(时间开销大),再进行 LL/RR/LR/RL 调整
- 红黑树 RBT:插入/删除 很多时候不会破坏“红黑”特性,无需频繁调整树的形态。即便需要调整,一般都可以在常数级时间内完成
3.1.2 适用范围
- 平衡二叉树:适用于以查为主、很少插入/删除的场景
- 红黑树:适用于频繁插入、删除的场景,实用性更强
3.2 考试考法

- 红黑树的定义、性质——选择题
- 红黑树的插入/删除——要能手绘插入过程(不太可能考代码,略复杂),删除操作也比较麻烦,也许不考
3.3 红黑树的定义
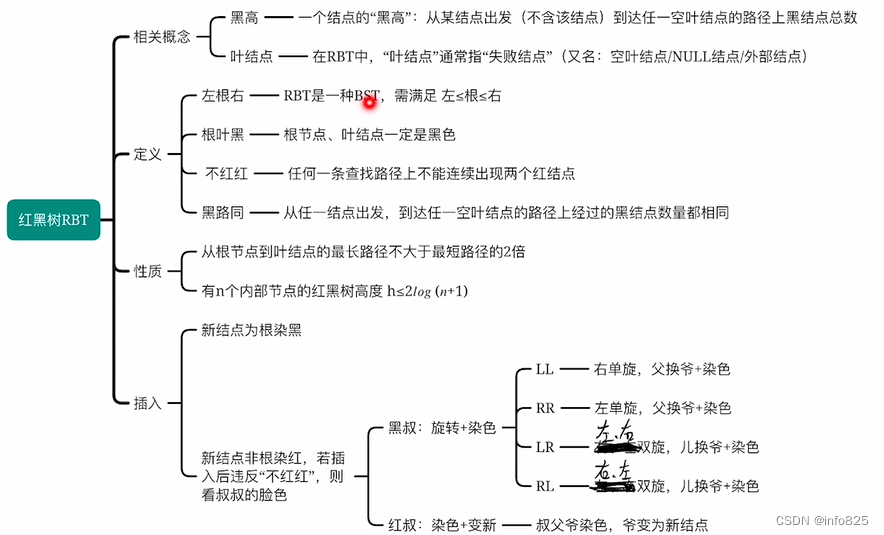
3.3.1 性质
- 必须是二叉排序树左子树结点值 ≤ 根结点值 ≤ 右子树结点值,且每个结点或是红色,或是黑色的——左根右;
- 根节点是黑色的,叶结点 (外部结点、NULL结点、失败结点) 均是黑色的——根叶黑;
- 不存在两个相邻的红结点(即红结点的父节点和孩子结点均是黑色)——不红红;
- 对每个结点,从该节点到任一叶结点的简单路径上,所含黑结点的数目相同——黑路同。
- 结点的黑高bh --从某结点出发 (不含该结点)到达任一空叶结点的路径上黑结点总数。
性质1:从根节点到叶结点的最长路径不大于最短路径的2倍。
性质2:有n个内部节点的红黑树高度 h ⩽ 2 log 2 ( n + 1 ) h\leqslant 2\log_{2}(n+1) h⩽2log2(n+1)

3.3.2 实例:

3.3.3 结点定义