LCR 079. 子集 - 力扣（LeetCode）

方法一 

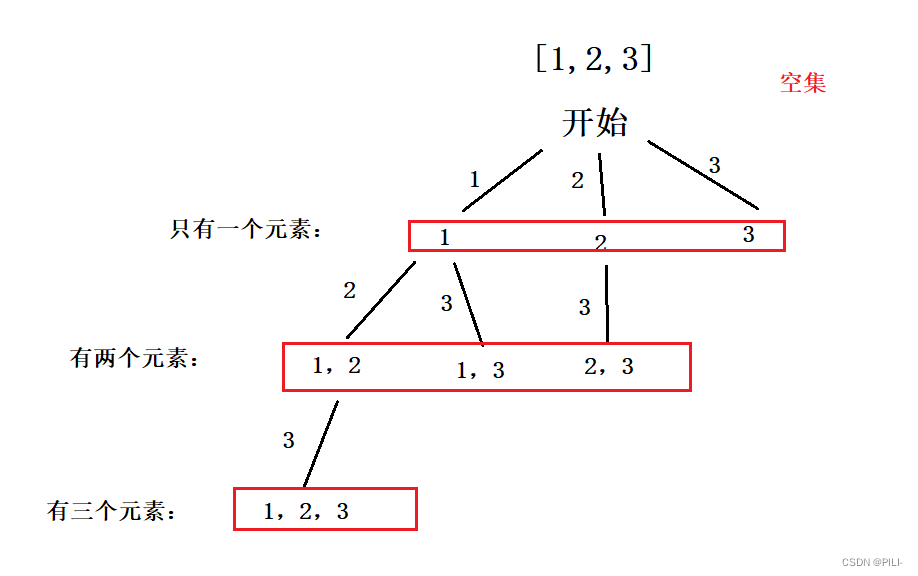
1. 决策树：对于决策树，思考的角度不同，画出的决策树也会不同，这道题可以从两个角度来画决策树。

2. 考虑全局变量的使用：

使用全局变量 List<List<Integer>> ret 来存子集；

使用全局变量 List<Integer> path 来存递归过程中的值；

3. 关注递归本身，回溯，剪枝，递归出口：

1. 递归本身：使用方法 dfs(nums，i)，nums为参数数组，i 表示当前进行选择或者不选择的目标数是 nums[i]，当选择目标数的时候，path + nums[i] 然后递归下一轮，不选择的时候，直接递归下一轮，dfs(nums，i+1)；

2. 剪枝：从决策树可以看出，这道题是不需要到剪枝环节的；

3. 回溯：当决策树中的节点对目标数进行判断完成后，需要进行 "恢复现场" 操作，也就是需要将当前的全局变量 path 的最后一个元素去掉，从而恢复现场，可以按下图来理解；

4. 递归出口：当 dfs(nums,i) 中 i 的值 == nums.size 的时候，说明已经超出数组的范围了，此时就可以返回了；

代码实现 

class Solution {List<List<Integer>> ret;List<Integer> path;public List<List<Integer>> subsets(int[] nums) {ret = new ArrayList<>();path = new ArrayList<>();dfs(nums,0);return ret;}public void dfs(int[] nums,int i){// 递归出口if(i == nums.length){ret.add(new ArrayList(path));return;}// 选path.add(nums[i]);dfs(nums,i+1);// 回溯，恢复现场path.remove(path.size()-1);// 不选dfs(nums,i+1);}
}

方法二 

 第二种决策树：这种思考方式，就是从选择多少个元素来考虑，但要求的是从数组 i 定位从小到大进行选择，在选择完前 n 个元素后，继续选择 n+1 个元素时，只能是选择当前 i 之后对应的元素，也就是数组 [1,2,3] 当选择到 2 的时候，再进行选择时，就只能选 3 了，不能选 1 ，这样是为了避免重复情况出现；

2. 全局变量的使用与第一种方法一样； 

3. 关注递归本身，回溯，剪枝，递归出口：

1. 观察决策树，可以发现每一个节点都作为子集，也就是每次进入都可以作为一个结果然后存进全局变量 ret 中；

2. dfs(nums[]，i) 此处的 i 可以理解为当前的 path 要从 i 开始进行选择；

3. 跟第一种情况相同，不需要进行剪枝；

4. 回溯也跟第一种情况相同，将最后一个元素去掉；

5. 并且要注意，在这种情况下，是没有递归出口的，因为每个节点都作为子集，在 for 循环中循环结束后就会自动返回；

代码实现 

class Solution {List<List<Integer>> ret;List<Integer> path;public List<List<Integer>> subsets(int[] nums) {ret = new ArrayList<>();path = new ArrayList<>();dfs(nums,0);return ret;}public void dfs(int[] nums,int i){// 每个节点都是子集，进入就添加到 ret 中ret.add(new ArrayList(path));for(int j=i;j<nums.length;j++){     // 从节点 i 开始path.add(nums[j]);dfs(nums,j+1);      // 回溯，恢复现场path.remove(path.size()-1);}}
}