目录

一、为什么会出现B-树？

面试题：

二、什么是B-树？

2.1、B+,B-树,B*树 导航

三、B-树的模拟实现

3.1、插入结点分析

3.1.1、根节点的分裂

3.1.2、继续插入数据，分裂子节点

3.2.3、再次插入数据，导致根节点继续向上分裂

3.2、性能分析

3.3、模拟实现B-树

四、总结

4.1、特性

小结

---

一、为什么会出现B-树？

        我们平时所知道的二叉搜索树，红黑树，AVL树，在访问一个大文件，或者是数据量比较大的时候，可能无法一次性把数据加载到内存中，而是只在树的结点中保留了指向该数据在磁盘中的位置，也就是说，真实的数据还在磁盘；我们也知道，在内存中访问数据是很快的，而在磁盘中访问数据相对就要慢很多了；

因此存在以下缺陷：

1. 树的高度比较高，查找的最坏情况是树的高度；

2. 数据量很大时，书中结点无法一次性加载到内存中，需要多次IO；（IO速度是很慢的）；

解决方案：

1. 提高IO速度；

2. 降低树的高度——多叉平衡树；

面试题：

数据存储到hashmap和存储到文件中，有什么区别？

1. 存储到文件中读取速度慢；

2. hashmap相当于在内存中存储数据，一旦断电数据就丢失了；

---

二、什么是B-树？

注意：B-树 不是“B减树”，这个"-"只是一个分隔符，没有B-树这种数据结构；

2.1、B+,B-树,B*树 导航

什么是B树之前写过一篇文章，如下：（什么是B-树，B+树，以及特性）

http://t.csdn.cn/bnlJw

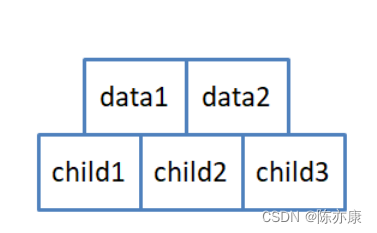
        简而言之，B树就是一颗N叉搜索树，每个结点（结点由关键字和孩子节点地址组成）中最多有N - 1，至少有N/2 - 1个关键字，这些关键字按照升序排序划分成了N个区间，孩子结点就在这些区间里，并且所有叶子结点都在同一层。

结点结构如下图：

---

三、B-树的模拟实现

3.1、插入结点分析

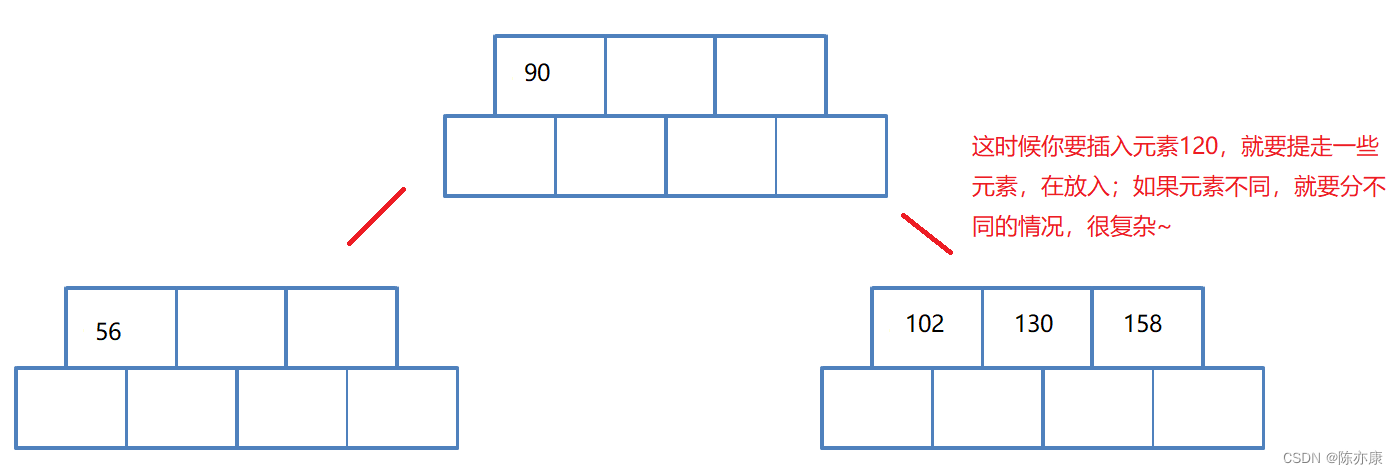
模拟实现B-树，我们通常会给每个节点多给一个空间，如下：

         为什么要多给一个空间呢？假设不多给一个空间，也就是N = 4，是一个四叉树，但是一个节点最多三个关键字，那么当你要放入第四个元素的时候，进行分裂的时候就不好分裂了，因为你要分情况，看把谁提走。如下图：（以下只是一个简略图，实际上右边树的分叉点不一定在最右边）

3.1.1、根节点的分裂

理解了上面的内容后，首先我们来看一下根节点该如何分裂~

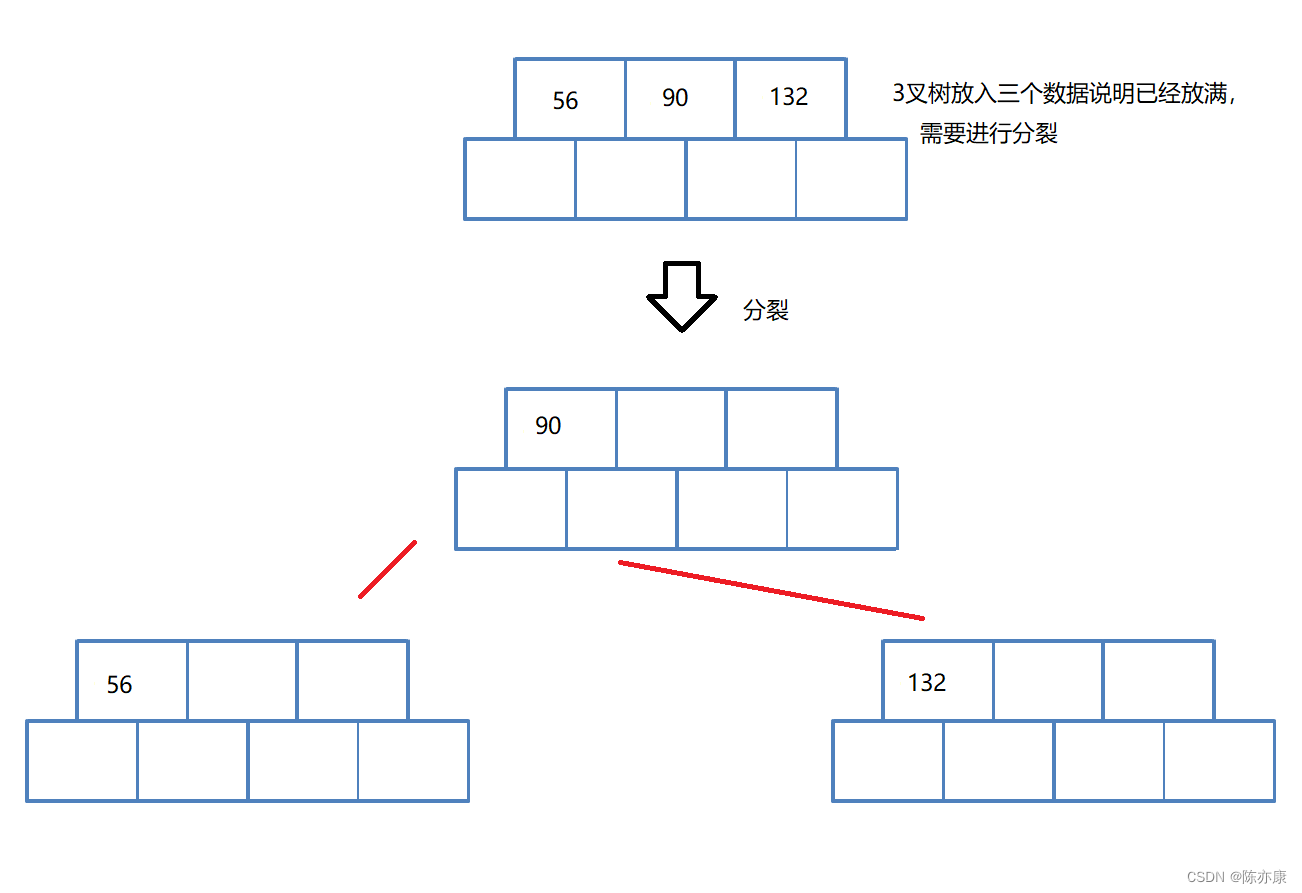
例如一个三叉树，那么刚刚说到，需要多给一个结点一个空间，也就是一个结点有三个关键字，当这个三个关键字都被填满了，就需要分裂，如何分裂呢？步骤是以下三点：

1. 找到该结点的中间位置 m；

2. m 的右边数据，存储到一个新的结点中；

3. m 这个数据，存储到一个新的结点，变成了新的根节点，对于根节点而言，原来的一个结点，被分裂成了最终的三个结点；

如下图：

3.1.2、继续插入数据，分裂子节点

这里分裂的逻辑和分裂根节点相似，具体细节会在以下图中中讲到：

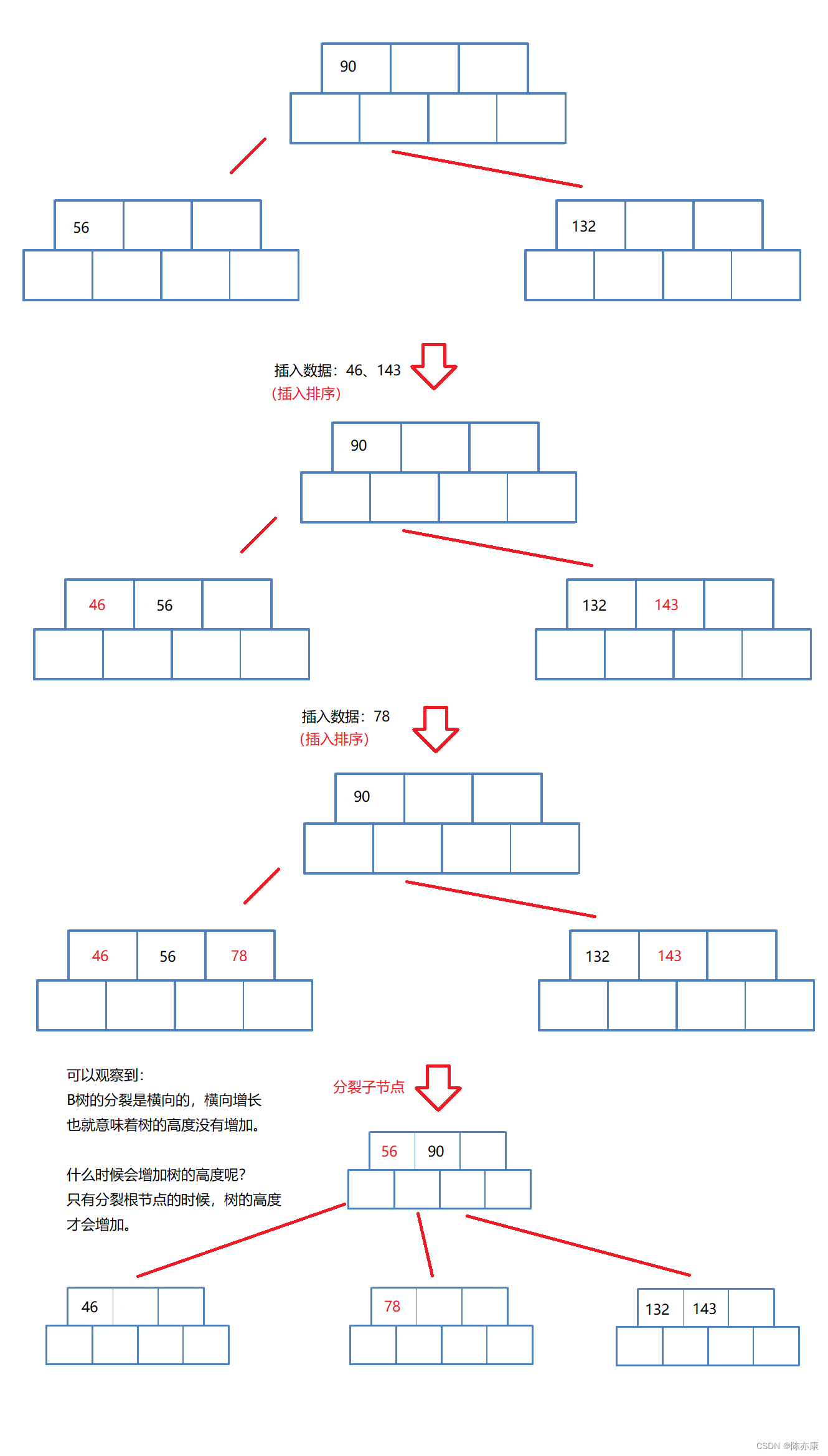
可以观察到：

B树的分裂是横向的，横向增长，也就意味着树的高度没有增加。

哪什么时候会增加树的高度呢？

只有分裂根节点的时候，树的高度才会增加。

3.2.3、再次插入数据，导致根节点继续向上分裂

        假设插入数据189，那么就会导致子节点分裂，子节点分裂又会向根节点提供一个数据，接着根节点就满了，就开始了根节点向上分裂，如下图：

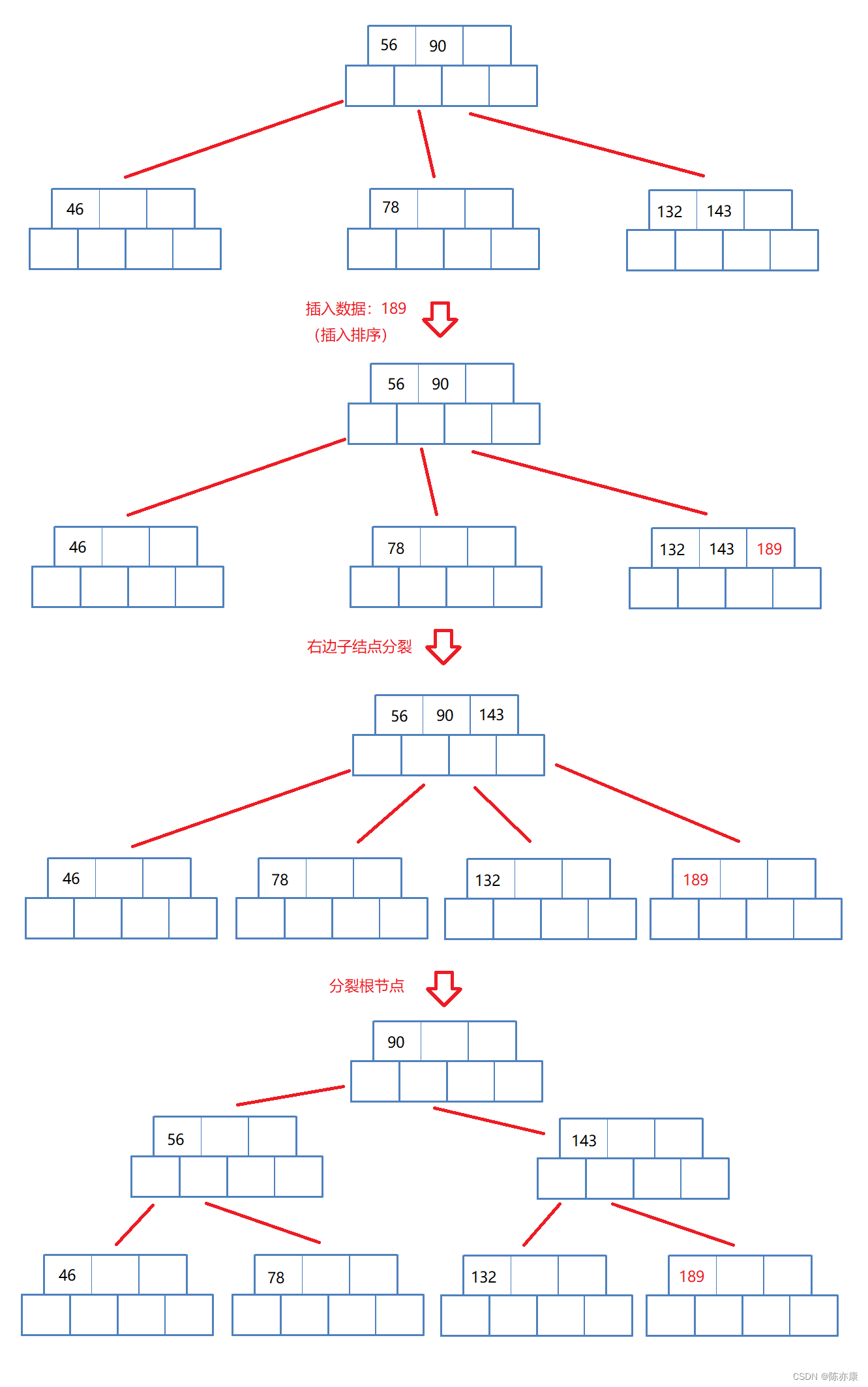
3.2、性能分析

        实际的B树不会这么平凡的分裂，一般是1024叉树，那么想象一下，当M = 1024是，插入数据时，这个树的高度会如何变化？

第一层：1023个关键字；

第二层：1024个子结点 * 1023个关键字，大约是100W的级别；

第三层：1024 * 1024 * 1023，大约是10亿的级别；

第四层：1024 * 1024 * 1024 * 1023，大约是万亿级别；

......

多么恐怖的数量，指数爆炸！！！

        那么它的时间复杂度在logM N ~ logM/2 N 之间，也就是说M越大，效率越高，但是M也不是越大越好，因为 会有空间的浪费，有因为结点满了要拷走一半，浪费一个结点一半的空间；

        并且一旦找到结点，可以利用二分查找可以快速定位到该元素，大大减少了读取磁盘的次数！！！

3.3、模拟实现B-树

具体的思路如上，详细代码和注释如下：

public class MyBtree {static class BTRNode {public int[] keys;//关键字public BTRNode[] subs;//孩子public BTRNode parent;//当前孩子节点的父亲结点public int usedSize;//当前结点关键字的数量public BTRNode() {//这里多给一个空间，是为了更好的分裂this.keys =  new int[M];this.subs = new BTRNode[M + 1];}}public static final int M = 3;public BTRNode root;//当前B树的根节点/*** 插入元素* @param key*/public boolean insert(int key) {if(root == null) {root = new BTRNode();root.keys[0] = key;root.usedSize++;return true;}//2. 当树不为空，就看Key是否存在B树中Pair<BTRNode, Integer> pair = find(key);//根据判断这里的val值是否为-1， 确定是否存在keyif(pair.getVal() != -1) {//结点存在return false;}//不存在key，就要进行插入(插入排序)BTRNode parent = pair.getKey();int index = parent.usedSize - 1;for(; index >= 0; index--) {if(parent.keys[index] >= key) {parent.keys[index + 1] = parent.keys[index];} else {break;}}parent.keys[index + 1] = key;parent.usedSize++;//为什么不处理孩子？//因为每次插入都是在叶子结点，所以叶子结点都是nullif(parent.usedSize < M) {//没有满return true;} else {//满了，需要分裂split(parent);return true;}}/*** 分裂逻辑* @param cur 代表当前需要分裂的结点*/private void split(BTRNode cur) {BTRNode newNode = new BTRNode();//1.先存储当前需要分裂结点的父节点BTRNode parent = cur.parent;//2.开始挪动数据int mid = cur.usedSize >> 1;int i = mid + 1;int j = 0;for(; i < cur.usedSize; i++) {//这里既要拷贝数值也需要拷贝孩子的地址newNode.keys[j] = cur.keys[i];newNode.subs[j] = cur.subs[i];//处理刚刚拷贝过来的孩子节点的父亲结点，为新分裂的结点if(newNode.subs[j] != null){newNode.subs[j].parent = newNode;}j++;}//多拷贝一次孩子newNode.subs[j] = cur.subs[i];if(newNode.subs[j] != null){newNode.subs[j].parent = newNode;}//更新当前新节点的有效数据newNode.usedSize = j;//这里-1是因为将来要提到父亲结点的keycur.usedSize = cur.usedSize - j - 1;//处理根节点的情况if(cur == root) {root = new BTRNode();root.keys[0] = cur.keys[mid];root.subs[0] = cur;root.subs[1] = newNode;root.usedSize = 1;cur.parent = root;newNode.parent = root;return;}//让新的结点的父亲指向刚刚分裂结点的父亲newNode.parent = parent;//开始移动父亲结点int endT = parent.usedSize - 1;int midVal = cur.keys[mid];for(; endT >= 0; endT--) {if(parent.keys[endT] >= midVal) {parent.keys[endT + 1] = parent.keys[endT];parent.subs[endT + 2] = parent.subs[endT + 1];} else {break;}}parent.keys[endT + 1] = midVal;//将当前父亲结点的孩子结点新增为newNode;parent.subs[endT + 2] = newNode;parent.usedSize++;if(parent.usedSize >= M) {split(parent);}}/*** 返回一个值是否可行？* 地址-》无法记录你存储在哪* 所以需要返回一对* @param key* @return*/private Pair<BTRNode, Integer> find(int key) {BTRNode cur = root;BTRNode parent = null;while(cur != null) {int i = 0;while(i < cur.usedSize) {if(cur.keys[i] == key) {//返回一个当前找到的结点 和 当前结点的下标return new Pair<>(cur, i);} else if(cur.keys[i] < key) {i++;} else {break;}}parent = cur;cur = cur.subs[i];}return new Pair<>(parent, -1);}//测试public static void main(String[] args) {MyBtree myBtree = new MyBtree();int[] arr = {53, 139, 75, 49, 145, 36, 101};for(int i = 0; i < arr.length; i++) {myBtree.insert(arr[i]);}System.out.println("123121");}
}

---

四、总结

4.1、特性

1. 根节点至少有两个孩子。

2. 每个非根节点至少有M/2-1(上取整)个关键字,至多有M-1个关键字，并且以升序排列。

3. 每个非根节点至少有M/2(上取整)个孩子,至多有M个孩子。

4. key[i]和key[i+1]之间的孩子节点的值介于key[i]、key[i+1]之间。

5. 所有的叶子节点都在同一层。

---

小结

面试不会考这样的，但是建议多敲~

思想要懂！

---