之前是考试准备,所以有几天没更新,今天开始继续更新
目录
快速幂模板
题目:麦森数
思路:
题目:青蛙跳
思路:
快速幂模板
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll a,b,p;
ll pow_fast(ll a,ll b,ll p){//快速幂模板(a是每个乘的底数,b是次数,p是mod)ll res=1;a%=p;while(b){//b减少,a翻倍,res存结果,p取模if(b&1) res=(res*a)%p; //奇数的时候要提前拆出来一个1,然后放心除2a=(a*a)%p;b>>=1;}return res%p;
}
int main(){cin>>a>>b>>p;cout<<a<<"^"<<b<<" mod "<<p<<"="<<pow_fast(a,b,p)<<endl;
}
题目:麦森数

思路:
思想是不变的,只不过没法直接存数据了,那么就用数组存吧,开个a存结果,b存翻倍的底数,该乘乘该加加,没了。
注意一下求位数:2^p=10^x,当然x=p*log10(2.0)+1
#include<bits/stdc++.h>
const long long mod=10000000000;
using namespace std;
const int N=2001;
int P, la=1,lb=1;//la是结果位数,lb是底数位数
int a[N],b[N],c[N];//a是结果,b是底数
void cheng1() {memset(c,0,sizeof(c));for (int i=1; i<=la; ++i) {for (int j=1; j<=lb; ++j) {c[i+j-1] += a[i]*b[j]; //高精度的乘法规则c[i+j] += (c[i+j-1])/10;c[i+j-1] %= 10;}}int lc = la+lb; //高精度乘法的长度规则while(c[lc] == 0) --lc;//lc指向有效位memcpy(a,c,sizeof(c)); //三个参数:目标地址,源地址,数据长度la=lc>500?500:lc;
}
void cheng2() {memset(c,0,sizeof(c));for (int i=1; i<=lb; ++i) {for (int j=1; j<=lb; ++j) {c[i+j-1] += b[i]*b[j];c[i+j] += (c[i+j-1])/10;c[i+j-1] %= 10;}}int lc = lb+lb;while(c[lc] == 0) --lc;memcpy(b,c,sizeof(c));lb=lc>500?500:lc;
}void pow_fast() {while(P){if(P&1) cheng1();//拆出多余的1,结果a多乘一次底数bP>>=1;cheng2();//底数b平方}
}int main() {scanf("%d",&P);printf("%d\n",int (P*log10(2.0)+1)); //求位数a[1] = 1; b[1] = 2;pow_fast();--a[1]; //2^p-1不要忘了还有减一呢for (int i = 500; i >= 1; --i) {printf("%d",a[i]);//输出结果if (!((i-1)%50)) printf("\n");}return 0;
}
题目:青蛙跳
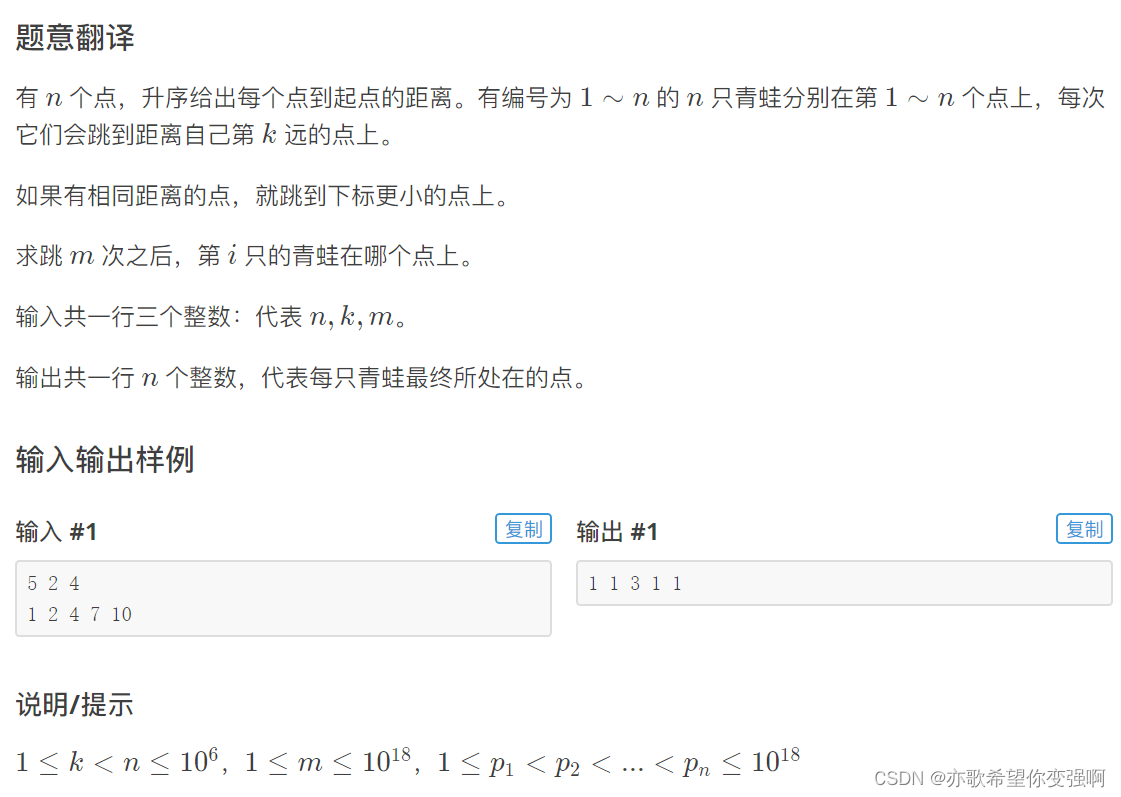
思路:
题意:有编号为1~n的 n只青蛙分别在第1~n点上,每次它们会跳到距离自己第 k近的点上。然后跳m次!
我尼玛这么大的数据咋做呀
首先我们要解决每个点第一次跳的地方,注意到k的范围,额,别想着暴力了。
引入滑动窗口(以后讲),把最优的决策放左边(也可能是右边)过期的从左边丢掉即可
然后我们用快速幂来处理要跳的次数(就是一次执行多次)
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#define R register//命令编译器将变量存放在寄存器中,而不是内存中,这样不用内存访址了
#define MAXN 1000010
typedef long long ll;
using namespace std;
ll n,k,m;
ll p[MAXN];
ll f[MAXN],ff[MAXN],ans[MAXN];//f数组存放每个点跳的下一个点
int main()
{scanf("%lld%lld%lld",&n,&k,&m);//n为青蛙数(也是点数)k是每次跳的距离,m是跳的次数for(R ll i=1;i<=n;i++) scanf("%lld",&p[i]);//输入每个点到起点的距离f[1]=k+1;//f[1]可以直接得出ll l=1,r=k+1;//滑动窗口模拟for(R ll i=2;i<=n;i++)//滑动窗口大小位k+1,存放每个点能跳的k+1个点(包括自身){ //(对上一个窗口处理)while(r+1<=n&&p[i]-p[l]>p[r+1]-p[i]) l++,r++;//窗口滑动若干格(如果新元素有更近的,那么最远的点必将淘汰,可能更新若干次哦)if(p[i]-p[l]>=p[r]-p[i]) f[i]=l;//之所以上个条件判断不取等,是因为取等时候我们会跳到下标更小的点else f[i]=r;//取值,要么是最左,要么是最右}for(R ll i=1;i<=n;i++) ans[i]=i;//初始跳0次while(m)//倍增(快速幂){if(m&1) for(R ll i=1;i<=n;i++) ans[i]=f[ans[i]];//遇到奇数,就更新答案一次,相当于少跳一次m>>=1;memcpy(ff,f,sizeof(ff));//将f赋给fffor(R ll i=1;i<=n;i++) f[i]=ff[ff[i]];//这是叠加跳的步数,依次为1,2,4,8,16,32(每次的步数)}//再进一步解释:我们要的是整体跳m次,相当于跳(m/2)次*2步; 相当于跳(m/4)次*4步; 相当于跳(m/8)次*8步for(R ll i=1;i<=n;i++) printf("%lld ",ans[i]);return 0;//撒由那拉
}小插曲:个人感觉快速幂是慢慢从走一步到走多步的,而倍增是从慢慢走多步到走一步的(逼近嘛)