第 3 章 Fourier级数的收敛性(Convergence of Fourier Series)
The sine and cosine series, by which one can represent
an arbitrary function in a given interval, enjoy
among other remarkable properties that of being convergent.
This property did not escape the great geometer (Fourier)
who began, through the introduction
of the representation of functions just mentioned,
a new career for the applications of analysis; it was
stated in the Memoir which contains his first research
on heat. But no one so far, to my knowledge, gave a
general proof of it…
(正弦和余弦,凭其可以表示任意已知区间上的函数,在其诸多属性中,除其它显著特性之外,还可享有其收敛性。这个属性并没有逃过伟大的几何学家(Fourier),他通过引入正弦和余弦的函数表示,开启了分析应用的新事业;这在回忆录中有所陈述,其中包括他对热的首次研究。但据我所知,到目前为止,还没有人给出它的通用证明……)
----------------------------------------------------------------------- G. Dirichlet [di:rikléi], 1829
在这一章中,我们继续我们的Fourier级数收敛性问题的研究。我们从两个不同的角度来处理这个问题。
第一个是从“全局的(global)”角度,关注整个闭区间[0,2π]上的函数 f 的所有行为。我们想到的结论是“均方收敛(mean-square convergence)”:假如函数 f 在圆周上可积,则当 时,有
。
这个结论的核心是“正交性(orthogonality)(译注:直角的,与垂直有关的)”的基本概念;这个概念基于两个量描述——具有内积的向量空间,以及与其相关的无限维变体Hilbert空间。一个关联结论是 Parseval[pázeifa:l]恒等式——其建立了函数的均方(mean-square)“范数(norm)”(译注:又称“范”或“模”)与其对应的Fourier系数范数之间的等式关系。正交性是一个基础的数学概念,它在分析学中有许多的应用。
第二个是从“局部有(local)”角度,关注的是函数 f 在某个已知的邻近点的行为。我们考虑的主要问题是逐点收敛问题:对于一个已知的 θ , f 的Fourier 级数收敛于 f (θ) 吗?我们首先证明,只要 f 在 θ 可微的时候,这个收敛性确实成立。作为一个推论,我们获得了Riemann[rí:ma:n]局部化原理,它表明, 是否完全收敛于 f (θ) 取决于在一个关于 θ 的任意小的区间上 f 的行为。这是一个著名的结论,因为函数 f 的Fourier系数(当然,还有Fourier级数)取决于 f 在整个闭区间[0,2π]上的取值。
1. Fourier级数的均方收敛(Mean-square convergence of Fourier series)
本节的目标就是证明下面的定理。
定理1.1 假如 f 在圆周上可积,则当 时,
。
正如我们前面所标识的那样,其涉及的关键概念是正交性。在一个向量空间中,正交性的正确设置是配置内积。
1.1. 向量空间和内积
向量空间的预备知识
一个实数域 ℝ (译注:R的双线写法)上的向量空间 V 是一个集合,其元素可以“被加”在一起,且可以按标量(scalars)“被乘”。更确切地说,我们可以将任意 X,Y ∈ V 的元素对,与集合V中一个称为它们和的元素关联起来,并将其和用 X + Y 表示。我们要求这个加法遵守通用的算术法则,例如,交换律 X + Y = Y + X ,以及结合律 X + (Y + Z ) = (X + Y ) + Z ,等等。此外,给定任意 X ∈ V 和实数λ ,我们赋予一个元素 λX ∈ V ,称其为 λ 与 X 的乘积。这种标量乘必须符合标准的属性,例如, 和
。我们可以允许用复数 ℂ (译注:C的双线写法)替换标量乘;则我们称 V 是复数域上的一个向量空间。
例如,实数 构成的d 元组(译注:d 个元素组成的元素组合)
是一个实数域上的向量空间。其加法按元组分量方式(componentwise)定义为
,
且与 λ∈ ℝ 的标量乘定义为:
。
类似地,空间 (前面例子的复数版本)是由复数
构成的d元组。它是一个复数域 ℂ 上定义的向量空间,其加法按元组分量方式定义为
。
且与 λ∈ ℂ 的标量乘定义为:
。
实数域 ℝ 上的向量空间V的内积(inner product)将空间V中的任意元素对 X , Y 与一个实数关联起来,我们将这个关联的实数表示为( X , Y )。特别地,内积必须是按双变量呈对称形式( X , Y ) = (Y ,X )和线性性;即,
(αX + βY ,Z ) = α( X ,Z) + β(Y,Z )
其中, α 与 β 是实数,且 X , Y ,Z ∈ V 。此外,我们要求内积为正定义(positive-definite),即,对于所有 V 中的 X ,( X , X ) ≥ 0 。特别地,已知一个内积(. , .),我们定义 X 的范数为
。
此外,如果 ||X || = 0 , 则意味着 X = 0 ,我们称内积为严格正定义。
例如,当 ,
时,空间
用严格正定义的内积定义为
。则
,
这就是常见的Euclid距离(Euclidean distance)。也可以使用记法|X |代替||X ||。
对于复数上的向量空间,两个元素的内积仍然是一个复数。此外,这样的内积称为Hermite[ermí:t]内积(非对称性)( 译注:Charles Hermite,法国数学家),因为它们必须满足 (译注:变换变量后内积的共轭)。因此,在下列两个变量中,第一个内积是线性的,第二个内积是共轭线性的:
和
。
此外,我们一定有 ( X , X ) ≥ 0 ,且定义 X 的范数为 ,这与前面一样。再有,假如 ||X || = 0 意味着 X = 0,则内积为严格正定义。
例如, 中的两个向量
和
的内积定义为
。
则,向量 Z 的范数形式由
给出。
向量空间上内积的出现允许人们定义“正交性”的几何概念。令 V 为向量空间(建立在实数域 ℝ 或复数域 ℂ ),其具有内积(. , .) 且与范数||.|| 关联。如果两个元素 X 和 Y 的内积 (X ,Y ) = 0 ,则元素 X 和 Y 是正交的,写成 X⊥Y。从正交性的概念出来,可以推出三个重要的结论:
() Pythagoras[paiθǽgəræs]定理(Pythagorean theorem):
假如 X 和 Y 是正交的,则 。
() Cauchy[kouʃ í]-Schwarz[swɔ:ts]不等式:
对于任意 X , Y ∈ V,我们有
|(X ,Y )| ≤ || X || || Y || 。
() 三角不等式:
对于任意 X , Y ∈ V,我们有
||X + Y || ≤ || X || + || Y || 。
证明这三个事实非常简单。
对于(i),展开(X + Y , X + Y )并应用假设条件 (X ,Y ) = 0 即可证明。
对于(ii),我们首先处理 || Y || = 0 这种情况,证明对所有所 X ,这意味着 (X ,Y ) = 0 。事实上,对于所有的实数 t ,我们有
以及 , 假如我们取 t 为一个很大的值并且可正(或负),则这与不等式矛盾。类似地,考虑
, 我们求得
。
假如 || Y || ≠ 0 ,我们可以设 ;则 X - c Y 与 Y 正交, 因此,也与 cY 正交,假如我们写成
并应用Pythagoras 定理,我们得到
。
对以上不等式两侧取平方根就得到预期的结果。注意,当 X = c Y 时,在上面式子中我们恰好取得等式。
最后,对于(iii),我们首先注意到
。
但 ,
, 且根据 Cauchy-Schwarz不等式有
。
两个重要的例子
向量空间 和
是有限维向量空间。在Fourier级数的背景下,我们必须处理两个无限维向量空间,我们现在对其进行描述。
复数域 ℂ上的向量空间 (译注:𝓁 是小写字母l的花体写法,ℤ 是Z的双线写法)是所有(双侧)无限复数序列
的集合,它使得
。
即,这个级数是收敛的。加法是按分量方式定义的,因此是标量乘。两个向量 和
按绝对收敛级数定义为
。
而 A 的范数形式由
给出。
首先,我们必须验证 是向量空间。这就要求,如果 A 和 B是
上的两个元素,则向量 A + B 也是其中的元素。为了理解这一点,对于每一个 N > 0 ,我们令
表示截断的元素, 其中,对于
任意|n|> N ,我们设
。我们以类似的方式定义截断元素
。则,根据在有限维Euclid[júklid]空间中成立的三角不等式,我们有
。
则
,
令 N 趋近无穷大,得到 。也可推断出,
,这就是三角不等式。Cauchy-Schwarz 不等式指出,
绝对收敛且
也可以按同样的方式从其有限类比推断出。
在这三个向量空间的例子 ,
和
中,它们的内积和范数符合两个重要属性:
() 内积严格正定义,即,
意味着
。
() 向量空间是完备的(completion),根据定义,指的是每一个 Cauchy序列按范数形式收敛于向量空间中的一个极限值。
具有以上两个属性的内积空间称为Hilbert[hílbət]空间。
我们现在给一个条件(i)和(ii)都不成立的准Hilbert空间的例子。
例子2。
令 ℛ (译注:ℛ 为字母R的修饰字体写法,LaTex语法为\mathcal(R),Word中的字体为Cambria Math,Unicode码为U+0211B(ALT+X快捷键转换))表示闭区间[0,2π]上(或等价地,圆周上的可积函数)复值Riemann可积函数族。这是一个复数域 ℂ 上的向量空间,加法逐点定义为
。
自然地,与标量λ∈ℂ 的乘法定义为
。
向量空间上的内积定义为
(1) 。
则 f 的范数定义为
。
读者需要验证类似 Cauchy-Schwarz 和三角不等式的属性在此示例中是否成立;即, 和
。虽然这些事实可以作为前面示例中相应不等式的结果而获得,但论证有点复杂,我们更愿意以不同的方式进行。
首先,我们观察到,对于任意两个实数A 和 B,有 , 假如我们令
和
且有 λ > 0 ,我们得到
。
则当我们对这个不等式按θ 积分时得到
。
则,代入 便得到Cauchy-Schwarz不等式。则,正如我们前面所见一样,三角不等式只是一个简单的结果。当然,我们选取λ时我们必须假设 || f || ≠ 0 且 || g || ≠ 0 ,这又会把我们引入下面的观察。
在 ℛ 中,条件(i)对于Hilbert空间不成立,因此|| f || = 0 仅意味着 f 在其连续点消失。这不是一个很严重的问题,因为在附录中,我们证明可积函数是连续的(除了“微不足道(negligible)”的集合之外),因此|| f || = 0 就意味着 f 除了在某些“0测度”集合之外是消失的。实际上,人们可以通过采用0函数这样的约定来绕过 f 不等于0有困难,因为为了积分的目的,f 表现得正好像0函数。
更本质的困难在于ℛ 是不完备的。理解这一点的一种方式是从函数
出发。因为是 f 无界的,所以,它不属于空间 ℛ 。由截断序列 定义的序列
可以很容易地看成构成空间ℛ 中的一个Cauchy序列(见练习5)。然而,这个序列不收敛于空间ℛ 中的一个元素,因为极限一定会是 f (如果存在的话);另一个例子,见练习7。
这个以及更复杂的例子激发了对 ℛ的完备性的探索,这类函数是闭区间[0,2π]上Riemann可积函数。这种完备性的构造和识别——Lebesgue函数类 ( [0,2π] ) ,代表着分析学上的一个重要转折点(有点类似于前面提到的比率函数的完备性,即,从 ℚ 到 ℝ 的通道 )。这些基础概念的详细讨论将推后到第III册书,届时我们将以Lebesgue积分理论开始。
现在,我们转向定理1.1的证明。
1.2. 均方收敛的证明(Proof of mean-square convergence)
考虑圆周上具有内积
的可积函数空间 ℛ 以及由
定义的范式。要使用这种记法,我们必需证明当 时,
。对于每一个整数 n,令
, 并注意到族
是规范正交的(orthonormal);即,
。
令 f 为单位圆周上的可积函数,并令 表示Fourier系数。一个重要的观察是,这些Fourier系数是通过 f 与正交集
中的元素构成的内积表示的:
。
特别地, 。则族
的规范正交属性与
这个事实意味着对于所有
,
之差与
是正交的。因此,对于任意复数
,我们一定有
(2) 。
从这个事实,我们总结出两个结论。
第一,我们可以应用Pythagoras定理于下列分解式
,
其中,我们现在选择 (译注:即以上式子(2)中的任序
),我们得到
因为族 具有规范正交性意味着
,
我们推断出
(3) 。
第二,从(2)中我们可以总结出下面的简单引理。
引理1.2 (最优逼近)(Best approximation) 假如f 是圆周上具有Fourier系数 的可积函数,则对于任间复数
,有
,
此外,对于所有的 , 仅当
时,等号成立。
证明:
应用 Pythagoras 定理可立即推出下列等式
,
其中, 。
这个引理有一个清晰的几何解释。它指的是在范式||.||中最接近 f 的至多N次三角多项式是部分和 。这个部分和的几何属性如图1所描述,其中 f 在序列
所跨越的平面上的正交投影正好是
。

----------------------------------------------------------图1 最优逼近引理----------------------------------------------
使用最优逼近引理,我们现在可以给出 的证明,以及证明重要事实——三角多项式在圆周上的连续函数空间中是稠密的(dense)。
假如 f 在圆周上是连续的。则,给定 ε > 0 , 存在(根据第二章推论5.4)一个三角多项式 P,假如其次数为 M ,使得,对于所有的θ,有
。
特别地,取平方并对这个不等式积分就产生 ,应用最优逼近引理我们推断出,只要 N ≥ M , 就有
。
当 f 是连续的时候,这就证明了定理1.1。
假如f 仅可积,我们不能用三角多项式一致地逼近 f 。反之,我们应用第二章中的逼近引理3.2 并选择一个圆周上的连续函数 g 并满足
以及
。
则,我们得到
。
现在,我们可以使用三角多项式 P 逼近函数 g,使得 。则
,且我们可以再一次应用最优逼近引理推断。这就完成了证明命题—— f 的Fourier级数的部分和按均方范式||.|| 收敛于 f 。
注意,这个结论以及关系式(3)意味着,假如 是可积函数 f 的第 n 项Fourier系数,则级数
收敛,且,事实上,我们有 Parseval[pá:zeifa:l] 恒等式
。
这个恒等式建立了两个向量空间 和 ℛ 中范式之间的重要联系。
我们现在总结一下一节的结论。
定理1.3 令 f 为圆周上具有 的可积函数,则我们有:
() Fourier级数均方收敛,即,当
时,
。
() Parseval恒等式,即
。
评注1 :
假如 是圆周上函数的任意规范正交族,且
, 则从关系(3) 我们可以推断出
。
这称为Bessel[bésəl]不等式。仅当族 恰好也是一个“基(basis)”的时候等号成立(与Parseval不等式一样),即,在此意义上——当
时,
。
评注2 :
我们可以将每一个可积函数与其Fourier系数构成的序列 关联起来。Parseval恒等式确保了
。 因为
是Hilbert空间,前面讨论的 ℛ 不具完备性可以这样理解:存在一个序列
,使得
,然而,不存在这样的Riemann可积函数F——对于所有的n , 其第 n 项Fourier系数等于
。习题6中给出了这样的例子。
由于收敛级数的项趋近于0,我们从Parseval恒等式或Bessel不等式推断出随后的结论。
定理1.4 (Riemann-Lebesgue引理) 假如 f 是圆周上的可积函数,则当 时,
。
这个命题的一个等价重述是,假如 f 在 [0,2π ]上可积,则,当 时,
且
。
为了对本节做总结,我们给出Parseval恒等式的更多通用版本,这些恒等式我们在下一章将会用到。
引理1.5 假如 F 和 G为圆周上的可积函数,且其分别有Fourier级数
和
。
则
。
回顾在例子1中的讨论可知,级数 绝对收敛。
证明:
证明可从Parseval恒等式以及事实
推断出,以上两者在每一个 Hermite内积空间中都成立。这个事实的验证留给读者去完成。
2. 回到逐点收敛
均方收敛定理并不能更进一步地深入洞悉逐点收敛问题。事实上,定理1.1并不能确保对于任意θ Fourier级数都收敛。练习3有助于解释这种现象。然而,假如一个函数在某一点 可微,则其Fourier级数在
点处收敛。在证明了这个结论之后,我们给出一个在某一点具有发散Fourier级数的连续函数的例子。这些现象表明了Fourier级数理论中逐点收敛问题的复杂性(intricate)。
2.1. 一个关于局部化结论
定理 2.1 令 f 为圆周上的可积函数,且在 点处可微。则当 N 趋近于无穷大时,
。
证明:
定义
。
首先,F 在0 附近有界,因为其在 0 附近可微。其次,对于任意小的 δ ,函数 F 在区间上是可积的,因为 F 可积并且 |t | > δ 。根据附录中命题1.4的结论,函数 F 在整个闭区间 [-π,π]上是可积的。我们知道,
, 其中
是 Dirichlet核。因为
, 我们求得
。
我们回顾
,
其中,系数(quotient)函数在闭区间[-π,π]上是连续的。因为我们可以写成
,
我们应用 Riemann-Lebesgue 引理到Riemann可积函数 和
以完成定理的证明。
注意到,假如我们仅假设 f 在 点满足一个 Lipschitz[lípʃits]条件(译注:Lipschitz是德国数学家),则定理所述的结论仍然成立;即,
对于某些 M ≥ 0 和所有 θ 成立。这种说法与称 f 满足一个阶次 α = 1 Hölder[hə:ldə]条件等价。
这个定理的一个显著结果是Riemann局部化原理(the localization principle of Riemann)。这个结论指出, 的收敛性仅取决于 f 在
附近的行为。最初,这并不明确,因为构成Fourier级数要求对 f 在整个圆周上积分。
定理2.2 假设 和
是定义在圆周上的两个可积函数,且对于某个
, 存在一个包括
的开区间
, 使得对于所有
,有
。
则当 趋近于无穷大时,
。
证明:
在 中,
是0 ,因此它在
点是可微的,且我们可以应用前面的定理来推断这个证明。
2.2. 一个具有发散Fourier级数的连续函数
现在我们将注意力转向一个连续周期函数的例子,它的Fourier级数在某一点发散。 因此,如果可微性的假设被弱化的连续性的假设所取代(译注:可微性更严格,可微一定连续,但连续不一定可微),则定理 2.1 将不成立。我们的反例(counter-example)表明,这个看似合理的(plausible)假设(hypothesis)(译注:指函数在积分区间上连续的这个弱化的假设)实际上是错误的;此外,它的构建也阐明了该理论的一个重要原则。
这里涉及的原理称为“打破对称(symmetry-breaking)”(注:我们从物理学借用这个术语,在物理中它用在一个完全不同的背景下)。我们想到的对称是出现在函数的Fourier展开式中的频率 和
之间的对称。例如,部分和算子(partial sum operator)以反映这种对称的方式定义。此外,Dirichlet核,Fejèr核 和 Poisson核都是这种意义上的对称性。打我们打破这种对称性时,即,当我们将Fourier级数
拆分成
和
两个部分时,我们就引入新的且影响深远的现象。
我们给一个简单的例子。我们以齿状函数 f 开始,其按 θ 为自变量为奇函数,且当 时,
。则,根据第2章练习8 ,我们知道
(4) 。
现在,我们考虑打破对称性的结果,打破对称导致的级数为
。
则,不同于(4) , 以上的级数不再是Riemann可积函数的Fourier级数。事实上,假如它是Riemann可积函数的Fourier级数,比如为 ,特别地,其中的
有界。使用Abel均值,则,我们有
,
当 r 趋近于1 时,其趋近于无穷大,因为此时 发散。这就得出了预期的矛盾。因为
,
其中, 表示前面章节讨论的Poisson核。
齿状波函数是我们用来塑造(fashion)反例的对象。我们按随后的方式进行。对于每一个 N ≥ 1, 我们在闭区间 [-π,π]上定义如下两个函数,
和
。
我们主张(contend)两点:
()
。
()
按 N 和 θ 一致有界。
第一种表述是事实 的结果 ,这很容易建立(另见图2):
。
为了证明(ii), 我们按照与证明Tauber[táubə]定理一样的思路去论证,这种思想指的是,假如级数 是Abel可积于 s 且
,则实际上
收敛于s (见第2章练习14)。实际上,Tauber定理的证明非常类似下面的引理。
引理2.3 假如级数 当
趋近于 1 (
) 时是有界的。
假如 , 则部分和
是有界的。
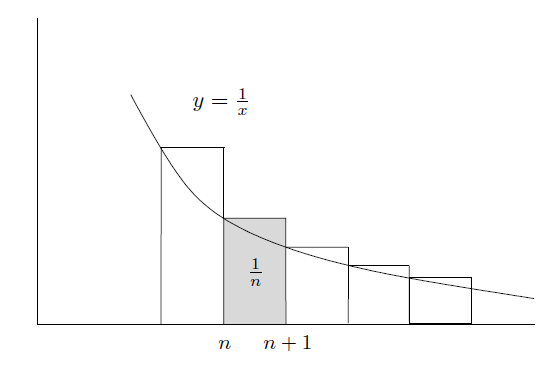
---------------------------------------------------图2 比较总和与积分--------------------------------------
证明:
令 , 且选择
使得
。我们估算差值
为如下:
,
其中,我们已经用到了简单的观察结果
。
因此,我们看到,假如 同时满足
且
两个条件,则
。
我们应用这个引理到级数 ,这是上面用到的齿状函数的 Fourier 级数。这里,对于
,
, 因此,显然
。最后,这个级数的Abel均值是
。但 f 是有界的且
是好核。因此,
按 N 和 θ 一致有界,正如所证明的那样。
现在我们来到问题的核心。注意到, 和
都是 N 次的三角多项式(即,仅当
时,它们有非零Fourier系数)。现在,我们据此通过用个2N 个单位分别替换掉
和
的频率,便构成了次数分别为
和
的三角多项式
和
。换句话说,我们定义
和
。因此,当
时,
具有非消减的Fourier系数,而现在,对
且
,
的系数是非消减的。此外,
是
的对称中心,而现在
是
的对称中心。下面我们考虑部分和
。
引理2.4
。
从上面所述和图3很容易明了。

--------------------------------------------------引理2.4中的打破对称性------------------------------------------
这个影响在于,当 时,算子
打破了
的对称性,但是在引理覆盖的其它情况下,
的行为相对“温和(benign)”, 因为在那些情况,输出结果要么是
要么是0。
其次,我们必须求得正项序列 的收敛级数和递增得足够快的整数序列
以使得:
()
,
(
) 当
时
。
我们选取(例如) 和
,很容易看出其满足以上的标准。
最后,我们可以写下我们期望的函数。即,
。
由于 一致有界(回顾
),上面这个级数一致收敛于某个连续周期函数。然而,根据我们上面的引理我们得到,当
时,
。

---------------------------------------中间区间 中打破对称性------------------------------
事实上,对应于 (
或
) 的项分别贡献了
或 0 (因为序列
一致有界),而对应于
的项以绝对值形式大于
, 因此
。因此,
在 0 处的Fourier级数的部分和是无界的,我们完成了证明,因为这证明了
在
处的 Fourier级数的发散性。为了产生一个其级数在任意其它预先分配的
处发散的函数,只需考虑函数
足可。
内容来源:
<<Fourier Analysis: An Introduction>> E.M. Stein & R. Shakarchi