Day42 力扣动态规划 :123.买卖股票的最佳时机III |188.买卖股票的最佳时机IV
- 123.买卖股票的最佳时机III
- 第一印象
- 看完题解的思路
- dp数组:
- 递推公式:
- 初始化
- 遍历顺序
- 实现中的困难
- 感悟
- 代码
- 188.买卖股票的最佳时机IV
- 第一印象
- 初始化
- 递推公式
- 看完题解的思路
- 实现中的困难
- 感悟
- 代码
123.买卖股票的最佳时机III
这道题一下子就难度上来了,关键在于至多买卖两次,这意味着可以买卖一次,可以买卖两次,也可以不买卖。
视频讲解:https://www.bilibili.com/video/BV1WG411K7AR
https://programmercarl.com/0123.%E4%B9%B0%E5%8D%96%E8%82%A1%E7%A5%A8%E7%9A%84%E6%9C%80%E4%BD%B3%E6%97%B6%E6%9C%BAIII.html
第一印象
这道题变成最多买卖两次:买卖0,1,2次都合理。
感觉挺难的,直接看题解吧。
看完题解的思路
分析一下题目里的状态,因为最多买入两次,所以有第一次的持有+不持有、第二次的持有+不持有。

但其实不操作这一种情况可以不管。
dp数组:
如上图所示
第 i 天在 0~4状态时,剩的最大金额是dp[i][0] ~ dp[i][4]
递推公式:
对于dp[i][1] ,第一次有股票
- 延续前一天的第一次有股票状态:dp[i-1][1]
- 这一天进行了买入才有股票: -price[i]
对于dp[i][2] ,第一次没有股票
- 延续前一天的第一次没有股票的状态:dp[i-1][2]
- 这一天进行了卖出才没有股票: dp[i-1][1] + price[i]
对于dp[i][3],第二次有股票
- 延续前一天第二次有股票状态: dp[i-1][3]
- 这一天进行了买入,才有股票:dp[i-1][2] - price[i]
对于dp[i][4],第二次没有股票
- 延续了前一天第二次没有股票的状态:dp[i-1][4]
- 这一天进行了卖出才没有股票:dp[i-1][3] + price[i]
每一次都选择更大的状态
初始化
dp[0][0] = 0
dp[0][1] = -price[I]
dp[0][2] = 0
dp[0][3] = -price[I]
dp[0][4] = 0
看做第一天买入卖出,又买入卖出
遍历顺序
正序遍历就行
实现中的困难
代码上不难
感悟
这道题我觉得难于思考的有两个地方:
- 五种状态如何转移,在看完题解的思路那说得很清楚了
- 如何理解初始化:第一次买卖好理解,但是第二次再买卖不怎么好理解
第二种的问题也直接导致了,这道题其实可以只买一次。**那么最后如何理解,只需要直接return dp[length][4] 。**因为它包含了买两次的,也包含了只买一次的情况。
我们手写一个只买一次的情况
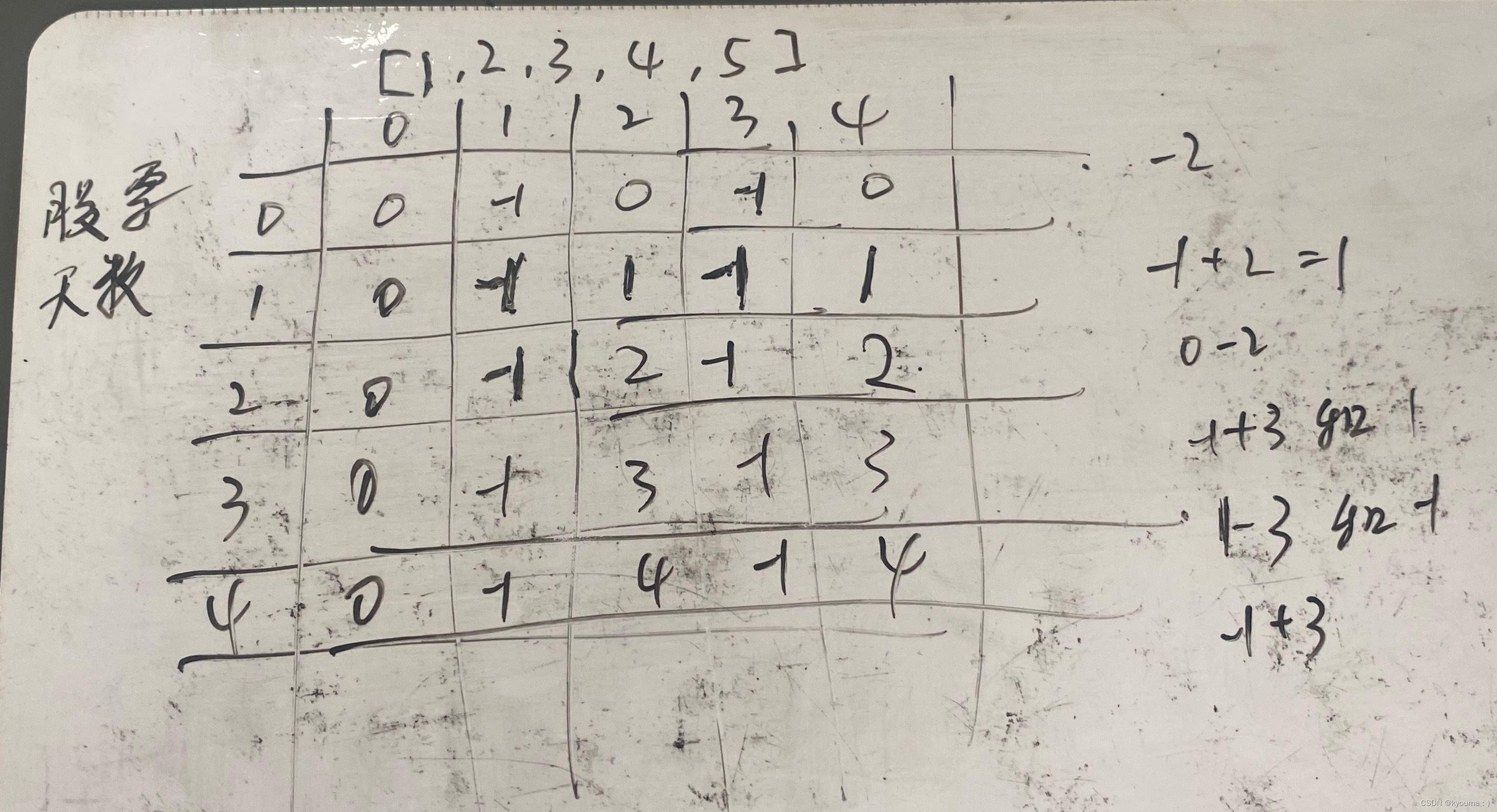
我们会发现,每一天第一次卖出的情况是在不断更新的,第二次卖出和第一次卖出的数值也是一样的。
我觉得可能是因为初始化的时候,第二次买卖的状态就是当天买当天卖。之后这个状态一直持续在表格里。
比如2-2的位置代表,第一天买第三天卖出有最多收益,2-4的含义也是第一天买第三天卖出有最多的收益。
我认为, 它们是重复的,所以可以看作2-4 就是 2-2的当天再次买卖的情况,但本质上他们是重复的。
这里画出一个两次买卖的图就更能清晰的对比了,明白第二次买卖是怎么变的和第一次不一样的,但我懒了。
上课去咯
代码
class Solution {public int maxProfit(int[] prices) {int[][] dp = new int[prices.length][5];dp[0][0] = 0;dp[0][1] = - prices[0];dp[0][2] = 0;dp[0][3] = - prices[0];dp[0][4] = 0;for (int i = 1; i < prices.length; i++) {dp[i][0] = dp[i - 1][0];dp[i][1] = Math.max(dp[i - 1][1], - prices[i]);dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);}for (int i = 0; i < dp.length; i++) {for (int j = 0; j < 5; j++) {System.out.print(dp[i][j] + " ");}System.out.println();}return dp[prices.length - 1][4];}
}
188.买卖股票的最佳时机IV
本题是123.买卖股票的最佳时机III 的进阶版
视频讲解:https://www.bilibili.com/video/BV16M411U7XJ
https://programmercarl.com/0188.%E4%B9%B0%E5%8D%96%E8%82%A1%E7%A5%A8%E7%9A%84%E6%9C%80%E4%BD%B3%E6%97%B6%E6%9C%BAIV.html
第一印象
我觉得我行
上一道题是最多 2 次买卖,就对应 第一次有、没有 + 第二次有、没有四种状态。
那么k次买卖,就对应第一次有、没有……第k次有、没有
也就是数组大小从 4 变成 2*k
然后按之前的套路去取最大值就行了。
初始化
初始化的时候有点小麻烦,因为每一次有两种状态,所以 for 循环要以 两种状态 为一次去做。就是 j += 2 而不是 j++
递推公式
递推公式也是,for 循环要以 两种状态 为一次去做。就是 j += 2 而不是 j++
这个地方需要注意!!!
对于 j = 0 的情况,如果在 i 天,计算第一次拥有的最大钱。应该是比较 i - 1天就第一次拥有的金额 和 在这一天进行第一买入的 -price[i]
因为第一次买入,不需要依赖上一天卖出的价格。
如果是计算 i 天,第三次拥有的最大钱。就是比较 i -1天就第三次拥有的金额 和 在这一天进行第三次买入的 dp[i-1][3] - price[i]
看完题解的思路
和我写的类似,他保留了 不操作 的那个状态。
实现中的困难
没有处理 j = 0的情况,就是在递推公式那里我提到的。
感悟
感觉股票问题很套路
代码
class Solution {public int maxProfit(int k, int[] prices) {//dp数组int[][] dp = new int[prices.length][2 * k];//初始化for (int j = 0; j < 2 * k; j += 2) {dp[0][j] = -prices[0];dp[0][j + 1] = 0;}//状态转移 //对于每一天来说for (int i = 1; i < prices.length; i++) {//第 j 次有股票和第j次没股票for (int j = 0; j < 2 * k; j += 2) {//第一次if (j == 0) {//昨天就有了,今天是第一次有,所以是-price[i]dp[i][j] = Math.max(dp[i - 1][j], - prices[i]);//昨天就没有、今天才没有dp[i][j + 1] = Math.max(dp[i - 1][j + 1], dp[i - 1][j] + prices[i]);} else {//昨天就有了、今天才有dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - 1] - prices[i]);//昨天就没有、今天才没有dp[i][j + 1] = Math.max(dp[i - 1][j + 1], dp[i - 1][j] + prices[i]);}}}return dp[prices.length - 1][2 * k - 1];}
}
![[Machine Learning][Part 8]神经网络的学习训练过程](https://img-blog.csdnimg.cn/ad872654c35e4ac6954852d5d8a590f3.png)