- 300.最长递增子序列
- 674. 最长连续递增序列
- 718. 最长重复子数组
第一题:最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
- 输入:nums = [10,9,2,5,3,7,101,18]
- 输出:4
- 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
动态规划的方法解决:
(1)确定dp数组以及下标的含义
dp[i]:表示i 之前包括i 的以nums[i] 结尾的最长递增子序列的长度
(2)状态转移方程
位置i 的最长升序子序列等于j 从0到i-1各个位置的最长升序子序列+1的最大值
所以:if(nums[i] > nums[j]) dp[i]=max(dp[i],dp[j]+1);
(3)dp[i]的初始化
每一个i,对应的dp[i] (即最长递增子序列)起始大小至少都是1
(4)确定遍历顺序
dp[i]是由0到i-1各个位置的最长递增子序列推导而来,所以遍历i一定是从前向后遍历
j其实就是遍历0---i-1,那么是从前向后,
(5)举例推导
输入:[0,1,0,3,2],dp数组变化如下:
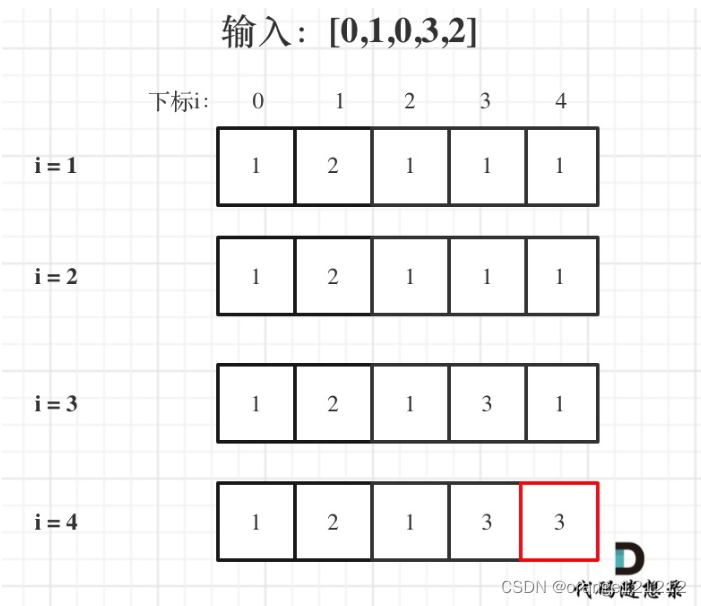
第二题:最长连续递增序列
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1:
- 输入:nums = [1,3,5,4,7]
- 输出:3
- 解释:最长连续递增序列是 [1,3,5], 长度为3。尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
本题相较于上一题,有一个限制在于连续递增,就是说子序列的元素在原序列中是连续的。反而简单了,如果出现nums[i]>nums[i-1],计数再重头开始
动态规划五部曲:
(1)确定dp数组以及下标的含义
dp[i]:以下标i为结尾的连续递增的子序列长度为dp[i]。
(2)确定递推公式
如果nums[i] > nums[i-1] ,那么以i为结尾的连续递增的子序列长度一定等于i-1结尾的连续递增子序列的长度+1;其实也是站在结果往前看,dp[i]的结果取决于dp[i-1]
(3)dp数组如何初始化
子序列长度最少也应该是1,所以dp[i]初始化为1;
(4)确定遍历顺序
dp[i+1]依赖dp[i],所以一定是从前向后遍历
(5)举例推导数组
nums=[1,3,5,4,7],跟前一个元素作比较

第三题:最长重复子数组
给两个整数数组 A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。
示例:
输入:
- A: [1,2,3,2,1]
- B: [3,2,1,4,7]
- 输出:3
- 解释:长度最长的公共子数组是 [3, 2, 1] 。
0、首先子数组是连续子序列,要求两个数组中最长重复子数组,第一层含义是两个数组求出最长的连续子数组,第二层含义是,重复的子数组(最长的)的长度是多少。
1、动态规划五部曲
(1)确定dp数组以及下标的含义
dp[i][j]:以下标i-1为结尾的A,和以下标j-1为结尾的B,最长重复子数组长度为dp[i][j]。
此时dp[0][0]的含义是什么?
(2)确定递推公式
根据dp[i][j]的定义,dp[i][j]只能由dp[i-1][j-1]推导出来。
即当A[i-1]和B[j-1]相等的时候,dp[i][j]=dp[i-1][j-1]+1
(3)dp数组如何初始化
根据dp[i][j]的定义,dp[i][0]和dp[0][j]没有意义,方便递归,所以初始化为0
(4)确定遍历顺序
不管是外层遍历A,内层遍历B,或者是反过来都可以
遍历的时候记录dp[i][j]的最大值
(5)举例推导
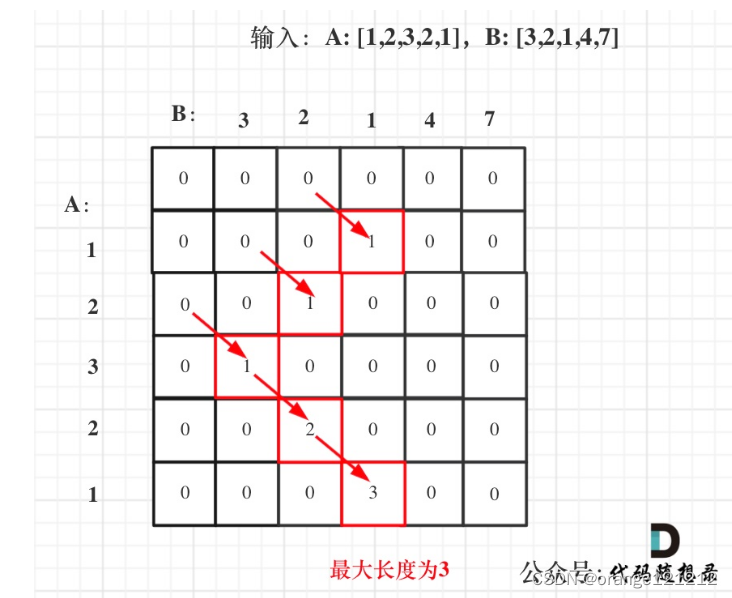
总结:前两个理解比较简单,第三题略难,关于dp[i][j]和dp[i-1][j-1]的关系



![[PHP]Tpflow工作流引擎 v6.0.9](https://img-blog.csdnimg.cn/d1532a07797e47649f00df81d830513f.png)