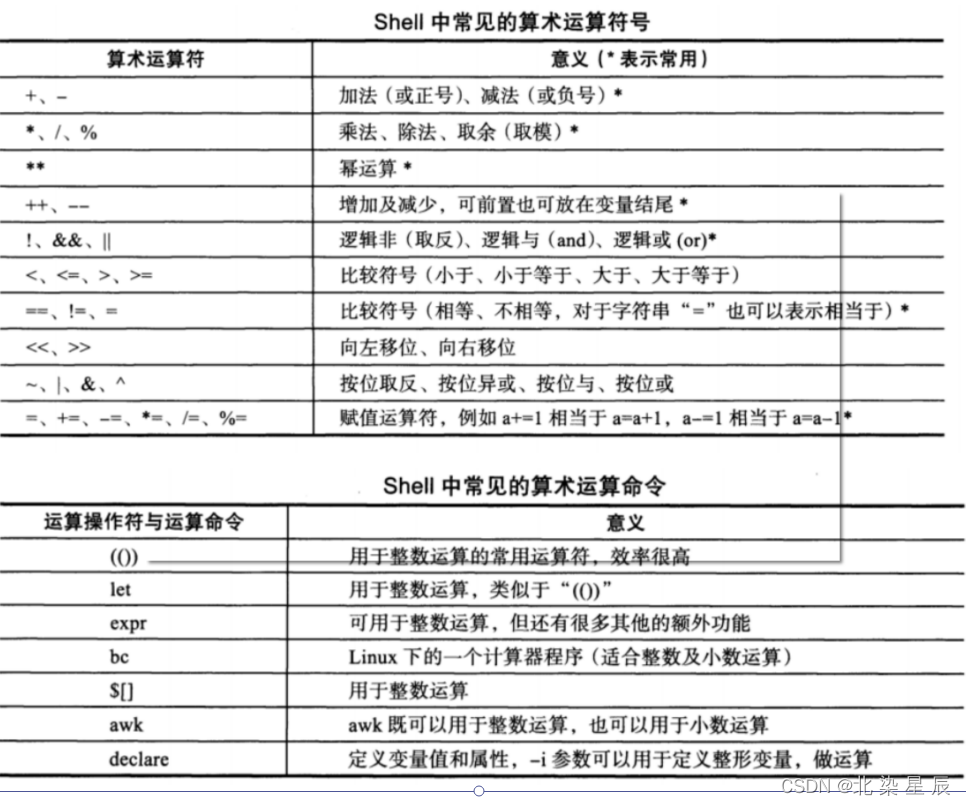
这个是反相比例运算放大电路,输出电压等于-Rf/R1乘以输入电压。
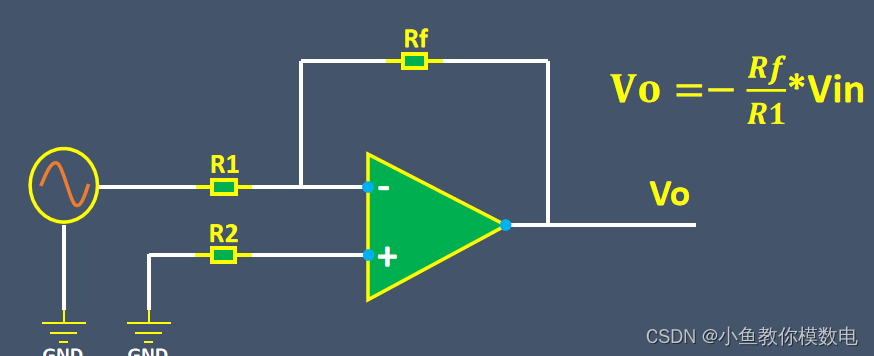
这个是同相比例运算放大电路,输出电压等于1+Rf/R1乘以输入电压。
大家可以看到这两个电路中,都有一个电阻R2,反相比例运算放大电路放在同相端到地,同相比例运算放大电路放在输入信号和同相端之间。
电阻R2我们一般叫做平衡电阻或者补偿电阻。它的阻值等于 R1和Rf并联的值。

对于理想运放而言,输入电阻为无穷大,我们认为没有电流流入运放的输入端。
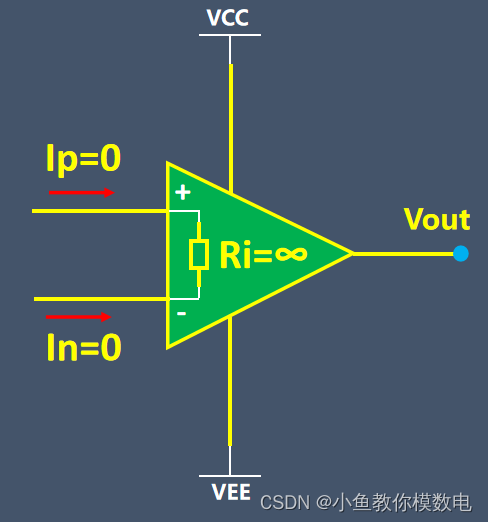
但是实际上运放的输入部分一般为三极管或场效应管,对于三极管输入的运放来说,三极管工作在放大区是需要一定的偏置电流的,对于运放来说这个电流一般是nA级别。
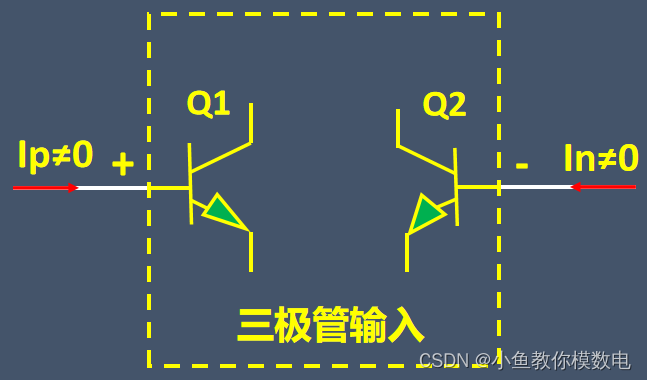
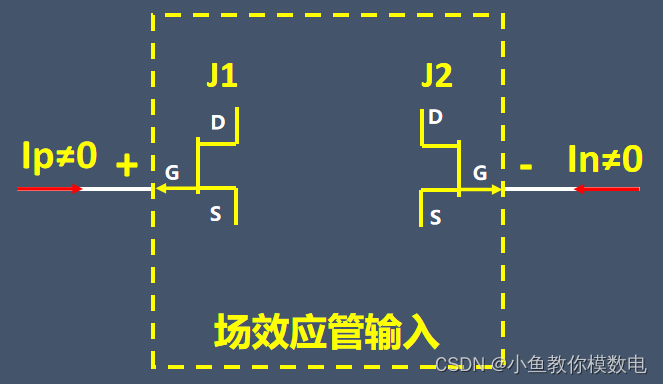
对于场效应管输入的运放来说,会存在一定的漏电流,一般是pA级别。
运放的输入偏置电流等于
对于反相比例运算放大电路,如果我们单独计算Ip和In对输出电压的影响,这时我们将输入信号短路。
可以得到Ip和In产生的输出电压。
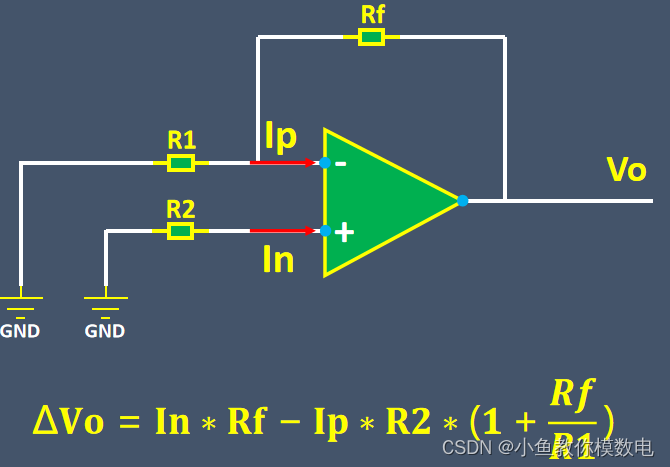
一般我们认为运放同相端和反相端的偏置电流是相等的,我们记作 那么上面的公式就简化成这一个。

当R2=R1//Rf时,输出电压为0,这时运放输入偏置电流导致的输出电压为零,所以比例运算放大电路平衡电阻的作用就是消除输入偏置电流对输出电压的影响。
但是一般运放同相端和反相端偏置电流由于输入级器件不可能做到完全相同,所以他们是存在差异的,这两个值的差我们称之为运放的输入失调电流,用Ios表示,Ios一般比IB要小一些
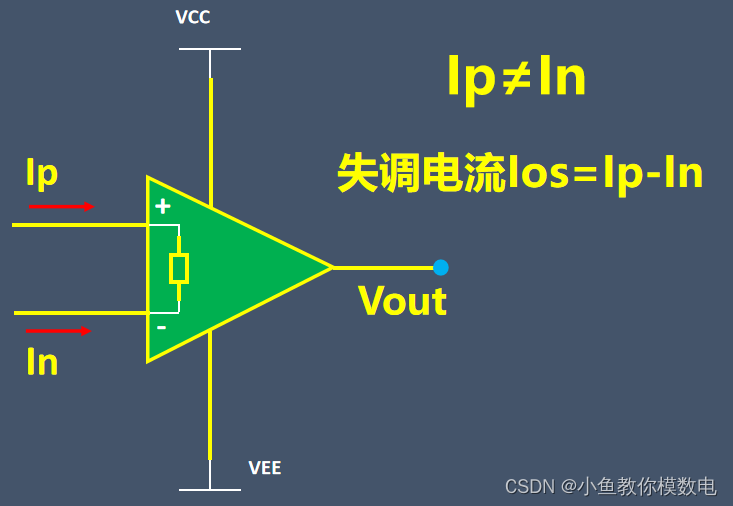
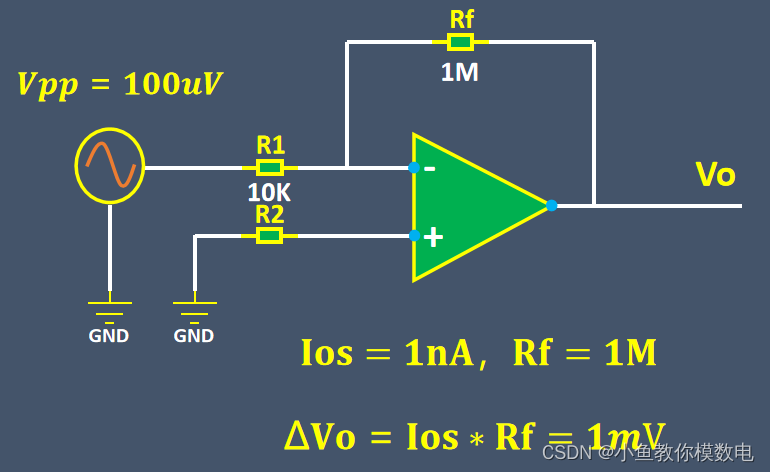
所以即使引入了平衡电阻,偏置电流还是会产生一定的输出电压。
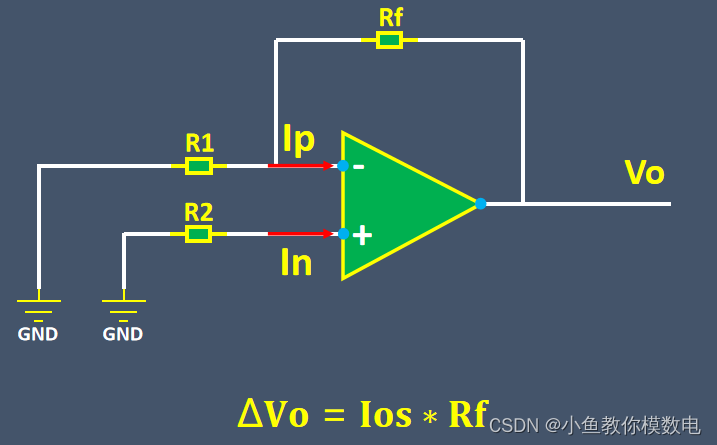
由于Ios非常小,一般是nA级别,所以输入偏置电流产生的输出电压也很小, 通常情况下,这样的误差是可以忽略的。
但是对于要放大很微弱信号的场合,比如信号本身是uV级别,此时输入偏置电流产生的误差可能就不能忽略了,因此需要选用输入偏置电流和失调电压更小的精密运放。