1.什么是线性表

线性表（linear list）是n个具有相同特性的数据元素的有限序列。线性表是一种在实际中广泛使用的数据结构，常见的线性表：顺序表、链表、栈、队列、字符串...

线性表在逻辑上是线性结构，也就说是连续的一条直线。但是在物理结构上并不一定是连续的，线性表在物理上存储时，通常以数组和链式结构的形式存储。

2.什么是顺序表

顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构，一般情况下采用数组存储。在数组上完成数据的增删查改。

顺序表一般可以分为：

1.静态顺序表：使用定长数组存储元素。

2.动态顺序表：使用动态开辟的数组存储元素。

3.静态顺序表结构的定义

#define N 100
typedef int SLDataType;//静态顺序表
typedef struct SeqList
{SLDataType a[N];//定长数组int size;//记录存储多少个有效数据
}SeqList;

4.静态顺序表的函数接口实现

//初始化顺序表
void SLInit(SeqList* ps);
//静态顺序表的尾插
void SLPushBack(SeqList* ps,SLDataType data);
//静态顺序表的尾删
void SLPopBack(SeqList* ps);
//静态顺序表的头插
void SLPushFront(SeqList* ps,SLDataType data);
//静态顺序表的头删
void SLPopFront(SeqList* ps);
//pos位置插入数据
void SLInsert(SeqList* ps, int pos, SLDataType data);
//pos位置插入数据
void SLErase(SeqList* ps,int pos);
//查找数据
int SLFind(SeqList* ps, SLDataType data, int begin);
//判断数组是否已满
bool IsFull(SeqList* ps);
//打印存储的数据
void SLPrint(SeqList* ps);

以下是函数接口的实现：

void SLInit(SeqList* ps)
{assert(ps);ps->size = 0;
}

bool IsFull(SeqList* ps)
{assert(ps);if (ps->size == N){return true;}else{return false;}
}

void SLPushBack(SeqList* ps,SLDataType data)
{assert(ps);assert(!IsFull(ps));//插入数据ps->a[ps->size] = data;ps->size++;
}

void SLPopBack(SeqList* ps)
{assert(ps);ps->size--;
}

void SLPushFront(SeqList* ps, SLDataType data)
{assert(ps);assert(!IsFull(ps));//挪动数据for (int i = ps->size - 1; i >= 0; i--){ps->a[i + 1] = ps->a[i];}//插入数据ps->a[0] = data;ps->size++;
}

void SLPopFront(SeqList* ps)
{assert(ps);assert(ps->size > 0);//挪动数据for (int i = 0; i < ps->size-1; i++){ps->a[i] = ps->a[i + 1];}ps->size--;
}

void SLInsert(SeqList* ps, int pos, SLDataType data)
{assert(ps);assert(!IsFull(ps));//挪动数据for (int i = ps->size-1; i >= pos; i--){ps->a[i + 1] = ps->a[i];}//插入数据ps->a[pos] = data;ps->size++;
}

void SLErase(SeqList* ps, int pos)
{assert(ps);assert(ps->size > 0);//挪动数据for (int i = pos; i < ps->size - 1; i++){ps->a[i] = ps->a[i + 1];}ps->size--;
}

int SLFind(SeqList* ps, SLDataType data, int begin)
{assert(ps);assert(begin < ps->size);for (int i = begin; i < ps->size; i++){if (ps->a[i] == data){return i;}}return -1;
}

void SLPrint(SeqList* ps)
{assert(ps);for (int i = 0; i < ps->size; i++){printf("%d ", ps->a[i]);}printf("\n");
}

5.静态顺序表的问题及思考

1.静态顺序表的局限性

静态顺序表只适用于确定知道需要存多少数据的场景。如果数据量未知，N的值太大，造成空间浪费；N的值太小，数据存储不下。

2.接口函数的参数为什么要用结构体指针？

因为尾插、尾删与初始化需要改变结构的内容，若不用结构体指针，形参的改变无法影响实参，则导致无法完成任务；剩下的两个是为了统一与美观。

3.顺序表增删查改的时间复杂度

①顺序表的优势

顺序表的优势是尾插与尾删，为什么呢？

顺序表底层逻辑结构与数组相同，都是在内存上取一连串连续的空间来存储数据。既然这些空间是连续的，那么就意味着我们只需要记住这一连串空间的起始位置，若需要访问与起始位置只相差距离为5的位置时，我们只要在起始位置的地址上加5就可以一步到位。

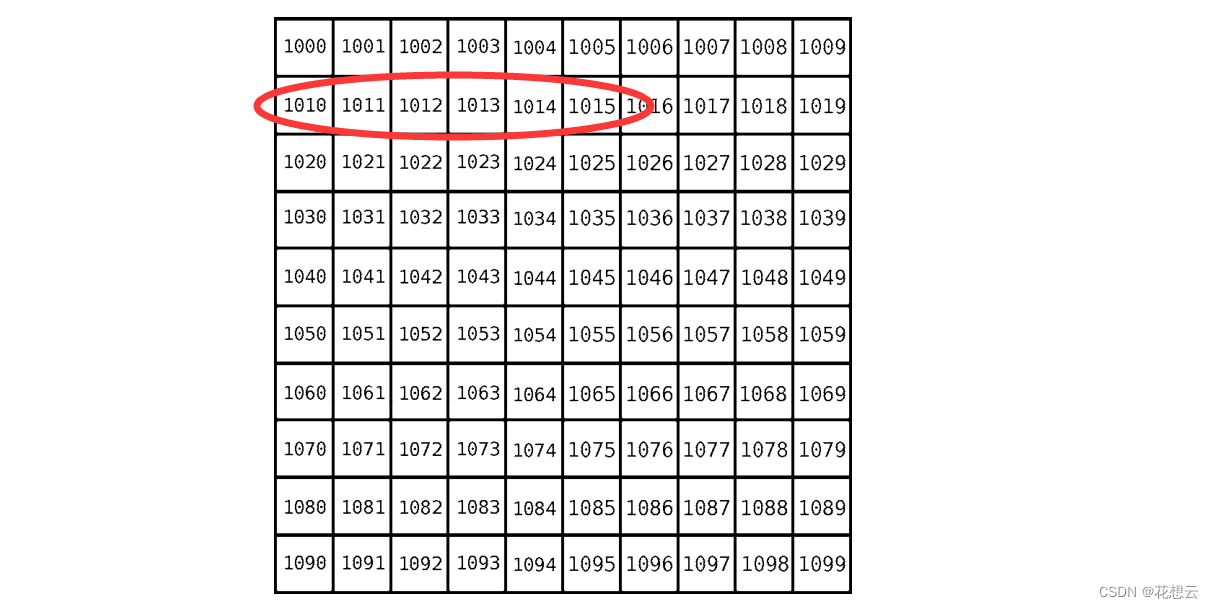尾插与尾删最重要的一步就是如何找到尾巴。然而数组几乎可以一步做到这一点，我们知道数组的起始位置，而且用size记录着数组有效长度，那么找尾可以说是及其简单，一步到位。

所以顺序表的尾插与尾删时间复杂度为O(1)。

②顺序表的劣势

与尾插尾删相比，顺序表最大的劣势就是头插与头删。

数组的空间开辟好之后，数组的起始位置已经固定了。我们不能想着将起始位置往前挪一格，然后留出来一个空位置进行插入；同样的也不能将起始位置往后挪一个就完成头删。

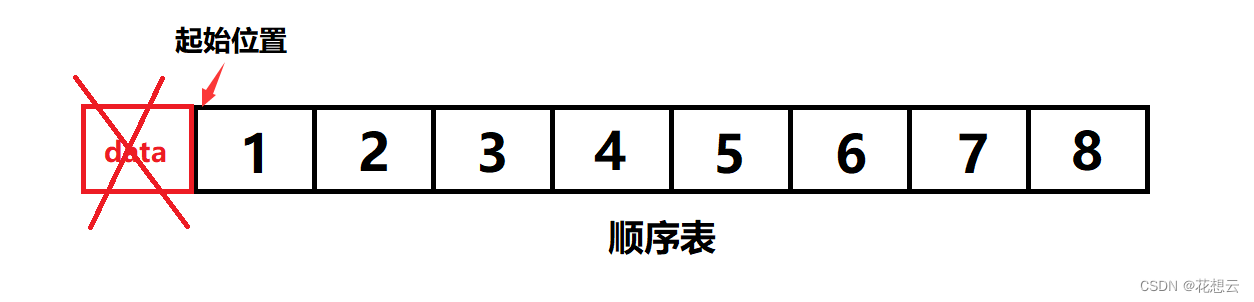
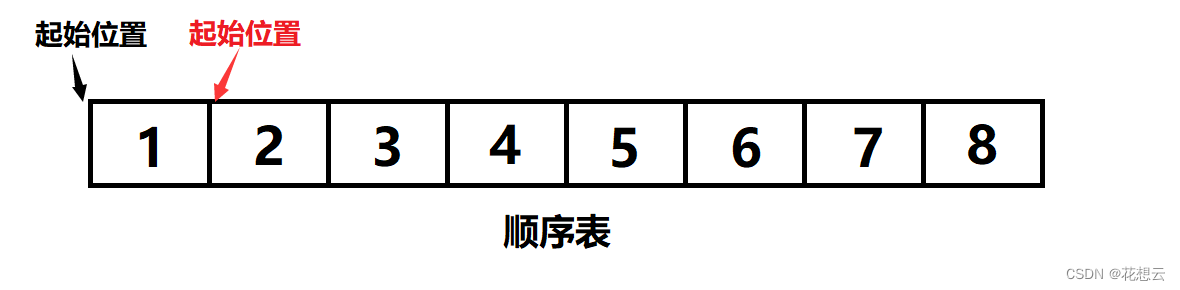
正确的头插与头删：

头插：从索引为0的位置开始，将所有数据向后平移一格，然后插入数据。

头删：从索引为1的位置开始，将所有数据向前平移一格，此时索引为0的位置的数据被索引为1的位置的数据覆盖掉了。

头插与头删关键的步骤是平移数据，因此头插与头删的时间复杂度为O(N)。

有关于数组更多详细的讲解，请参考这篇文章：

数据结构为何重要（数组）http://t.csdn.cn/NB1Uw

6.完整源码

SeqList.h文件

#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdbool.h>
#define N 5
typedef int SLDataType;//静态顺序表
typedef struct SeqList
{SLDataType a[N];//定长数组int size;//记录存储多少个有效数据
}SeqList;//初始化顺序表
void SLInit(SeqList* ps);
//静态顺序表的尾插
void SLPushBack(SeqList* ps,SLDataType data);
//静态顺序表的尾删
void SLPopBack(SeqList* ps);
//静态顺序表的头插
void SLPushFront(SeqList* ps,SLDataType data);
//静态顺序表的头删
void SLPopFront(SeqList* ps);
//pos位置插入数据
void SLInsert(SeqList* ps, int pos, SLDataType data);
//pos位置插入数据
void SLErase(SeqList* ps,int pos);
//查找数据
int SLFind(SeqList* ps, SLDataType data, int begin);
//判断数组是否已满
bool IsFull(SeqList* ps);
//打印存储的数据
void SLPrint(SeqList* ps);

SeqList.c文件

#define _CRT_SECURE_NO_DEPRECATE 1
#include"SeqList.h"void SLInit(SeqList* ps)
{assert(ps);ps->size = 0;
}void SLPushBack(SeqList* ps,SLDataType data)
{assert(ps);assert(!IsFull(ps));//插入数据ps->a[ps->size] = data;ps->size++;
}void SLPopBack(SeqList* ps)
{assert(ps);ps->size--;
}void SLPushFront(SeqList* ps, SLDataType data)
{assert(ps);assert(!IsFull(ps));//挪动数据for (int i = ps->size - 1; i >= 0; i--){ps->a[i + 1] = ps->a[i];}//插入数据ps->a[0] = data;ps->size++;
}void SLPopFront(SeqList* ps)
{assert(ps);assert(ps->size > 0);//挪动数据for (int i = 0; i < ps->size-1; i++){ps->a[i] = ps->a[i + 1];}ps->size--;
}void SLInsert(SeqList* ps, int pos, SLDataType data)
{assert(ps);assert(!IsFull(ps));//挪动数据for (int i = ps->size-1; i >= pos; i--){ps->a[i + 1] = ps->a[i];}//插入数据ps->a[pos] = data;ps->size++;
}void SLErase(SeqList* ps, int pos)
{assert(ps);assert(ps->size > 0);//挪动数据for (int i = pos; i < ps->size - 1; i++){ps->a[i] = ps->a[i + 1];}ps->size--;
}int SLFind(SeqList* ps, SLDataType data, int begin)
{assert(ps);assert(begin < ps->size);for (int i = begin; i < ps->size; i++){if (ps->a[i] == data){return i;}}return -1;
}void SLPrint(SeqList* ps)
{assert(ps);for (int i = 0; i < ps->size; i++){printf("%d ", ps->a[i]);}printf("\n");
}bool IsFull(SeqList* ps)
{assert(ps);if (ps->size == N){return true;}else{return false;}
}