---

一、最大团问题

1.1 问题描述

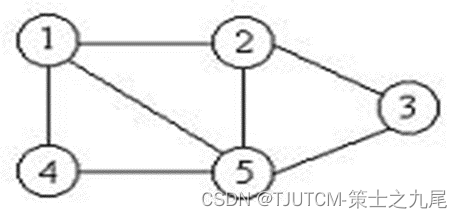
  给定无向图G=(V，E)。如果UV，且对任意u，vU有(u，v)E，则称U是G的完全子图。G的完全子图U是G的团当且仅当U不包含在G的更大的完全子图中。G的最大团是指G中所含顶点数最多的团。
  下图G中，子集{1，2}是G的大小为2的完全子图。这个完全子图不是团，因为它被G的更大的完全子图{1，2，5}包含。{1，2，5}是G的最大团。{1，4，5}和{2，3，5}也是G的最大团。

---

1.2 上界函数

  用变量cliqueSize表示 与该结点相应的团的顶点数；level表示 结点在子集空间树中所处的层次；用cliqueSize +n-level+1作为顶点数上界upperSize的值。
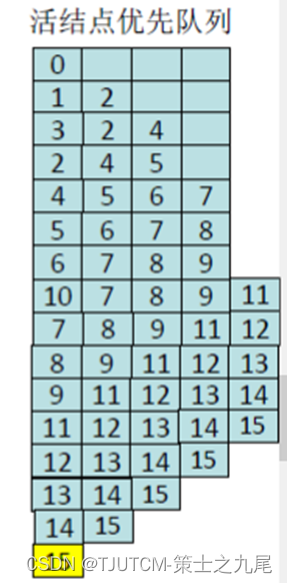
  在此 优先队列式分支限界法 中，upperSize实际上也是优先队列中元素的优先级。算法总是从活结点优先队列中抽取具有最大upperSize值的元素作为下一个扩展元素。

---

1.3 算法思想

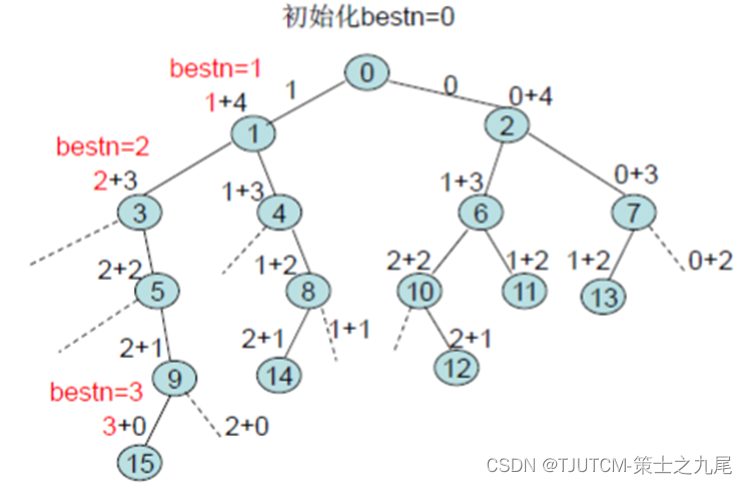
  子集树的根结点是初始扩展结点，对于这个特殊的扩展结点，其cliqueSize的值为0。
  算法在扩展内部结点时，首先考察其左儿子结点。在左儿子结点处，将顶点i加入到当前团中，并检查该顶点与当前团中其它顶点之间是否有边相连。当顶点i与当前团中所有顶点之间都有边相连，则相应的左儿子结点是可行结点，将它加入到子集树中并插入活结点优先队列，否则就不是可行结点。
  接着继续考察当前扩展结点的右儿子结点。当upperSize>bestn时，右子树中可能含有最优解，此时将右儿子结点加入到子集树中并插入到活结点优先队列中。

  算法的while循环的 终止条件 是遇到子集树中的一个叶结点(即n+1层结点)成为当前扩展结点。
  对于子集树中的叶结点，有upperSize＝cliqueSize。此时活结点优先队列中剩余结点的upperSize值均不超过当前扩展结点的upperSize值，从而进一步搜索不可能得到更大的团，此时算法已找到一个最优解。
  由于算法找到一个解就结束，所以无法找到该问题的所有解，这也是分支限界法的缺点！

  左子树：从顶点i到已选入的顶点集中每一个顶点都有边，否则剪枝。
  右子树：顶点数上界小于当前最优值（就是上面的bestn）时剪枝。
  顶点数上界=已确定的顶点数+未确定的顶点数的上界，以此作为优先队列中结点的优先级。

---

二、旅行售货员问题

2.1 问题描述

  某售货员要到若干城市去推销商品，已知各城市之间的路程(或旅费)。他要选定一条从驻地出发，经过每个城市一次，最后回到驻地的路线，使总的路程(或总旅费)最小。
  路线是一个 带权图。图中各边的费用（权）为正数。图的一条周游路线是包括V中的每个顶点在内的一条回路。周游路线的费用是这条路线上所有边的费用之和。
  旅行售货员问题的解空间可以组织成一棵树，从树的根结点到任一叶结点的路径定义了图的一条周游路线。旅行售货员问题要在图G中找出费用最小的周游路线。

---

2.2 算法描述

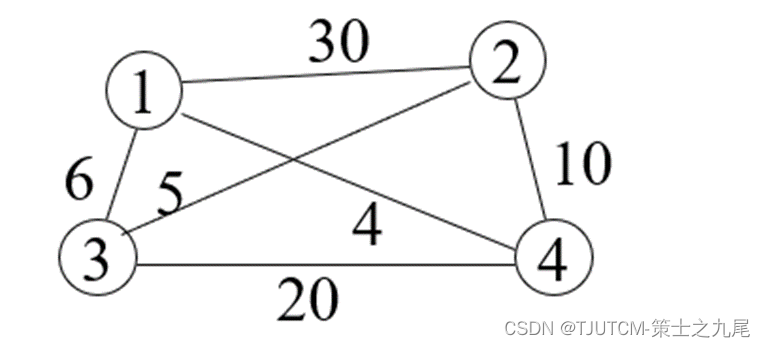
  算法开始时创建一个最小堆，用于表示 活结点优先队列。堆中每个结点的子树费用的下界lcost值是优先队列的优先级。接着算法计算出图中每个顶点的最小费用出边并用minout记录。如果所给的有向图中某个顶点没有出边，则该图不可能有回路，算法即告结束。如果每个顶点都有出边，则根据计算出的minout作算法初始化。
  算法的while循环体完成对排列树内部结点的扩展。对于当前扩展结点，算法分2种情况进行处理：
  1、首先考虑 s=n-2 的情形，此时当前扩展结点是排列树中某个叶结点的父结点。如果该叶结点相应一条可行回路且费用小于当前最小费用，则将该叶结点插入到优先队列中，否则舍去该叶结点。
  2、当 s<n-2 时，算法依次产生当前扩展结点的所有儿子结点。由于当前扩展结点所相应的路径是x[0:s]，其可行儿子结点是从剩余顶点x[s+1:n-1]中选取的顶点x[i]，且(x[s]，x[i])是所给有向图G中的一条边。对于当前扩展结点的每一个可行儿子结点，计算出其前缀(x[0:s]，x[i])的费用cc和相应的下界lcost。当lcost<bestc时，将这个可行儿子结点插入到活结点优先队列中。

  算法中while循环的终止条件是排列树的一个叶结点成为当前扩展结点。当s=n-1时，已找到的回路前缀是x[0:n-1]，它已包含图G的所有n个顶点。因此，当s=n-1时，相应的扩展结点表示一个叶结点。此时该叶结点所相应的回路的费用等于cc和lcost的值。剩余的活结点的lcost值不小于已找到的回路的费用。它们都不可能导致费用更小的回路。因此已找到的叶结点所相应的回路是一个最小费用旅行售货员回路，算法可以结束。
  算法结束时返回找到的最小费用，相应的最优解由数组v给出。

---

三、电路板排列问题

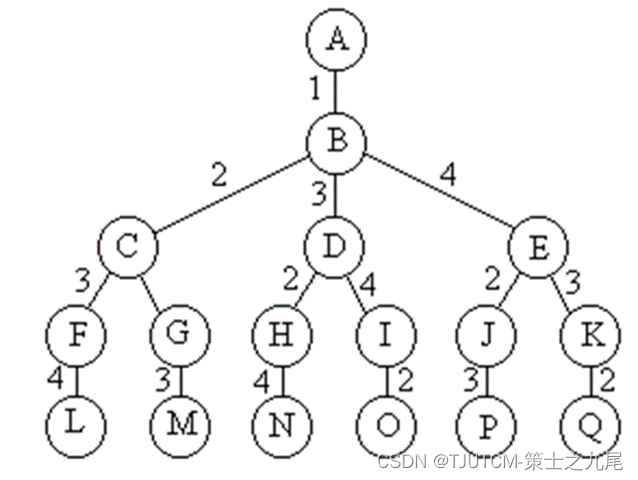
  将n块电路板以最佳排列方式插入带有n个插槽的机箱中。n块电路板的不同排列方式对应于不同的电路板插入方案。设B={1, 2, …, n}是n块电路板的集合，L={N1, N2, …, Nm}是连接这n块电路板中若干电路板的m个连接块。Ni是B的一个子集，且Ni中的电路板用同一条导线连接在一起。设x表示n块电路板的一个排列，即在机箱的第i个插槽中插入的电路板编号是x[i]。x所确定的电路板排列Density (x)密度定义为跨越相邻电路板插槽的最大连线数。

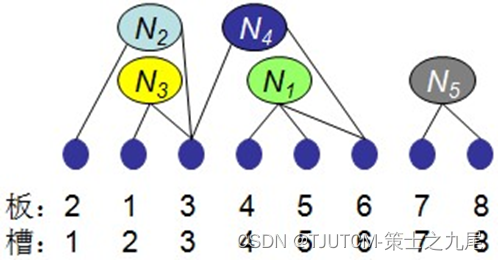
  例：如图，设n=8, m=5，给定n块电路板及其m个连接块：B={1, 2, 3, 4, 5, 6, 7, 8}，N1={4, 5, 6}，N2={2, 3}，N3={1, 3}，N4={3, 6}，N5={7, 8};其中两个可能的排列如图所示，则左电路板排列的密度是2。


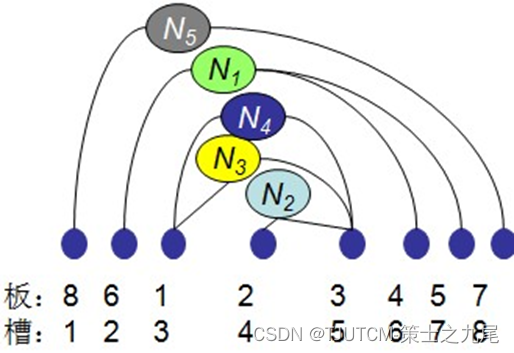
  在设计机箱时，插槽一侧的布线间隙由电路板的排列的密度确定。因此，电路板排列问题要求对于给定的电路板连接条件(连接块)，确定电路板的最佳排列，使其具有最小密度。
  电路板排列问题的 解空间是一颗排列树。采用优先队列式分支限界法找出所给电路板的最小密度布局。算法中采用最小堆表示活节点优先级队列。

---

3.1 算法描述

  算法开始时，将排列树的根结点置为当前扩展结点。在do-while循环体内算法依次从活结点优先队列中取出具有最小cd值的结点作为当前扩展结点，并加以扩展。
  首先考虑s=n-1的情形，当前扩展结点是排列树中的一个叶结点的父结点。x表示相应于该叶结点的电路板排列。计算出与x相应的密度并在必要时更新当前最优值和相应的当前最优解。
  当s<n-1时，算法依次产生当前扩展结点的所有儿子结点。对于当前扩展结点的每一个儿子结点node，计算出其相应的密度node.cd。当node.cd<bestd时，将该儿子结点N插入到活结点优先队列中。

do {// 结点扩展if (E.s == n - 1) {// 仅一个儿子结点int ld = 0; // 最后一块电路板的密度for (int j = 1; j <= m; j++)ld += B[E.x[n]][j];if (ld < bestd) {// 密度更小的电路板排列delete [] bestx;bestx = E.x;bestd = max(ld, E.cd);}

  S=n-1的情况，计算出此时的密度和bestd进行比较。

else{// 产生当前扩展结点的所有儿子结点for (int i = E.s + 1; i <= n; i++) {BoardNode N;N.now = new int [m+1];for (int j = 1; j <= m; j++)// 新插入的电路板N.now[j] = E.now[j] + B[E.x[i]][j];         

int ld = 0; // 新插入电路板的密度for (int j = 1; j <= m; j++)if (N.now[j] > 0 && total[j] != N.now[j]) ld++;N.cd = max(ld, E.cd);if (N.cd < bestd) {// 可能产生更好的叶结点//计算出每一个儿子结点的密度与bestd进行比较大于bestd时加入队列N.x = new int [n+1]; N.s = E.s + 1;for (int j = 1; j <= n; j++) N.x[j] = E.x[j]; N.x[N.s] = E.x[i]; N.x[i] = E.x[N.s]; H.Insert(N);}else delete [] N.now;}delete [] E.x;}

---

四、批处理作业调度问题

4.1 问题的描述

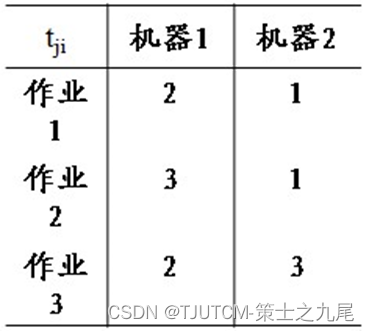
  给定n个作业的集合J={J1,J2,…,Jn}。每一个作业Ji都有2项任务要分别在2台机器上完成。每一个作业必须先由机器1处理，然后再由机器2处理。作业Ji需要机器j的处理时间为tji，i=1,2,…,n；j=1,2。对于一个确定的作业调度，设是Fji是作业i在机器j上完成处理的时间。则所有作业在机器2上完成处理的时间和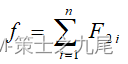 称为该作业调度的完成时间和。批处理作业调度问题要求对于给定的n个作业，制定最佳作业调度方案，使其完成时间和达到最小。

---

4.2 限界函数

  在结点E处相应子树中叶结点完成时间和的下界是：

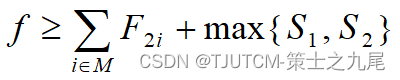
  注意到如果选择Pk，使t1pk在k>=r+1时依非减序排列，S1则取得极小值。同理如果选择Pk使t2pk依非减序排列，则S2取得极小值。

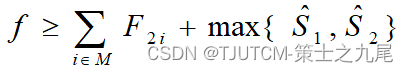
  这可以作为 优先队列式分支限界法中的限界函数。

---

4.3 算法描述

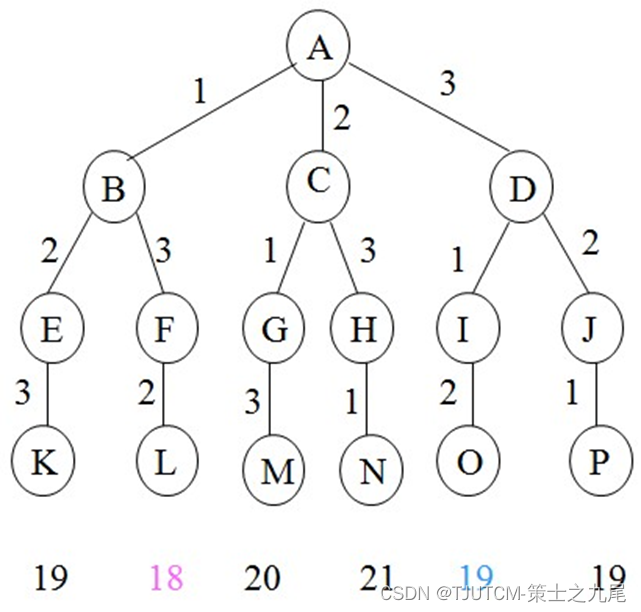
  算法的while循环完成对排列树内部结点的有序扩展。在while循环体内算法依次从活结点优先队列中取出具有最小bb值（完成时间和下界）的结点作为当前扩展结点，并加以扩展。
  首先考虑E.s=n的情形，当前扩展结点E是排列树中的叶结点。E.sf2是相应于该叶结点的完成时间和。当E.sf2 < bestc时更新当前最优值bestc和相应的当前最优解bestx。
  当E.s<n时，算法依次产生当前扩展结点E的所有儿子结点。对于当前扩展结点的每一个儿子结点node，计算出其相应的完成时间和的下界bb。当bb < bestc时，将该儿子结点插入到活结点优先队列中。而当bb bestc时，可将结点node舍去。

else {// 产生当前扩展结点的儿子结点for (int i = E.s; i < n; i++) {Swap(E.x[E.s],E.x[i]);int f1,f2;int bb=Bound(E,f1,f2,y);if (bb < bestc ) {//当bb<bestc时，将儿子结点插入到活结点优先队列中MinHeapNode N;N.NewNode(E,f1,f2,bb,n);H.Insert(N);}Swap(E.x[E.s],E.x[i]);}delete [] E.x;}  // 完成结点扩展

---

五、小结

  与回溯法非常相似，但采用广度优先或者最小代价优先
  下层结点可能优于上层节点扩展，到叶节点算法可以结束
  分支限界法适用于组合优化问题
  当前结点为根子树的可行解的上界或下界
  极大化与极小化问题的区别
  定义界的初值，得到新的更好的可行解就更新界

---

六、随机化算法

  现有一片不规则的树叶，如何在不使用微积分的情况下，求该叶片的面积，要求保留小数点后两位
  如果可以用微积分，只要获得叶片边缘曲线方程即可，无任何难度
  古人没有微积分，也能求出面积，而且很准，请问是如何求得的？
  求解的方法可以认为就是随机化算法