1.基本指令
部分指令,涉及到第4章的api,没有具体看实现,但是逻辑应该差不多。
zadd <key><score1><value1><score2><value2>...- 将一个或多个member元素及其score值加入到有序集key当中。
- 根据
zslInsert
zrange <key><start><stop>[WITHSCORES]- 返回有序集key中,下标在
之间的元素 - 根据
zslGetElementByRank以及backward指针
- 返回有序集key中,下标在
zrangebyscore key min max [withscores] [limit offset count]- 返回有序集 key 中,所有score值介于min和max 之间(包括等于min或max )的成员
- 根据
zslFirstInRange和zslLastInRange以及backward指针
zrank <key><value>- 返回该值在集合中的排名,从0开始。
- 根据
zslGetRank
2.数据结构
ZSET是由有序集合跳表实现的,按照分值的大小排序,分值相同时,按照成员对象的大小进行排序。同一个跳表可以有同分值的节点,但是对象必须是唯一的。
定义结构的代码src/server.h
// 1.ZSET节点
/* ZSETs use a specialized version of Skiplists */
typedef struct zskiplistNode {// member元素的valuesds ele;// member元素的scoredouble score;// 后向指针struct zskiplistNode *backward;// 层struct zskiplistLevel {// 前进指针struct zskiplistNode *forward;// 跨度unsigned long span;} level[];
} zskiplistNode;// 2.ZSET链表
typedef struct zskiplist {// 头节点和尾节点struct zskiplistNode *header, *tail;// 节点的数量(不包括头节点)unsigned long length;// 表中层数最大节点的层数int level;
} zskiplist;
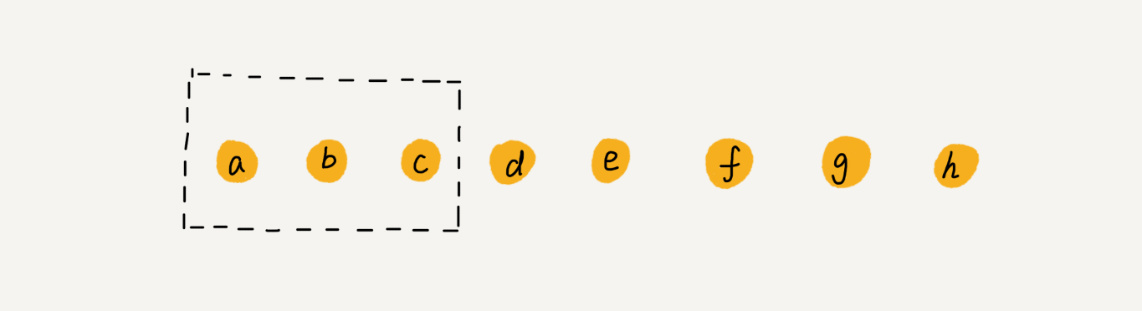
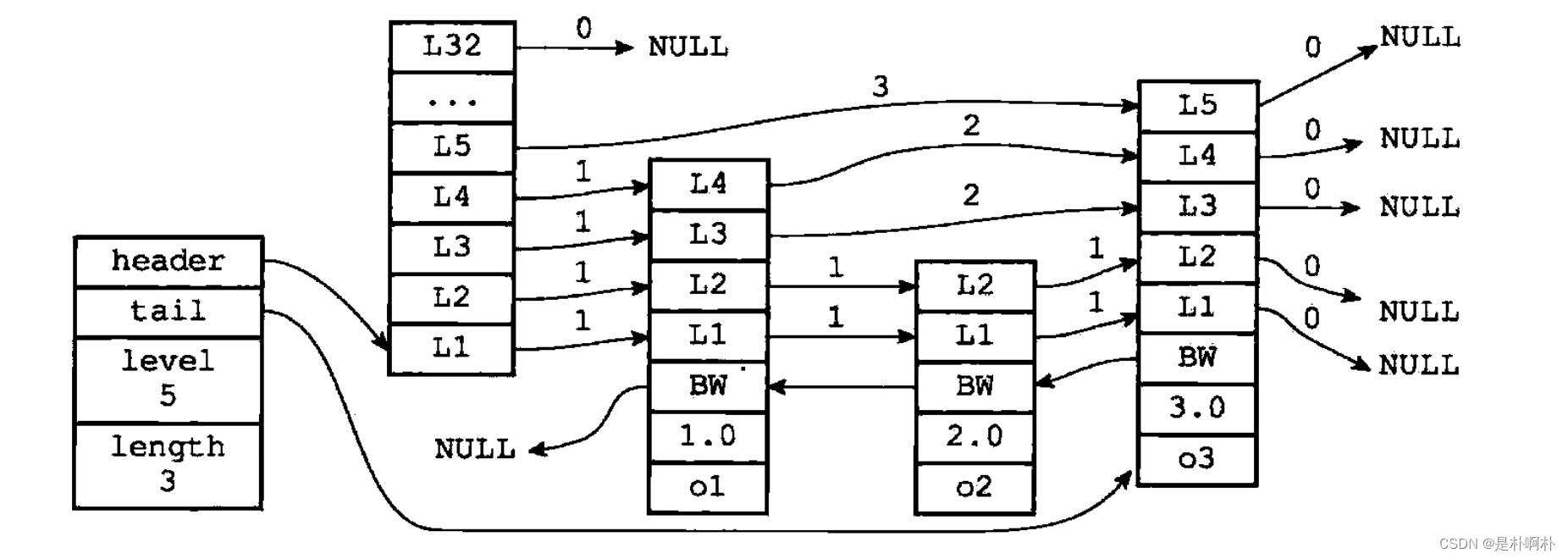
结合上方的图容易理解,其中有一些值得注意的点
- header表头节点只有level,没有存放元素的value和score。在zskiplist的length也不包括头节点。
- 每一层都有两个属性:前向forward指针和跨度。前向指针指向包含同一层的下一个结点,跨度记录了两个节点间的距离。指向NULL的跨度都为0。跨度是用来计算排位rank的,在查找某个节点的过程中,将沿途访问过的所有层跨度累计起来,就能得到目标节点的排位。
- 后向backward指针指向当前节点的前一个节点。目的是遍历。和range有关的指令,可以获得range范围的首尾节点后,从尾节点遍历到首节点。(只有backward指针是遍历相邻节点,forward指针每一层都有,指向的间隔为span的节点,不是下一个节点)
- 每次创建一个跳表节点时,根据幂次定律随机生成一个介于1到32之间的值作为level数组的大小。(见第3章节复杂度分析)
- 节点的score是一个double类型的浮点数,成员对象value是一个SDS(字符串对象)。如果想用zset实现两个维度排序,可以用拼接的思想。
3.跳表通用复杂度分析
跳表的复杂度和level的层数有关,如果只有一层,那复杂度必然都是最坏情况O(N)。一个节点有多少层来自于下面这个函数,在新建节点时,根据幂次定律生成一个1到32间的随机数。
可以理解为有概率P多加一层。
int zslRandomLevel(void) {static const int threshold = ZSKIPLIST_P*RAND_MAX;int level = 1;while (random() < threshold)level += 1;return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}
我们知道完全二叉树的复杂度推导是
2 h − 1 = N 2^h-1=N 2h−1=N
h = l o g 2 ( N + 1 ) h=log_2(N+1) h=log2(N+1)所以平均查找的时间复杂度是O(log(N))
跳表相当于一个多叉树,叉为 1 P \frac{1}{P} P1。(每一个节点有P的概率加一层,那相邻两层的节点数比为P。由于跳表最多32层,相邻两层实际节点数也不严格为P,所以这是一个近似的概念。)
复杂度推导为
( 1 P ) h − 1 − 1 = N (\frac{1}{P})^{h-1}-1=N (P1)h−1−1=N
h = l o g 1 p ( N + 1 ) h=log_{\frac{1}{p}}(N+1) h=logp1(N+1)
如果p=0.25, h = 0.5 ∗ l o g 2 ( N + 1 ) h=0.5*log_2(N+1) h=0.5∗log2(N+1)
如果p=0.5, h = l o g 2 ( N + 1 ) h=log_2(N+1) h=log2(N+1)
所以p在一定范围都是O(log(N))级别的复杂度。P在极端情况下(比如接近0或1)会变成O(N)。
推导比较粗糙,可能有问题
4.API复杂度分析
4.1. 查找元素
zslFirstInRange找到分值范围的第一个元素;zslLastInRange找到分值范围的最后一个元素
平均O(logN),最坏O(N)
zskiplistNode *zslFirstInRange(zskiplist *zsl, zrangespec *range) {zskiplistNode *x;int i;/* 判断跳表分数的范围是否在该范围内 */if (!zslIsInRange(zsl,range)) return NULL;x = zsl->header;/** 从最高的层数开始遍历,直到最底层 **/for (i = zsl->level-1; i >= 0; i--) {/* 在同一层通过前向指针遍历,直到下一个节点为空或者下一节点分数大于等于范围最小值,进入下一层 */while (x->level[i].forward &&!zslValueGteMin(x->level[i].forward->score,range))x = x->level[i].forward;}/* This is an inner range, so the next node cannot be NULL. *//* 下一节点就是目标值 */ x = x->level[0].forward;serverAssert(x != NULL);/* Check if score <= max. */if (!zslValueLteMax(x->score,range)) return NULL;return x;
}
int zslValueGteMin(double value, zrangespec *spec) {return spec->minex ? (value > spec->min) : (value >= spec->min);
}
4.2. 判断分值是否在范围
zslIsInRange判断是否至少一个节点的分值在范围内
O(1),根据头尾节点实现。zslFirstInRange和zslLastInRange都会先调用这个函数进行判断。
/* 存在返回1,不存在返回0 */
int zslIsInRange(zskiplist *zsl, zrangespec *range) {zskiplistNode *x;/* 对值的范围进行判定 */if (range->min > range->max ||(range->min == range->max && (range->minex || range->maxex)))return 0;// 1.获取尾节点,尾节点的分数不大于等于(就是小于)范围的最小值返回0x = zsl->tail;if (x == NULL || !zslValueGteMin(x->score,range))return 0;// 2.获取头节点,头节点的分数大于范围的最大值返回0x = zsl->header->level[0].forward;if (x == NULL || !zslValueLteMax(x->score,range))return 0;return 1;
}
4.3. 添加元素
zslInsert添加元素
平均O(logN),最坏O(N)
zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {/* 为了插入节点到正确位置,存储遍历过程中每一层最尽头的节点,其实就是新节点的上一个节点(该节点的forward指向新节点)*/zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;/* 为了更新span,存储遍历过程中每一层的rank */unsigned long rank[ZSKIPLIST_MAXLEVEL];int i, level;serverAssert(!isnan(score));/**和查找类似的思路**/x = zsl->header;for (i = zsl->level-1; i >= 0; i--) {/* 存储每一层的rank值 */rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];/* 在同一层通过前向指针遍历,直到1.下一个节点为空2.下一节点分数大于等于范围最小值3.节点分数相同元素值更大进入下一层 */while (x->level[i].forward &&(x->level[i].forward->score < score ||(x->level[i].forward->score == score &&sdscmp(x->level[i].forward->ele,ele) < 0))){/* 累加span获得rank */rank[i] += x->level[i].span;x = x->level[i].forward;}/* 记录每一层最末节点 */update[i] = x;}/* 获取一个随机的level层数 */level = zslRandomLevel();/* 如果新层数大于原跳表最大层数,更新zsl-level,并将超出的层记录下来 */if (level > zsl->level) {for (i = zsl->level; i < level; i++) {rank[i] = 0; update[i] = zsl->header;update[i]->level[i].span = zsl->length; }zsl->level = level; }x = zslCreateNode(level,score,ele);/* 更新新节点和每层新节点前一个节点的forward和span */for (i = 0; i < level; i++) {x->level[i].forward = update[i]->level[i].forward;update[i]->level[i].forward = x;/* update span covered by update[i] as x is inserted here */x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);update[i]->level[i].span = (rank[0] - rank[i]) + 1;}/* increment span for untouched levels *//* 高于该节点的每一个span因为插入了一个节点所以要增加1 */for (i = level; i < zsl->level; i++) {update[i]->level[i].span++;}/* 更新backward指针 */x->backward = (update[0] == zsl->header) ? NULL : update[0];if (x->level[0].forward)x->level[0].forward->backward = x;elsezsl->tail = x;zsl->length++;return x;
}
4.4.获取成员排位
zslGetRank返回包含给定成员和score的节点的排位
平均O(logN),最坏O(N)
unsigned long zslGetRank(zskiplist *zsl, double score, sds ele) {zskiplistNode *x;unsigned long rank = 0;int i;x = zsl->header;for (i = zsl->level-1; i >= 0; i--) {while (x->level[i].forward &&(x->level[i].forward->score < score ||(x->level[i].forward->score == score &&sdscmp(x->level[i].forward->ele,ele) <= 0))) {/* 这一步记录了rank */rank += x->level[i].span;x = x->level[i].forward;}/* x might be equal to zsl->header, so test if obj is non-NULL */if (x->ele && x->score == score && sdscmp(x->ele,ele) == 0) {return rank;}}return 0;
}
4.5. 获取某排位节点
zslGetElementByRank返回跳跃表在给定排位上的节点
zskiplistNode* zslGetElementByRank(zskiplist *zsl, unsigned long rank) {zskiplistNode *x;/* 记录了遍历过程中的rank累加值 */unsigned long traversed = 0; int i;x = zsl->header;for (i = zsl->level-1; i >= 0; i--) {while (x->level[i].forward && (traversed + x->level[i].span) <= rank){traversed += x->level[i].span;x = x->level[i].forward;}if (traversed == rank) {return x;}}return NULL;
}
参考
- 《redis的设计与实现》
- redis源码-7.2.1