对称二叉树
leetcode : https://leetcode.cn/problems/symmetric-tree/
参考 对称二叉树
递归思路
首先在开始时, 一定要注意, 对称二叉树对比的并不是一个节点的左右子树, 而是两棵树, 这个很关键!
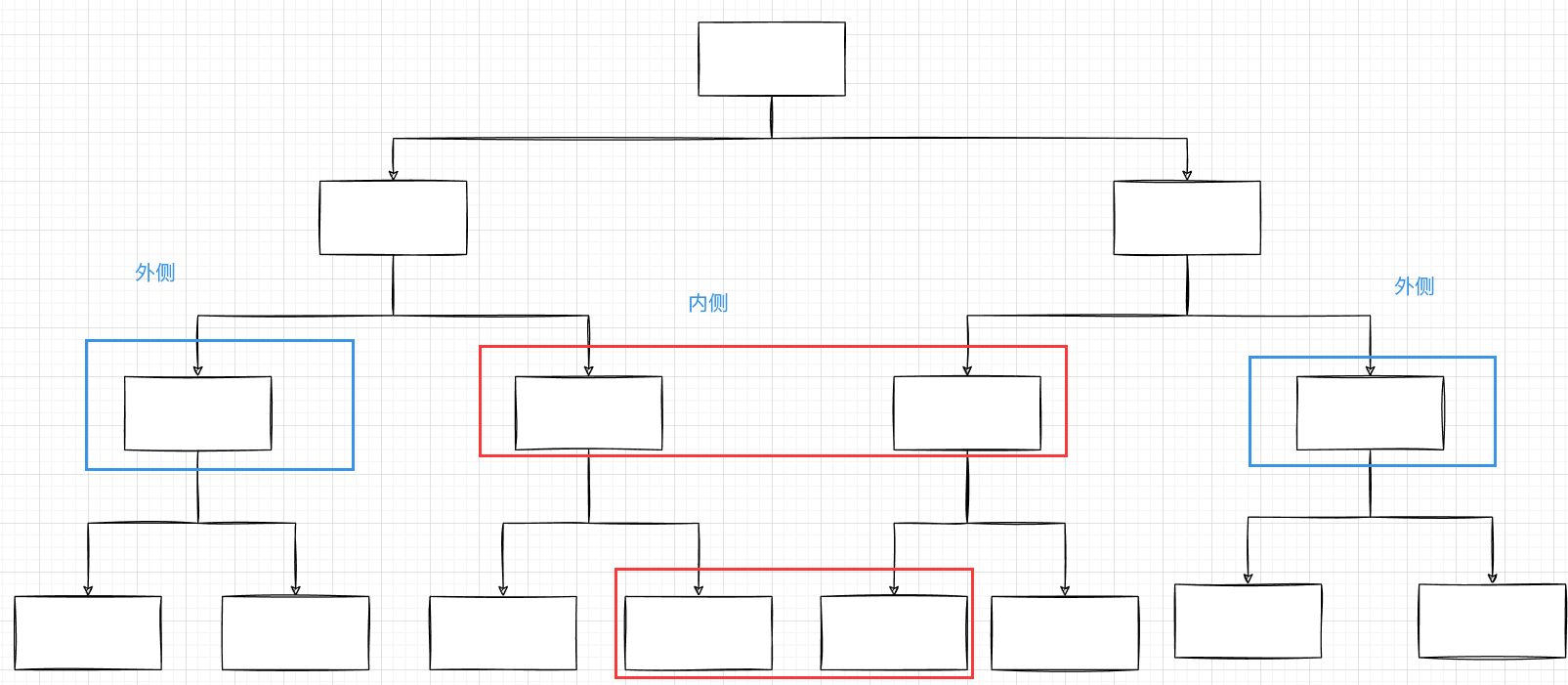
对比时是内侧和内侧对比, 外侧和外侧对比,
递归三步 :
-
确定递归的参数以及返回值
本题中需要去对比内侧和外侧节点是否对称, 所以返回值是 boolean 类型
private boolean compare(TreeNode left, TreeNode right) -
确定终止条件 :
-
我们在对比两棵树是否对称时, 主要分为以下几种情况
-
左节点为空, 右节点不为空, 不对称 (注意这里是左节点和右节点, 而不是左子树和右子树)
-
左节点不为空, 右节点为空, 不对称
-
左右节点都为空, 对称
-
左右节点都不为空, 此时要比较二者的值
-
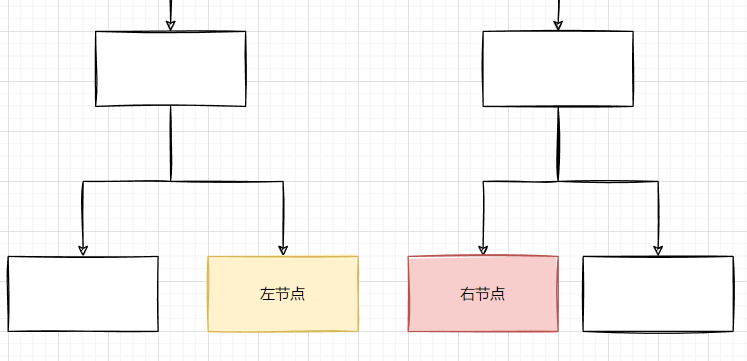
// 终止条件 : 避免操作空指针// 1. 左节点为空, 右节点不为空 不对称if(left == null && right != null) {return false;}// 2. 左节点不为空, 右节点为空 不对称if(left != null && right == null) {return false;}// 3. 左节点为空, 右节点为空 对称if(left == null && right == null) {return true;}
- 确定当前层逻辑
- 在确定了终止条件为空的情况下, 当前层的逻辑是 判断两个节点值是否相同
- 然后分别对比两棵树的内侧和外侧的节点
if(left.val != right.val) {return false;}// 1. 对比内侧boolean inside = compare(left.right, right.left);// 2. 对比外侧boolean outside = compare(left.left, right.right);return inside && outside;
递归流程
初始状态 : 传入 left 和 right
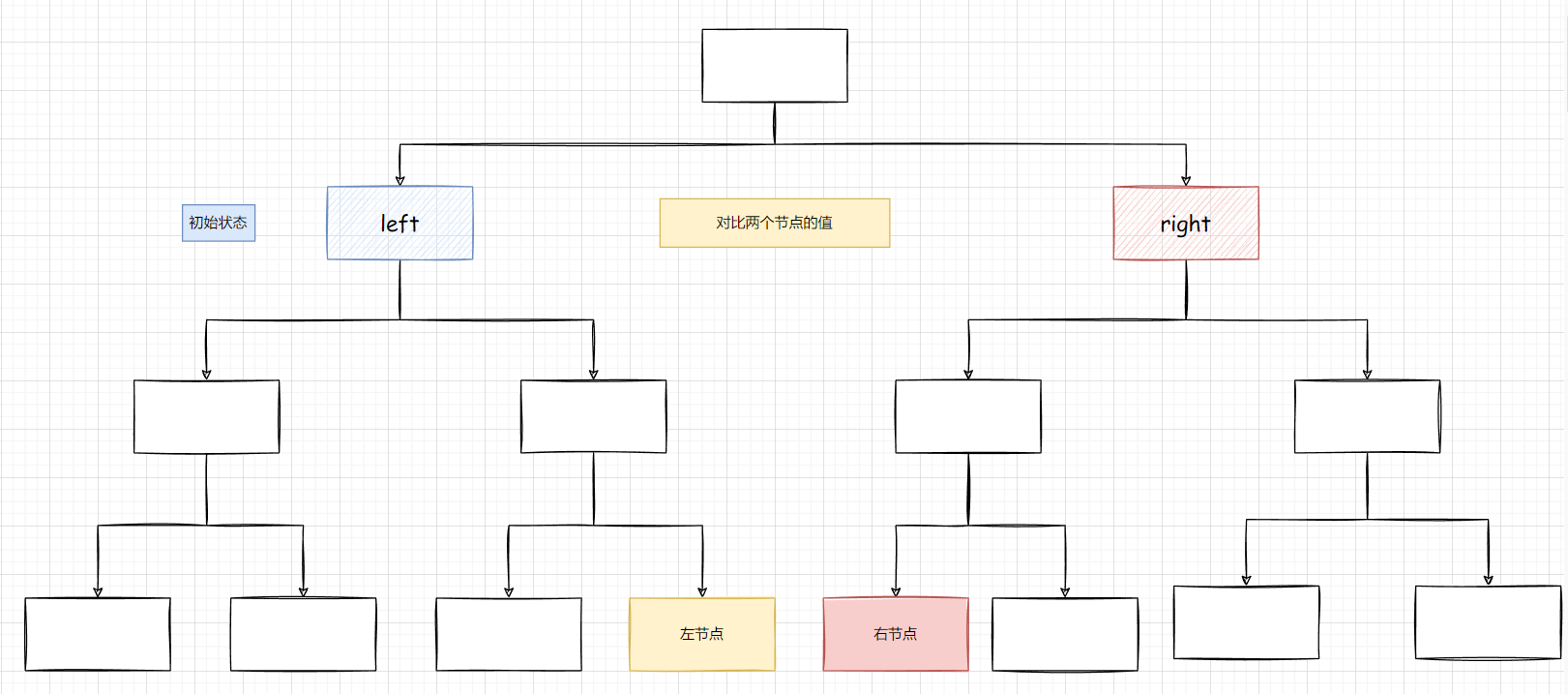
首先是会判断是否存在 left 或者 right 为空的情况(终止条件) , 这个也是为了防止处理空节点
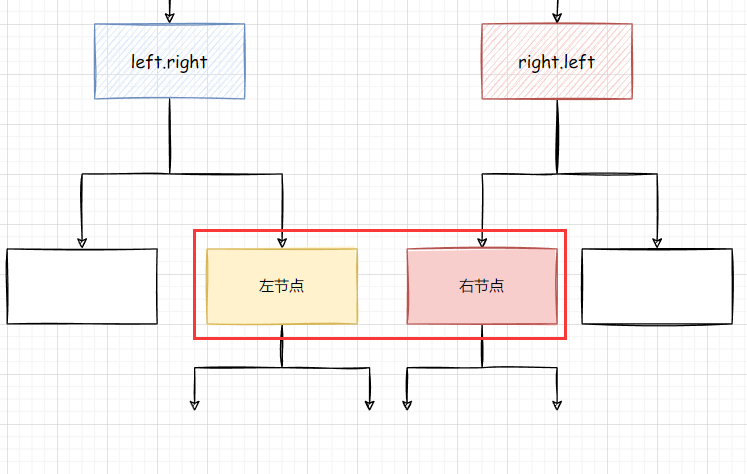
然后我们要对比以 left 为根节点 和 以right 为根节点的树, 如下图所示, 这个很关键
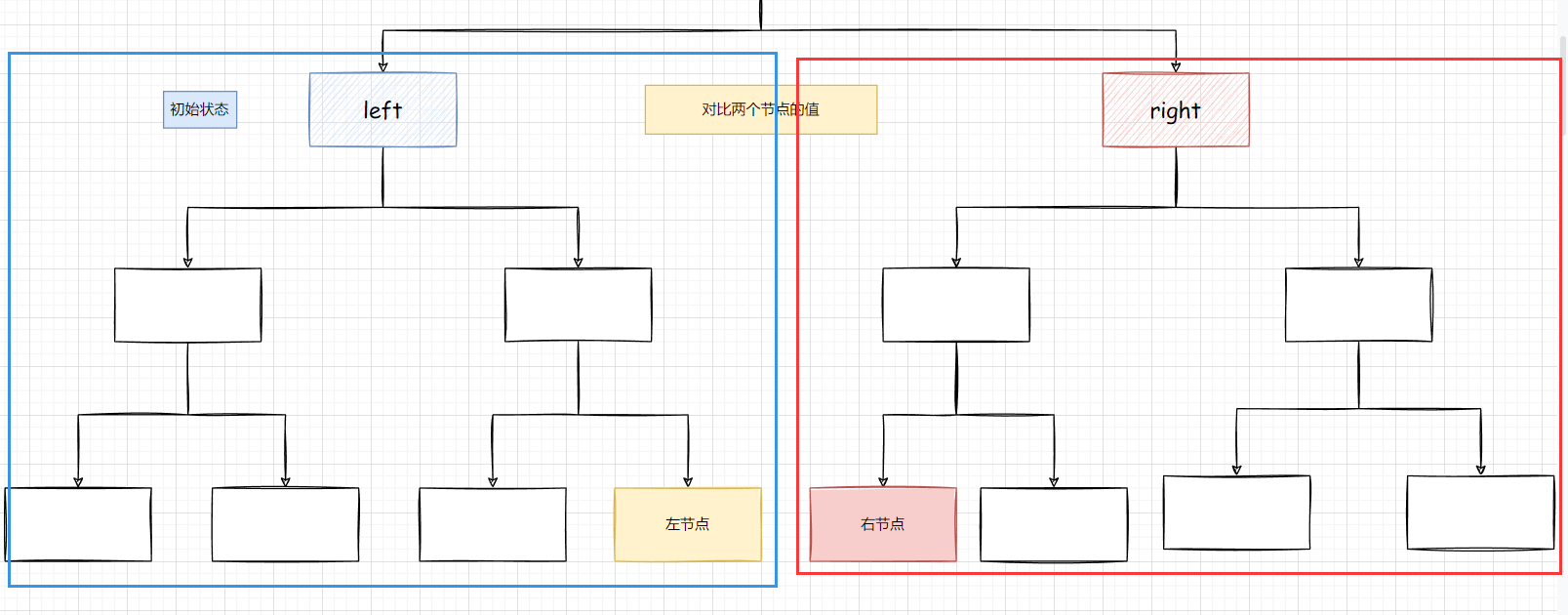
首先对比内侧的 :
boolean inside = compare(left.right, right.left);
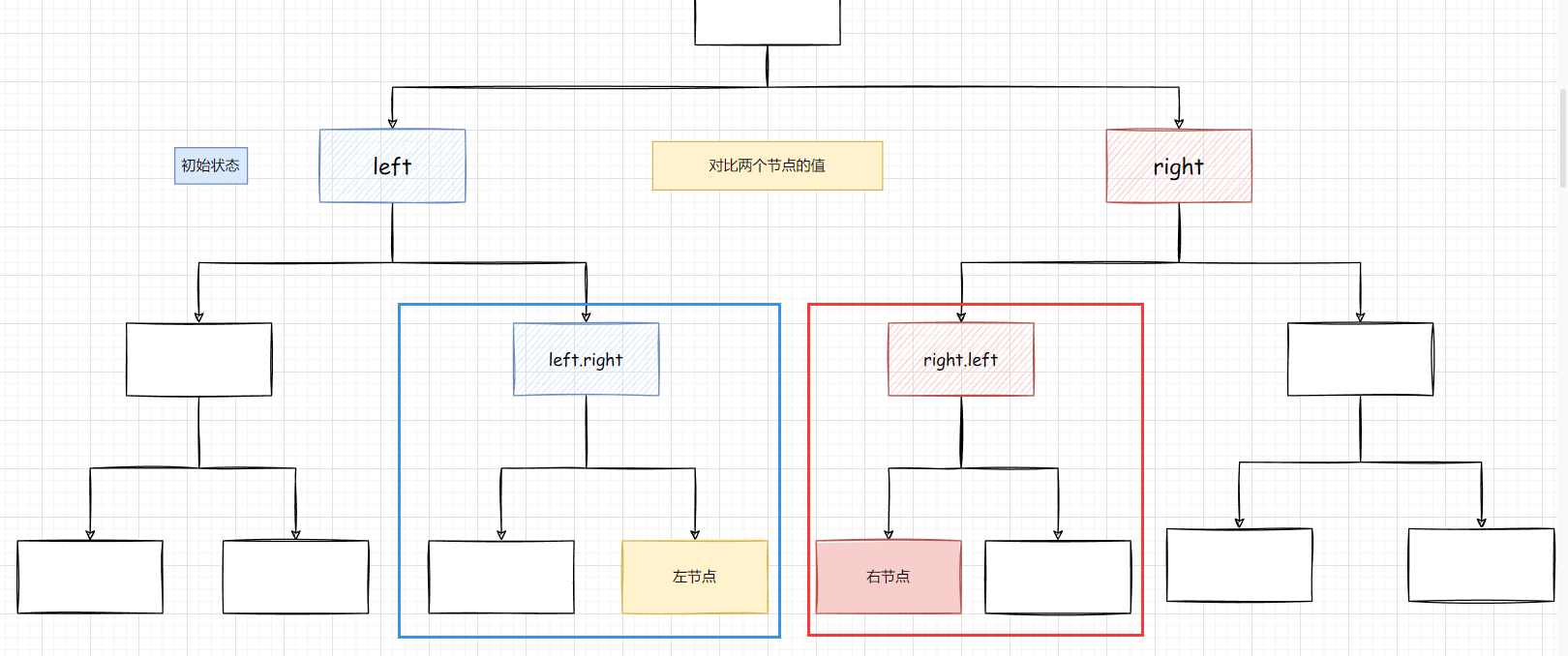
同理, 我们对比内侧其实就是对比的 left.right 和 right.left 这两棵子树是否对称
我们假设, 当前的树不再向下延伸(这棵树就这么大), 此时的逻辑是
-
先判断是否满足终止条件, 也就是存在 left.right 或者 right.left 为空的情况, 此时不对称, 直接就返回结果了
boolean inside = compare(left.right, right.left);inside = false , 直接结束
-
假设没有到达终止条件, 先比较 left.right.val 和 right.left.val 是否相等
-
比较内侧和外侧的节点是否对称
-
最后会返回 left.right 和 right.left 这两棵树的是否对称的结果
需要补充的是, 当最后到达叶子节点时, 其实叶子节点也可以看做左右子节点都为空的树
如上图所示, 此时他们会被下面的代码处理
// 3. 左节点为空, 右节点为空 对称if(left == null && right == null) {return true;}
递归代码
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isSymmetric(TreeNode root) {return compare(root.left, root.right);}private boolean compare(TreeNode left, TreeNode right) {// 终止条件 : 避免操作空指针// 1. 左节点为空, 右节点不为空 不对称if(left == null && right != null) {return false;}// 2. 左节点不为空, 右节点为空 不对称if(left != null && right == null) {return false;}// 3. 左节点为空, 右节点为空 对称if(left == null && right == null) {return true;}// 当前层的处理逻辑 : 左右子树都不为空if(left.val != right.val) {return false;}// 下一层// 1. 对比内侧boolean inside = compare(left.right, right.left);// 2. 对比外侧boolean outside = compare(left.left, right.right);return inside && outside;}}
迭代思路
迭代思路和递归思路有一些相似, 都是外侧和外侧对比, 内侧和内侧对比 !
核心的点就是把每一层的取出来, 然后按照 内侧对内侧 和 外侧对外侧的顺序存入队列
这样的话, 每次取出栈顶的两个都是一对的
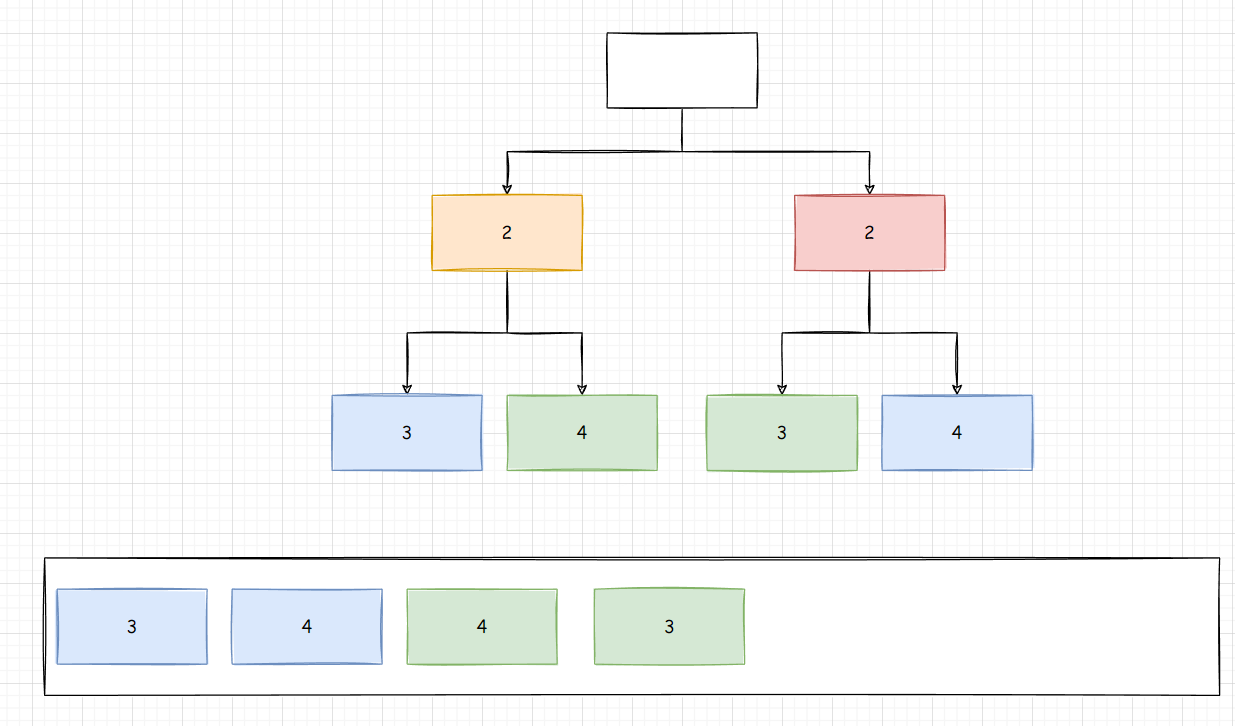
如上图, 核心点是存入队列的时候, 存入的顺序是成对的!
因为取出来正好的成对的, 这样取出节点后, 我们只需要判断是否对称即可
- 左右节点都为空, 不处理, 直接跳过 (对称)
- 左节点为空, 右节点不为空 (不对称)
- 左节点不为空, 右节点为空 (不对称)
- 左右节点都不为空, 比较两个节点的值是否相同
迭代代码
需要注意的是 , LinkedList 是可以存储null值的, 其他的数据结构不一定支持
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isSymmetric(TreeNode root) {Queue<TreeNode> queue = new LinkedList<>();queue.add(root.left);queue.add(root.right);while(!queue.isEmpty()) {TreeNode left = queue.poll();TreeNode right = queue.poll();// 判断// 1. 左空, 右不空, 不对称if(left == null && right != null ) {return false;}// 2. 左不为空, 右为空 不对称if (left != null && right == null) {return false;}// 左右都为空, 就不处理if(left == null && right == null) {continue;}// 左右都不为空的情况, 比较二者的值if(left.val != right.val) {return false;}// 将下一层子节点添加到队列// 注意, 要按照对称的顺序, 外侧对外侧, 内侧对内侧// left.left 和 right.right// left.right 和 right.left// 外侧queue.add(left.left);queue.add(right.right);// 内侧queue.add(left.right);queue.add(right.left);}return true;}
}