一.理论基础

二.遍历顺序问题

2.1 01背包

2.2完全背包

3.相关题型

3.1零钱兑换

3.1.数组总和IV

一.理论基础

题目描述：

有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

例如，假设背包的最大重量是4

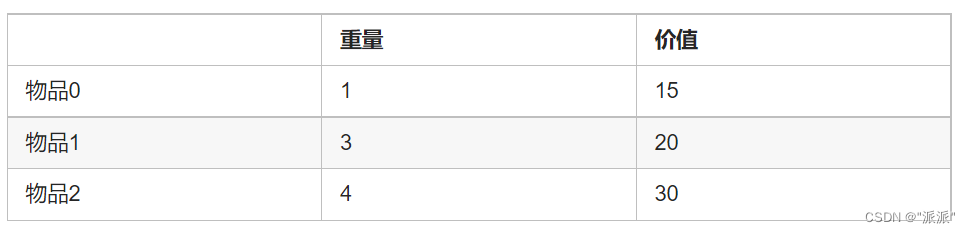
先来看下01背包问题的核心代码：

for (int i = 0; i < weight.size(); i++) // 遍历物品
{                                 for (int j = bagWeight; j >= weight[i]; j--) {dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); // 遍历背包容量}
}

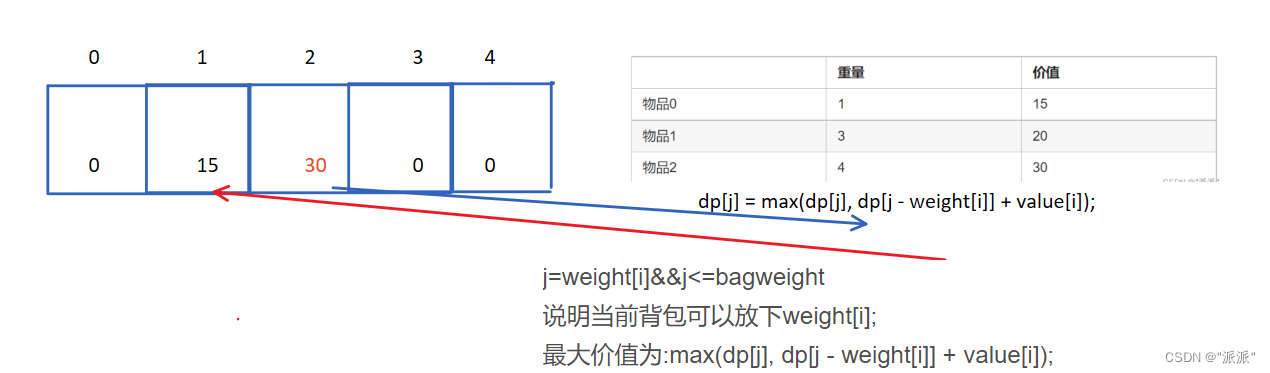
这是一维dp数组，因为每个物品只能够放一次，所以在遍历背包容量时要从大到小去遍历。这就很容易想到了，在遍历完全背包时，由于每个相同物品可以放入多次，所以再遍历背包容量时应该从小到大去遍历。例如：

for (int i = 0; i < weight.size(); i++) // 遍历物品
{                                 for (int j = weight[i]; j <=bagweight; j++) {dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); // 遍历背包容量}
}

二.遍历顺序问题

2.1 01背包

先简单说下01背包遍历的顺序问题。当使用二维数组去遍历的时候，遍历背包容量时是从小到大遍历的。例如：（当时是先遍历物品，再遍历背包）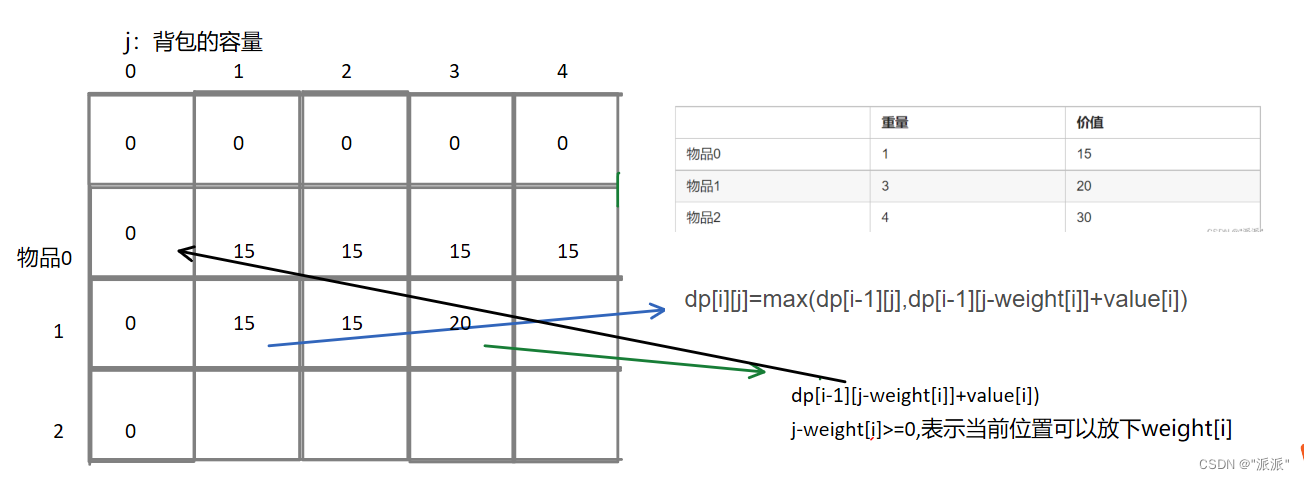

用二维数组时，也是可以先遍历背包容量，再去遍历物品。每次遍历所要用到的数据都是来自当前位置的左上角（包括左边和正上边）。虽然两个for循环遍历的次序不同，但是dp[i][j]所需要的数据就是左上角，根本不会影响dp[i][j]公式的推导。例如：

for (int j = 0; j <= bagWeight; j++)      // 遍历背包容量
{                   for (int i = 1; i < weight.size(); i++)   // 遍历物品{                                    if (j < weight[i]) dp[i][j] = dp[i - 1][j];elsedp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}
}

如果用一维数组呢？

前面已经说了，用一维数组模拟01背包问题时，遍历背包容量时是要从大到小去遍历，才能确保每个物品放了一次。（前面是先遍历物品，后面遍历背包的），那么遍历顺序是否可以改变呢？

答案肯定不能，例如：

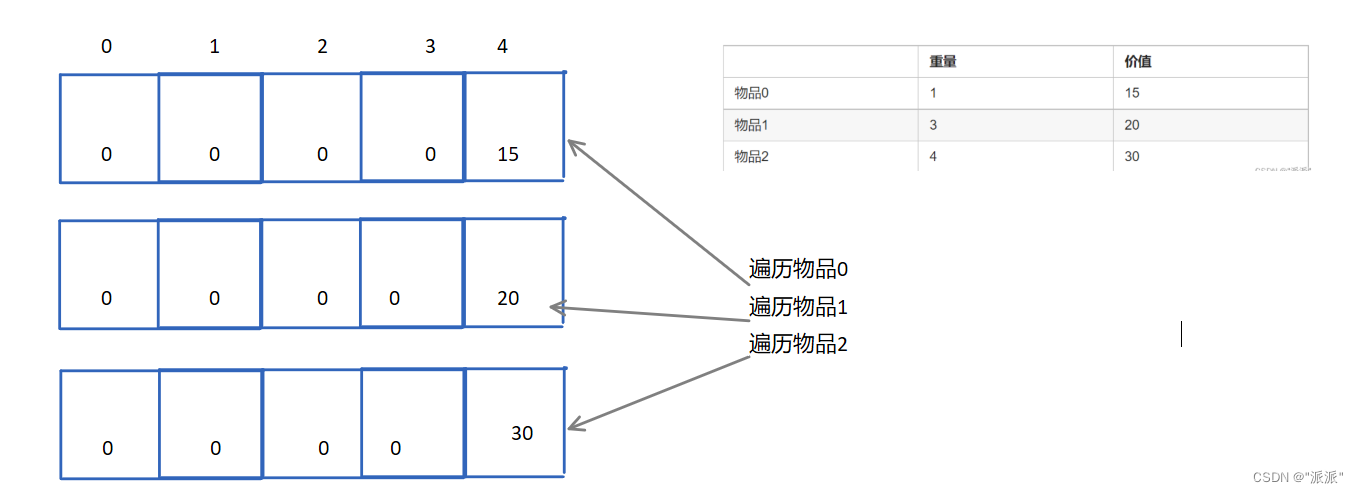
会发现每次背包只放了一个物品。

2.2完全背包

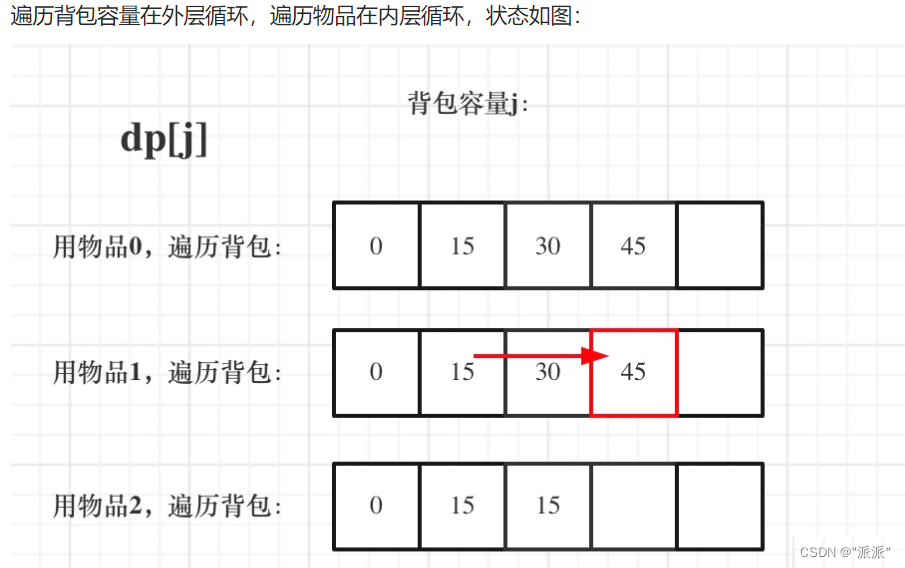
先看一维数组的遍历顺序，前面是先遍历物品，在遍历背包容量（遍历背包容量时是从小到大，才能确保同一个物品可以放入多次）。

例如：

for (int i = 0; i < weight.size(); i++) // 遍历物品
{                                 for (int j = weight[i]; j <=bagweight; j++) {dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); // 遍历背包容量}
}

遍历顺序：

如果先遍历背包容量，再去遍历物品也是可以的：

代码：

for (int j = 0; j <= bagWeight; j++) // 遍历背包容量
{for (int i = 0; i < weight.size(); i++)// 遍历物品{ if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}

3.相关题型

3.1零钱兑换

题目描述：

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

例如：

输入：amount = 5, coins = [1, 2, 5]
输出：4
解释：有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

思路：硬币的面额对应的是物品，凑成的总金额是背包容量。问把背包容量放满，有几种组成方式。价值对应的就是不同的组合方式。例如：

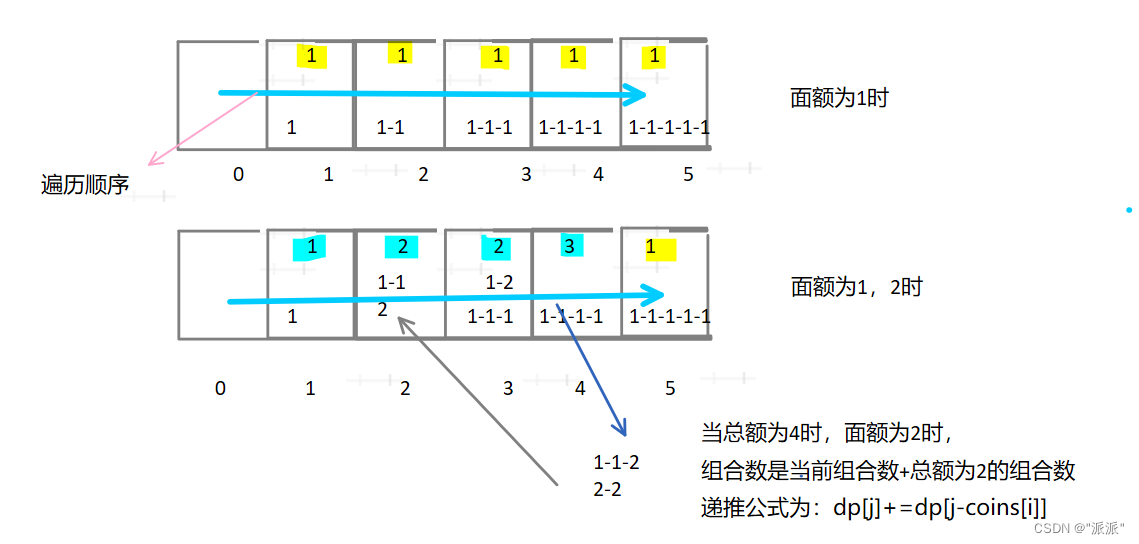
那么初始化时将dp[0]初始化为1即可。注意（上面是先遍历物品，再遍历背包）

代码：

class Solution {
public:int change(int amount, vector<int>& coins) {vector<int>dp(amount+1,0);dp[0]=1;for(int i=0;i<coins.size();i++){for(int j=1;j<=amount;j++){if(j>=coins[i])//说明当前可以有一种组合满足,此时背包容量为j，刚好放满{dp[j]+=dp[j-coins[i]]; //当前的组合数+背包容量为j-coins[i] 的组合数}}}return dp[amount];  //遍历完所有物品}
};

先遍历背包容量，再遍历物品可以么？还是看图，其实算出的是排列数（也就是面额顺序不同即可）

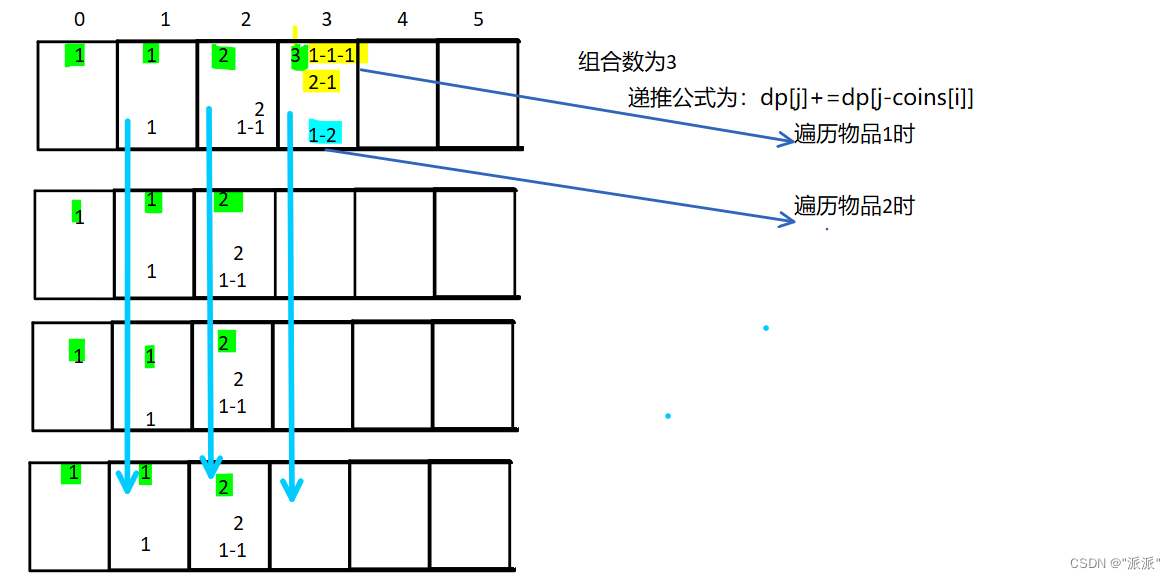
3.1.数组总和IV

题目描述：

给你一个由不同整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。

例如：

输入：nums = [1,2,3], target = 4
输出：7
解释：
所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)

跟上面那题一样的吧，不过求的是排列数，直接上代码吧

class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<double> v(target+1,0);v[0]=1;for(int i=1;i<=target;i++)  //先遍历背包{for(int j=0;j<nums.size();j++)  //再遍历物品{if(i>=nums[j])v[i]+=v[i-nums[j]];}}return v[target];}
};