劳资博弈
0 引言
前一篇文章介绍了静态博弈中常见的几个案例以及场景,并且在此之前也还介绍过斯塔克尔伯格博弈等动态博弈,以及相关的解决方法——反应函数法。今天我们继续介绍一个常见的动态博弈——劳资博弈,并利用反应函数解决!
1 劳资博弈
劳资博弈是一个工会和厂商之间的博弈模型。该模型假设工资完全由工会决定,厂商决定雇佣工人的数量,博弈过程是(1)先由工会决定工资率,(2)然后厂商决定雇佣多少工人。
注意,工会代表的是工人群体,其不只追求较高的工资,还会希望较多的工人得到雇佣,高工资加高失业率不符合工会利益,低工资实现的高就业也不符合工会利益。因此,工会的效用(utility)是工资率和雇佣工人数两者的函数 u = u ( W , L ) u=u(W,L) u=u(W,L)。其中,W和L分别表示工资率(可理解为单位成本)和厂商雇佣工人数。为了简便起见,假设工资率和雇佣数都连续可分,即W、L是连续型变量。
假设厂商只关心利润,利润是收益和成本之差。假设收益是关于工人数的函数 R ( L ) R(L) R(L),再假设只有劳动成本,总成本C等于工资率乘以工人数
C = W × L C=W×L C=W×L
则厂商的利润函数是关于工资率以及工人人数的函数:
π = π ( W , L ) = R ( L ) − W L π=π(W,L)=R(L)-WL π=π(W,L)=R(L)−WL
用逆推归纳法分析这个博弈。
(1)第一步先分析第二阶段厂商的选择,也就是厂商对工会选择的工资率W的反应函数L(W)。
厂商实现自己最大得益(利润)的雇佣工人数L是以下最大值问题的解:
m a x L ≥ = 0 π ( W , L ) = m a x L ≥ = 0 ( R ( L ) − W L ) \underset{L≥=0}{max}π(W,L)= \underset{L≥=0}{max}(R(L)-WL) L≥=0maxπ(W,L)=L≥=0max(R(L)−WL)
将上述函数对L求偏导得:
∂ π ( W , L ) ∂ L = R ′ ( L ) − W \frac{∂π(W,L)}{∂L}=R'(L)-W ∂L∂π(W,L)=R′(L)−W
令 ∂ π ( W , L ) / ∂ L = 0 ∂π(W,L)/∂L=0 ∂π(W,L)/∂L=0得:
R ′ ( L ) = W R'(L)=W R′(L)=W
即能使该等式成立的L便是厂商实现最大利润的雇佣工人数,也就是给定工会选择的工资率W时厂商的最优雇佣工人数。
(2)第二步回到第一阶段工会的选择。
工会了解厂商的决策方法,完全清楚对应自己选择的每种工资率W,厂商将会根据上述方式决定雇佣数 L ∗ ( W ) L^* (W) L∗(W)。因此,工会的决策问题是选择 W ∗ W^* W∗,使它是下列最大值函数的解:
m a x W ≥ = 0 π [ W , L ∗ ( W ) ] \underset{W≥=0}{max}π[W,L^* (W)] W≥=0maxπ[W,L∗(W)]
在不给出 π ( W , L ) π(W,L) π(W,L)、 R ( L ) R(L) R(L)等具体函数时,给模型得这里已经求解完毕,接下来我们结合图像对该模型进一步进行解释!
2 图像
我们继续研究 R ′ ( L ) = W R' (L)=W R′(L)=W,它的经济意义是厂商增加雇佣的边际收益,也就是雇佣最后一单位劳动增加的收益,等于雇佣一单位劳动的边际成本(W),本模型中也是平均成本,即工资率。
首先以L为横坐标,R为纵坐标建立坐标系:
(1)可以绘制WL是该坐标系上过原点的,以W为斜率的射线(L≥0);
(2)假设R(L)不是直线,而是曲线:
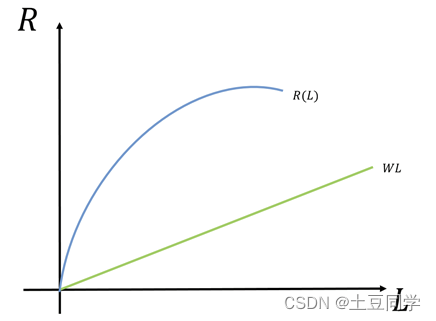
R ′ ( L ) = W R'(L)=W R′(L)=W的几何意义为,当曲线R(L)的斜率等于W,也就是说当曲线R(L)在某点 L ∗ L^* L∗上的切线与WL平行时,此时的该点的横坐标 L ∗ L^* L∗便是厂商实现最大利润的雇佣工人数,也就是给定工会选择的工资率W时厂商的最优雇佣工人数 L ∗ ( W ) L^* (W) L∗(W)。
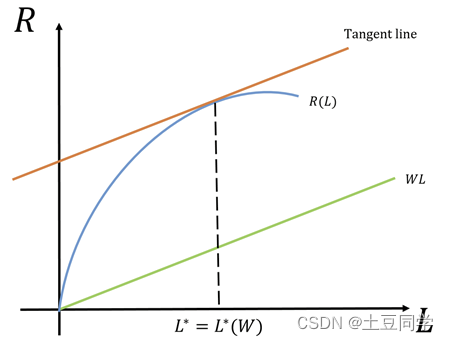
此时, R ( L ∗ ) R(L^*) R(L∗)的切线与WL平行,即在 L ∗ = L ∗ ( W ) L^*=L^* (W) L∗=L∗(W)处,R(L)与WL之间距离 R ( L ) − W L R(L)-WL R(L)−WL(厂商的利润)最大!
3 实例验证
假设厂商收益函数 R ( L ) = 10 L − L 2 R(L)=10L-L^2 R(L)=10L−L2,则根据
∂ π ( W , L ) ∂ L = R ′ ( L ) − W = 0 \frac{∂π(W,L)}{∂L}=R' (L)-W=0 ∂L∂π(W,L)=R′(L)−W=0
可得:
10 − 2 L − W = 0 10-2L-W=0 10−2L−W=0
进一步得:
L ∗ ( W ) = ( 10 − W ) / 2 L^* (W)=(10-W)/2 L∗(W)=(10−W)/2
再假设
π ( W , L ) = W 1 / 2 L 1 / 2 π(W,L)=W^{1/2}L^{1/2} π(W,L)=W1/2L1/2
则
π [ W , L ∗ ( W ) ] = W 1 / 2 ( 10 − W 2 ) 1 / 2 = ( 10 W − W 2 2 ) 1 / 2 π[W,L^* (W)]=W^{1/2} (\frac{10-W}{2})^{1/2}=(\frac{10W-W^2}{2})^{1/2} π[W,L∗(W)]=W1/2(210−W)1/2=(210W−W2)1/2
求 π [ W , L ∗ ( W ) ] π[W,L^* (W)] π[W,L∗(W)]最大值即求 ( 10 W − W 2 ) / 2 (10W-W^2)/2 (10W−W2)/2的最大值,令其一阶导为0可得:
10 − 2 W = 0 ⇒ W ∗ = 5 10-2W=0⇒W^*=5 10−2W=0⇒W∗=5
进一步得到
L ∗ ( W ∗ ) = ( 10 − 5 ) / 2 = 2.5 L^* (W^* )=(10-5)/2=2.5 L∗(W∗)=(10−5)/2=2.5
所以 ( W , L ) = ( 5 , 2.5 ) (W,L)=(5,2.5) (W,L)=(5,2.5)是该博弈的子博弈完美纳什均衡!





![[论文笔记]UNILM](https://img-blog.csdnimg.cn/img_convert/2d1261c204cbcbe50002d7933098b7ce.png)