0. 简介

在面对二维与三维之间的转换时，我们常常会困惑该如何去转换，在G2O中存在有理想的坐标转换工具，但是在Sophus中却缺乏这样的手段。之前在Sophus处简要的介绍了一下SE(2)与SE(3)的转换，最近发现之前的文章这部分需要拿出来详细的说一说。

1. 欧拉角与旋转向量

欧拉角、旋转向量、四元数和旋转矩阵是Sophus中常常提到的几个名词，欧拉角和旋转向量是类似的，SO(3)的旋转矩阵有9个量，但是只有3个自由度，并且是单位正交矩阵，具有冗余性，对其估计或优化问题的求解不方便。我们可以用一个旋转轴和一个旋转角描述任意旋转。一个方向与旋转轴一致，长度（模）等于旋转角的向量，我们称之为旋转向量(或轴角)。

旋转向量到旋转矩阵：

$R=cos\theta I+(1-cos\theta )n{n}^T+sin\theta \hat{n}$

其中提到的$\hat{n}$是向量的旋转矩阵，由于是反对称矩阵，所以只存在三个自由度，我们可以$X-Y-Z$轴来规定其反对称矩阵轴:
$\hat{n}=\left[\begin{array}{ccccc}0& & -n_z& & n_y\\ n_z& & 0& & -n_x\\ -n_y& & n_x& & 0\end{array}\right]$

所以我们可以从se,so中得到旋转向量数值。而欧拉角对于轴角表示情况,转轴具有2个自由度,转角1个自由度。 根据三次基本转动选取的坐标轴的不同，欧拉角共有12种组合。如 果再考虑到可选取原始坐标系的坐标轴，也可选取“新”坐标系的坐标轴，则共有24种欧拉角表示。一般规定原始坐标系为静坐标系，每个基本转动后形成的新坐标系为动坐标系。

• 24 种欧拉角表示列举如下：
• 静轴(即转轴选静坐标系的坐标轴):
  $sXYZ,sXZY,sXYX,$
  $sXZX,sYXZ,sYZX,$
  $sYXY,sYZY,sZXY,$
  $sZYX,sZXZ,sZYZ$

动轴(即转轴选动坐标系的坐标轴):

$rZYX,rYZX,rXYX,$
$rXZX,rZXY,rXZY,$
$rYXY,rYZY,rYXZ,$
$rXYZ,rZXZ,rZYZ$

静轴欧拉角和动轴欧拉角有如下规律:
绕静轴 $XYZ$ 分别 转 $\alpha ,\beta ,\gamma$ 角度的转动与绕动轴 $ZYX$分别转 $\gamma ,\beta ,\alpha$ 角度的转动等价，其他形式的欧拉角亦有此类似规律。

对于不同的坐标系定义，有不同的转换关系。我们只讨论常用的一种情况：如上图，右手系，Z轴朝上，X轴朝前，y轴朝左。绕Z轴作偏航（Yaw）运动，绕Y轴作俯仰（Pitch）运动，绕X轴作滚转（Roll）运动，运动正方向如上图所示。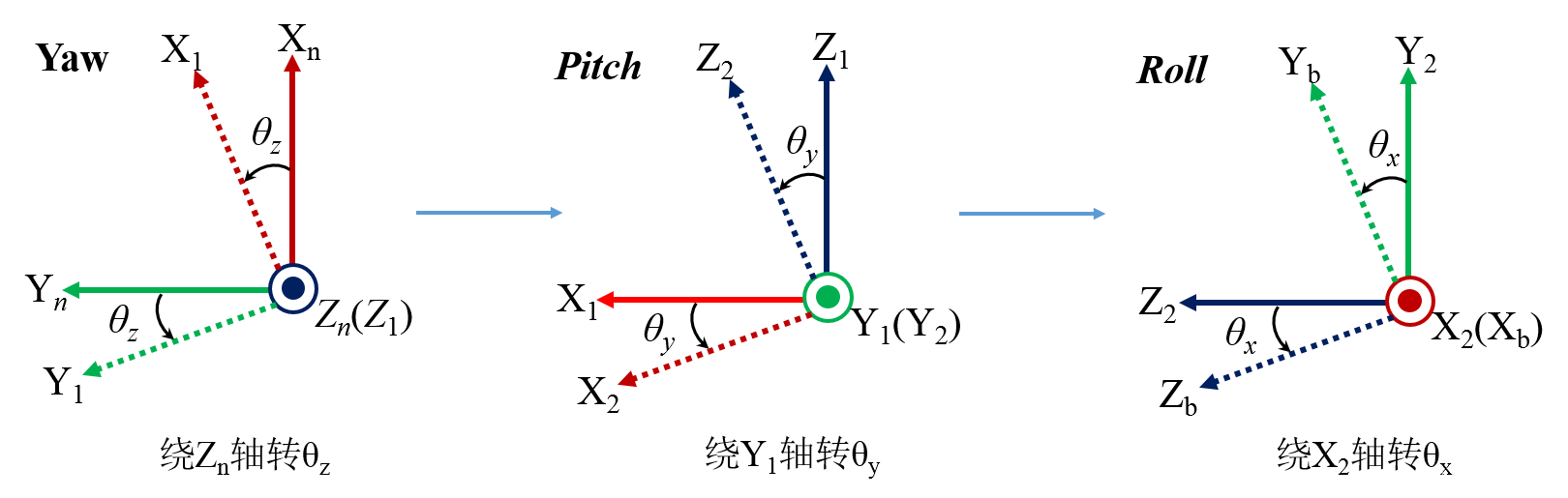
对于欧拉角计算公式我们可以得到 $\alpha ,\beta ,\gamma$ 三个角度计算得到的旋转矩阵





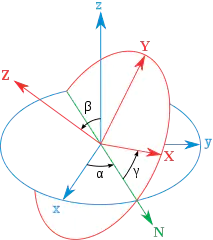
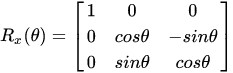
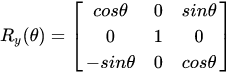
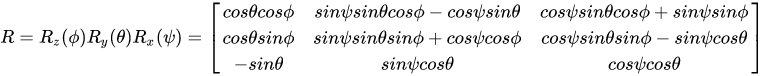
上式中$R$与旋转次序有关，即当$\theta z，\theta y，\theta x$不都为小角时，对应于不同的旋转次序，空间坐标系b的最终位置时不同的，这就是有限转动的不可交换性。但是当$\theta z，\theta y，\theta x$都为小角时，忽略小角间的高阶小量,即：$\Delta x\to 0,cos\Delta x\to 1，sin\Delta x\to \Delta x$
$R\approx \hat{n}=\left[\begin{array}{ccccc}0& & -n_z& & n_y\\ n_z& & 0& & -n_x\\ -n_y& & n_x& & 0\end{array}\right]$

其中$\theta z，\theta y，\theta x$角度为弧度，此时$\theta z，\theta y，\theta x$构成的列向量$[\theta z，\theta y，\theta x{]}^T$可视为三维空间的（旋转）矢量，此时旋转后的坐标系的最终角位置与旋转次序无关：无限转动与旋转次序无关

2. SE(2)与SE(3)的转换

SE(2)，通常是作为二维向量的表示形式，基本的组成部分为$x,y,yaw$三参数，其格式如下：

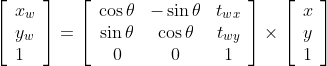
SE(3)则是在上式的基础上加入$z$轴，其格式如下：

$\left[\begin{array}{c}{x}_w\\ y_w\\ z_w\\ 1\end{array}\right]=\left[\begin{array}{ccccccc}{c}_1{c}_3+s_1{s}_2{s}_3& & c_3{s}_1{s}_2-c_1{s}_3& & c_2{s}_1& & t_{w}x\\ c_2{s}_3& & c_2{c}_3& & -s_2& & t_{w}y\\ c_1{s}_2{s}_3-s_1{c}_3& & s_1{s}_3+c_1{c}_3{s}_2& & c_1{c}_2& & t_{w}z\\ 0& & 0& & 0& & 1\end{array}\right]\times \left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$

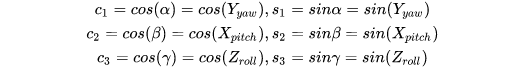
李群	SO(3)	SE(3)
旋转矩阵构建	Sophus::SO3d SO3(R)	Sophus::SE3d SE3(R,t)
四元数构建	Sophus::SO3d SO3(q)	Sophus::SO3d SO3(q,t)
输出	SO3.matrix()	SE3.matrix()
对数映射	Vector3d so3=SO3.log()	Vecotr6d se3=SE3.log()
指数映射	SO3d::exp(so3)	SE3d::exp(se3)
向量到反对称矩阵	SO3d::hat(so3)	SE3d::hat(se3)
反对称矩阵到向量	SO3d::vee(hat)	SE3d::vee(hat)

3. 示例代码

…详情请参照古月居