题目链接
好久没有写题了复健一下qwq

---

题目大意

---

解题思路

这题目还挺妙的
首先考虑比较正常的dp，$dp[i][j]$ 为前$i$的长度选$j$个长度的最大价值，那么转移方程是：
图片来自：图片来源

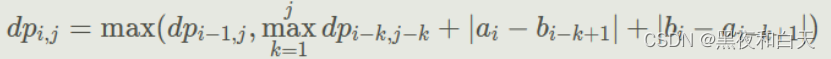
但是这个是$O(n{k}^2)$无法通过把绝对值展开进行讨论

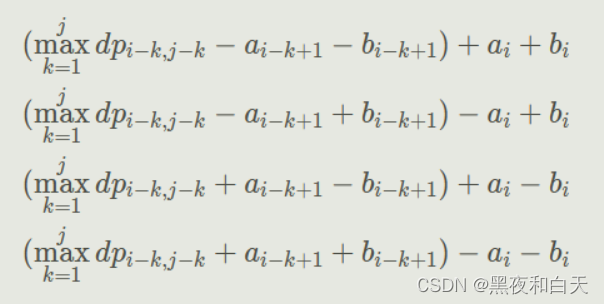
• 我们可以看到$dp[i][j]$其实都是由对角线上的$dp$值$+$几个$a$,$b$的计算，那么我们可以把前面的部分用新的数组维护起来因为都是对角上的数值那么$i-j$是固定值那么就是$f[0/1/2/3][i-j]$里面取最大值$+$后缀部分
• 然后因为这个虽然是对角线的上值的前$k$里面的最大值，但是其实$dp[i][j]>dp[i-1][j-1]$是一定成立的所以$f[0/1/2/3][i-j]$只用从$k=1$转移就行

				f[0][i - j] = std::max(f[0][i - j], dp[i - 1][j - 1] - a[i] - b[i]);f[1][i - j] = std::max(f[1][i - j], dp[i - 1][j - 1] + a[i] - b[i]);f[2][i - j] = std::max(f[2][i - j], dp[i - 1][j - 1] - a[i] + b[i]);f[3][i - j] = std::max(f[3][i - j], dp[i - 1][j - 1] + a[i] + b[i]);

• 记住f数组要初始化为负无穷，不能是0

memset(f,0x80,sizeof(f));

• 整体代码

#include <iostream>
#include <cstring>
#include <cmath>
#include <vector>
#include <algorithm>
using namespace std;
const int maxn = 3005;
typedef long long ll;
const ll mod = 998244353;
int a[maxn], b[maxn];
ll dp[maxn][maxn], f[4][maxn]; 
int main() {//freopen("1.txt","r",stdin);int T;scanf("%d",&T);while(T --) {int n, k;scanf("%d%d",&n,&k);memset(f,0x80,sizeof(f));// 这个0x80初始化出来是复数 for(int i = 1; i <= n; ++ i) cin >> a[i];for(int i = 1; i <= n; ++ i) cin >> b[i]; for(int i = 1; i <= n; ++ i) {for(int j = 1; j <= k && j <= i; ++ j) {dp[i][j] = dp[i-1][j];f[0][i - j] = std::max(f[0][i - j], dp[i - 1][j - 1] - a[i] - b[i]);f[1][i - j] = std::max(f[1][i - j], dp[i - 1][j - 1] + a[i] - b[i]);f[2][i - j] = std::max(f[2][i - j], dp[i - 1][j - 1] - a[i] + b[i]);f[3][i - j] = std::max(f[3][i - j], dp[i - 1][j - 1] + a[i] + b[i]);dp[i][j] = std::max(dp[i][j], f[0][i - j] + a[i] + b[i]);dp[i][j] = std::max(dp[i][j], f[1][i - j] + a[i] - b[i]);dp[i][j] = std::max(dp[i][j], f[2][i - j] - a[i] + b[i]);dp[i][j] = std::max(dp[i][j], f[3][i - j] - a[i] - b[i]);
//                for(int h = 1; h <= j; ++ h) {
//                    dp[i][j] = max(dp[i-h][j-h]+abs(a[i]-b[i-h+1])+abs(a[i-h+1]-b[i]),dp[i][j]);
//                    // printf("%d %d %lld\n",i,j,dp[i][j]);
//                }}}printf("%lld\n",dp[n][k]);} return 0;
}

• 上面你可能会疑问这个不是抵消了吗？

f[0][i - j] = std::max(f[0][i - j], dp[i - 1][j - 1] - a[i] - b[i]);
dp[i][j] = std::max(dp[i][j], f[0][i - j] + a[i] + b[i]);

注意其实这里的有个影响是$f[0][i-j]$是包含了带$k$的参数 所以要做两次$max$,$dp[i-1][j-1]-a[i]-b[i]$只是刚好这一层儿而已