一.Bagging与Boosting的区别
在上一章里我们学习了一个集成模型叫作随机森林,而且也了解到随机森林属于Bagging的成员。本节我们重点来学习一下另外一种集成模型叫作Boosting。首先回顾一下什么叫Bagging? 比如在随机森林里,针对于样本数据,我们同时训练了多棵决策树,然后让这些决策树通过投票的方式来参与预测。这种方式的好处也讲过,可以很好地提升模型的稳定性。 其实任意的集成模型只要训练得合理都具备这种特性的,Boosting也不例外。
首先,在Bagging和Boosting里,我们把每一个模型称作Weak Learner,比如随机森林里的每一棵决策树就是Weak Leaner。那怎么理解Weak Learner呢? 其实就是不太靠谱的模型,但很多不太靠谱的模型组合在一起最终得出来的很可能是靠谱的模型,是不是很神奇?
虽然Bagging和Boosting都由Weak Learner来组成,但它们之间还是有很大区别的。有两个关键词我们还需要记住:overfitting和underfitting。 前者的意思是一个模型训练得太好了、太厉害了,导致出现过拟合的现象,所以不靠谱; 后者的意思是这么模型有点弱,都没有充分训练过,所以不靠谱。Bagging是很多过拟合的Weak Leaner来组成,Boosting是很多欠拟合的Weak Learner来组成,这就是它们之间核心的区别。
可以举个例子:Bagging模型可以理解成由很多顶级的专家来组成,但这些专家呢,都自以为很厉害都听不进去别人的意见,所以遇到新的问题适应能力稍微弱一些。但是呢,让这些专家通过合作一起做事情的时候就非常厉害。另外一方面,Boosting模型可以理解成由很多学渣来组成,每一个人的能力都挺弱的,而且不能够独当一面。但是呢,当很多人一起合作的时候却能带来惊人的结果。
二.提升树--基于残差的训练
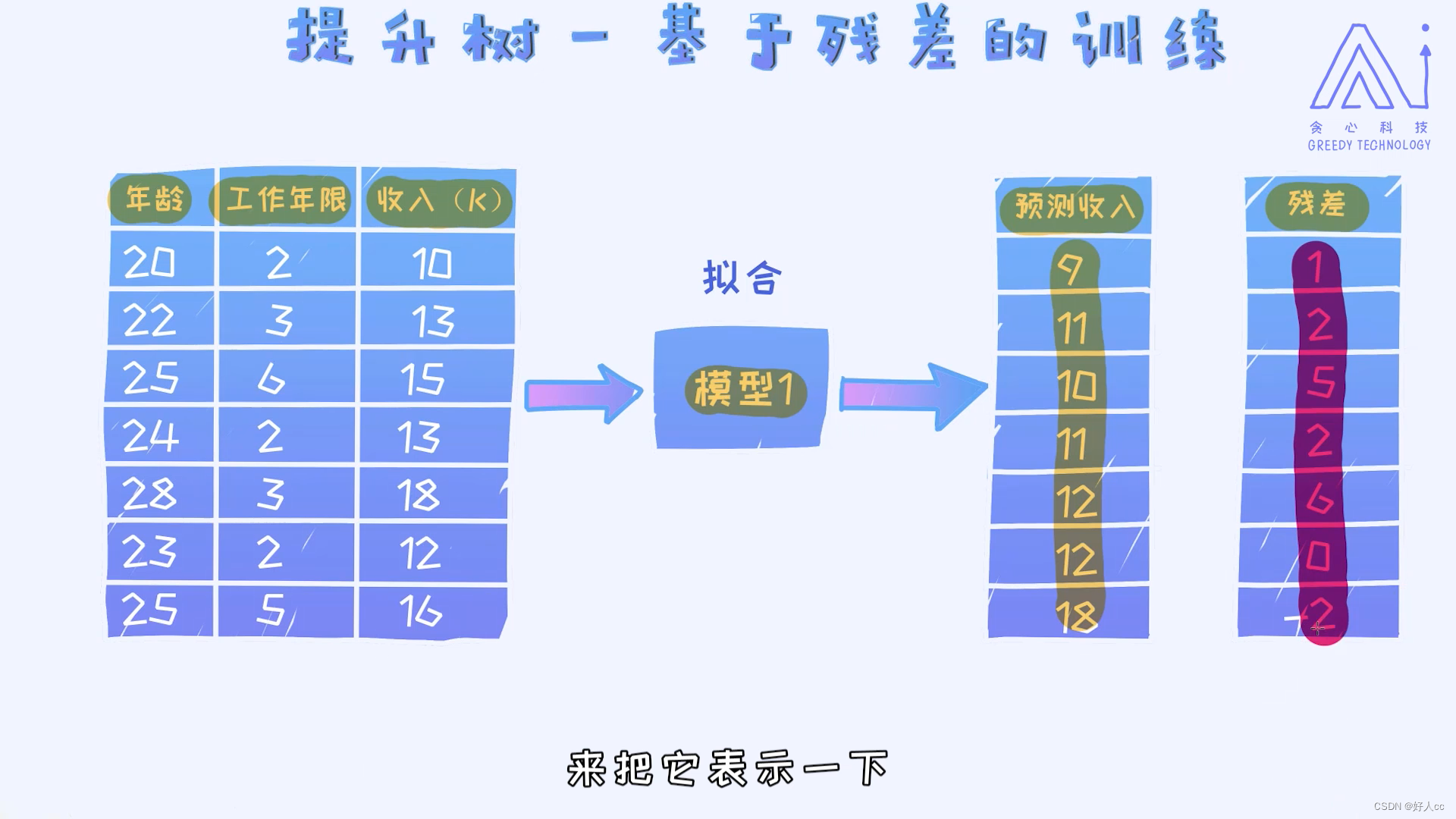
用残差代替收入,以此类推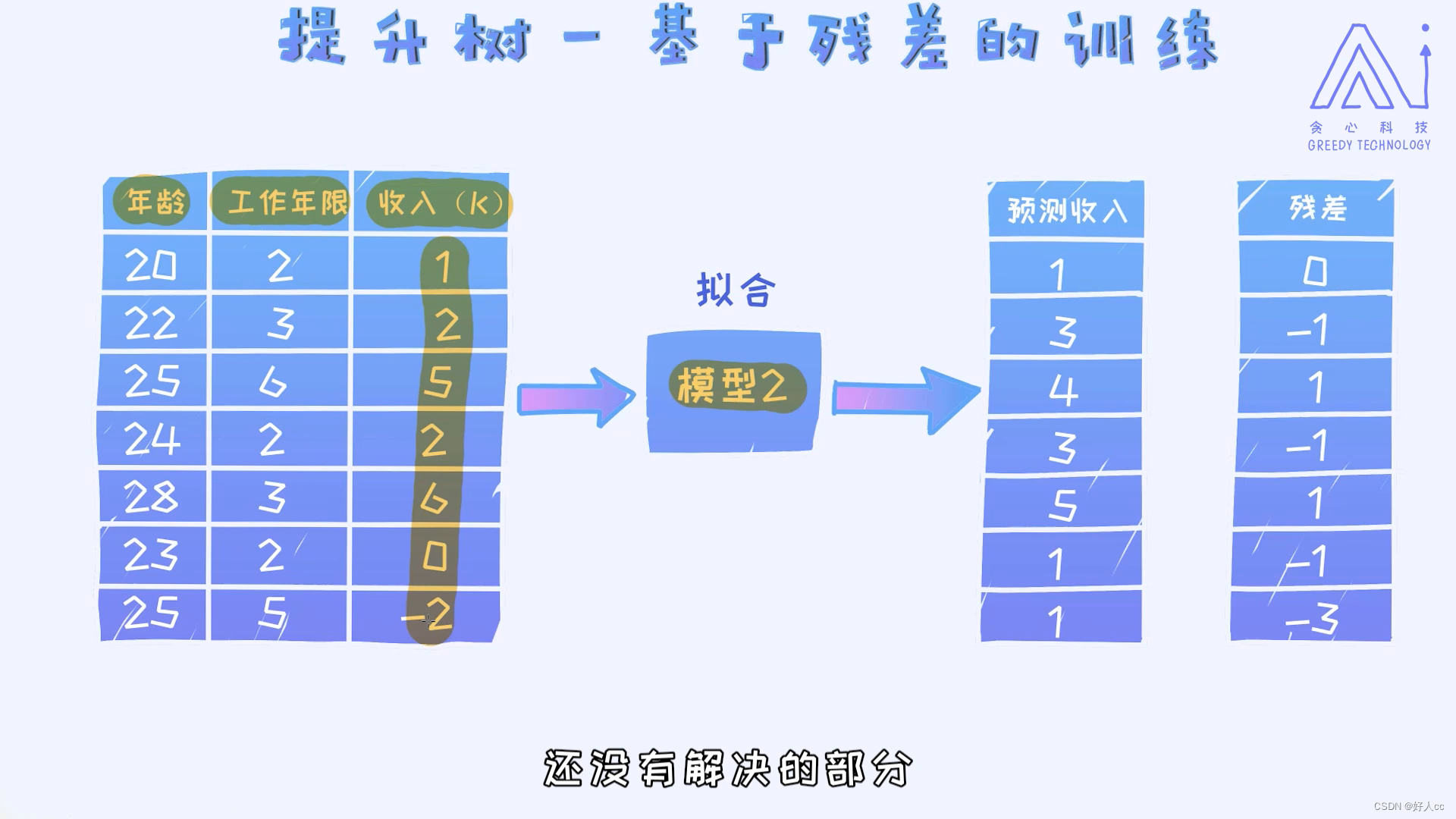
问题:对于回归问题,假如我们按照残差的方式学习了很多棵决策树,决策的时候怎么办?
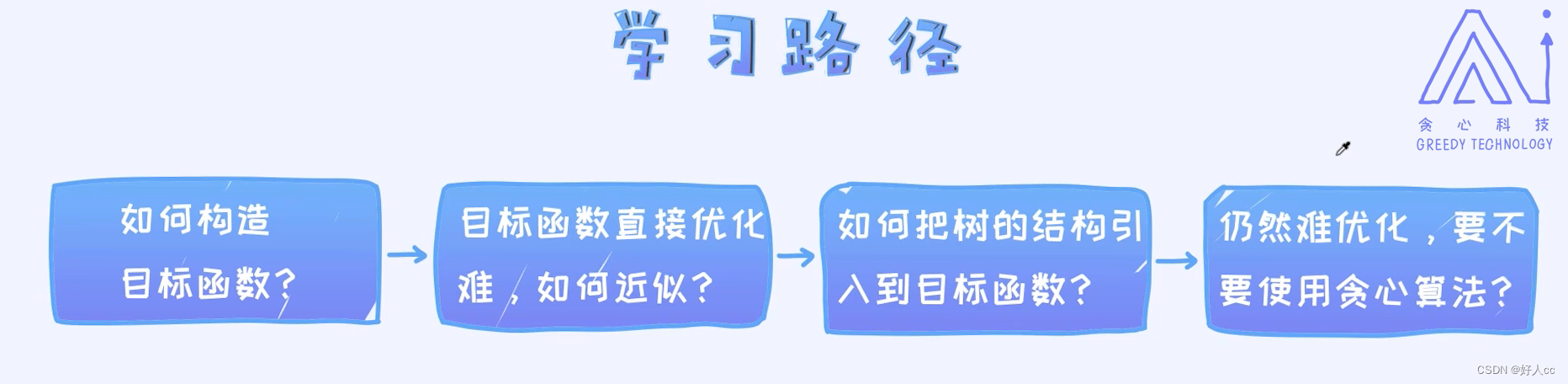
 三.XGBoost
三.XGBoost

那XGBoost如何学习呢? 最好的资源无非是Tianqi自己写的PPT,链接请参考:https://homes.cs.washington.edu/~tqchen/pdf/BoostedTree.pdf
四.XGBoost目标函数
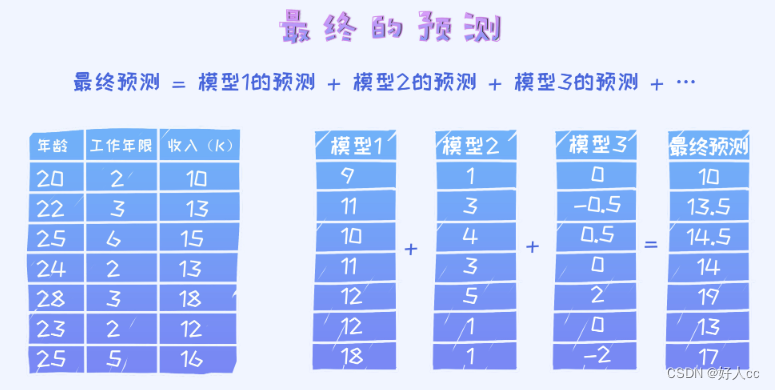
当拿到一个样本之后,分别通过每一个模型做预测,最后每个模型输出之和作为最终的预测结果。我们可以把这个过程泛化到具有K棵树的情况。
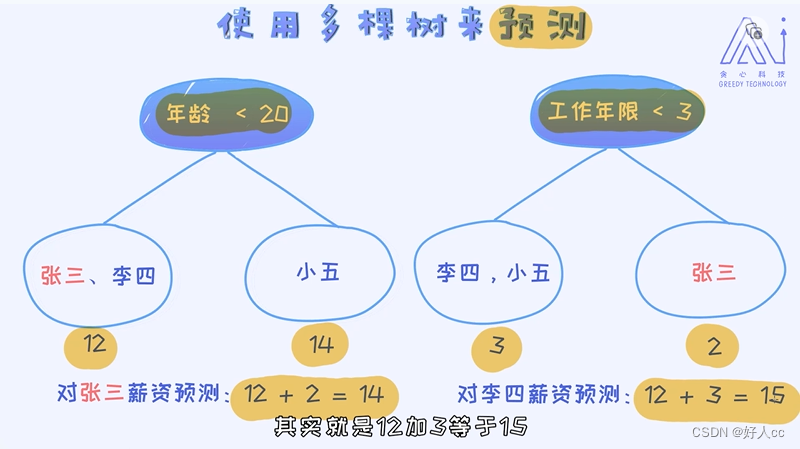 最后的结果相当于所有K棵树预测之和。这里的fk(xi)代表第k棵树对第i个样本的预测值。简单来讲,这里的函数f可以看作是每一棵训练好的决策树。
最后的结果相当于所有K棵树预测之和。这里的fk(xi)代表第k棵树对第i个样本的预测值。简单来讲,这里的函数f可以看作是每一棵训练好的决策树。
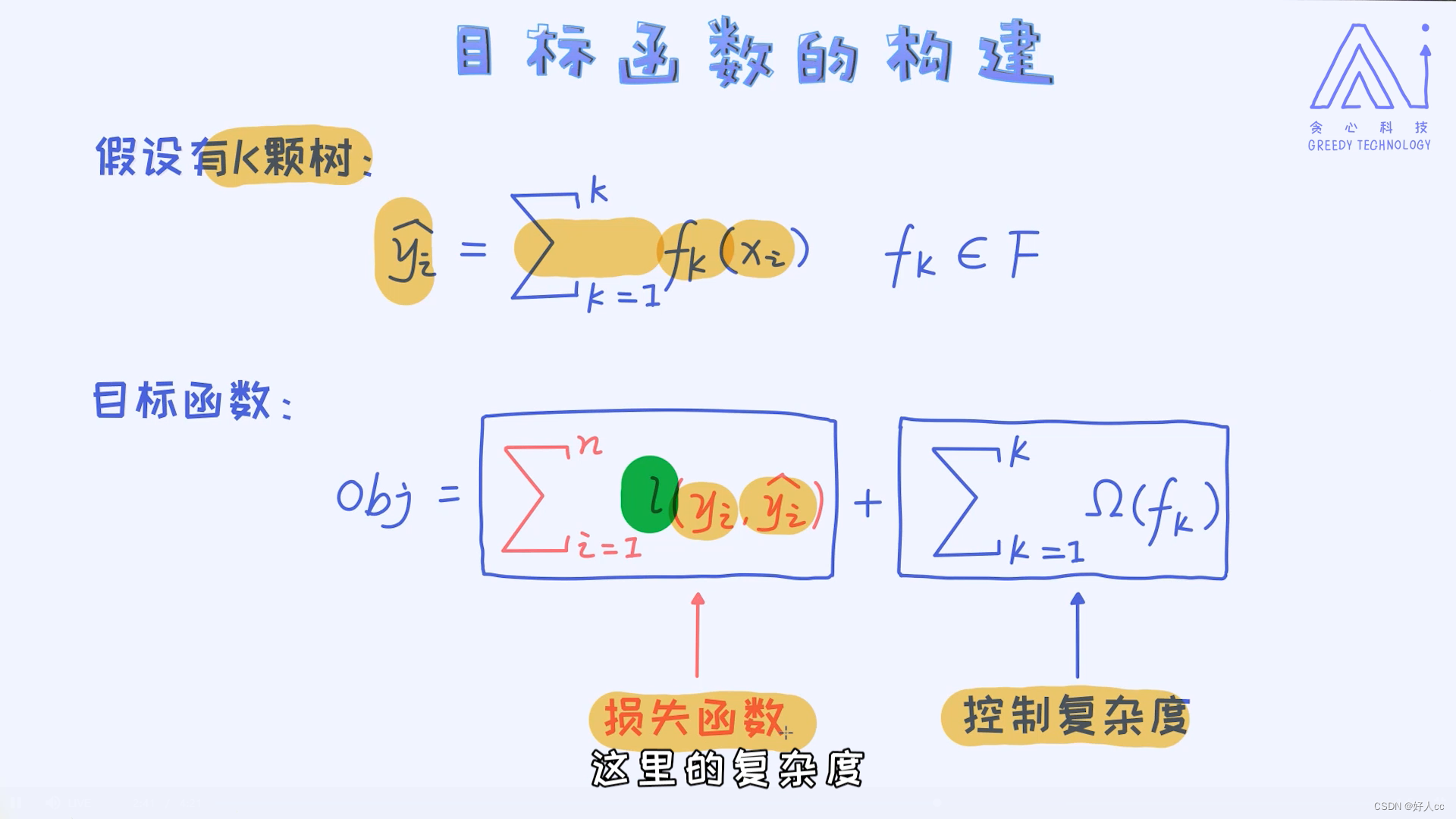
这里的目标函数由两个部分来构成,其中一项是损失函数,另外一项是控制模型的复杂度项。如果是回归问题,我们可以使用最小二乘作为损失函数;如果是分类问题,我们则可以使用交叉熵作为损失函数;这里的函数l(。,。)表示预测值与真实值之间的差异。所以,从这里也可以看出XGBoost既可以用在回归问题上,也可以用在分类问题上,因为框架本身是通用的。
除了损失函数,我们在使用模型的时候一般也会加入控制复杂度的项,也叫作正则。 回顾一下,在线性回归或者逻辑回归上我们考虑过L1、L2这些常用的正则。正则的作用无非就是控制模型的复杂度,从而把容易过拟合的模型不给予考虑。那这里问题是:我们该如何给XGBoost模型定义复杂度?这个问题的本质其实:一棵决策树的复杂度如何定义? 或者换个角度:一棵复杂的决策树模型有什么特点?
五.新的目标函数

剩下的事情就最小化新的目标函数了。 这个过程其实等同于寻找一棵最好的树,使得让这个目标函数最小。那这棵树如何寻找呢? 这其实就是优化问题了!

做差越大,越好。
这就是我们想要的答案! 其实训练过程跟决策树非常类似,无非是每次考虑的评估方式不一样。在决策树里,每次考虑的是信息增益或者方差的增益,只不过在xgboost的构建当中我们每次考虑的是自定义的目标函数的差异罢了。所以从整个过程也可以看得到,虽然一开始一步步试图构建参数化的目标函数,但最后还是回到了基于贪心算法的树的构建,跟决策树的构建很类似。只不过我们在构建决策树时并没有试图去创建什么目标函数,而是直接通过信息增益来搭建,所以直接看到的是结果,省略了中间很多步骤而已。以上是所有核心的算法细节,具体系统上的优化细节建议翻翻论文里的内容。XGBoost很好用,具体API可以参考:XGBoost Documentation — xgboost 2.1.0-dev documentation



