数据结构-----堆(完全二叉树)

news/2024/12/22 13:30:01/

 目录

前言

一.堆

1.堆的概念

2.堆的存储方式

二.堆的操作方法

1.堆的结构体表示

2.数字交换接口函数

3.向上调整（难点）

4.向下调整（难点）

5.创建堆

 6.堆的插入

 7.判断空

8.堆的删除

 9.获取堆的根(顶)元素

10.堆的遍历

 11.销毁堆

完整代码

三.堆的应用（堆排序）

1.算法介绍

2.基本思想

3.代码实现

4.算法分析

前言

         今天我们开始学习一种二叉树，没错，那就是完全二叉树，完全二叉树又叫做堆，在此之前我们简单介绍过了完全二叉树的概念（链接：数据结构-----树和二叉树的定义与性质_灰勒塔德的博客-CSDN博客），这种类型的二叉树又有什么特点呢？代码怎么去实现呢？应用有那些呢？下面就一起来看看吧！

一.堆

1.堆的概念

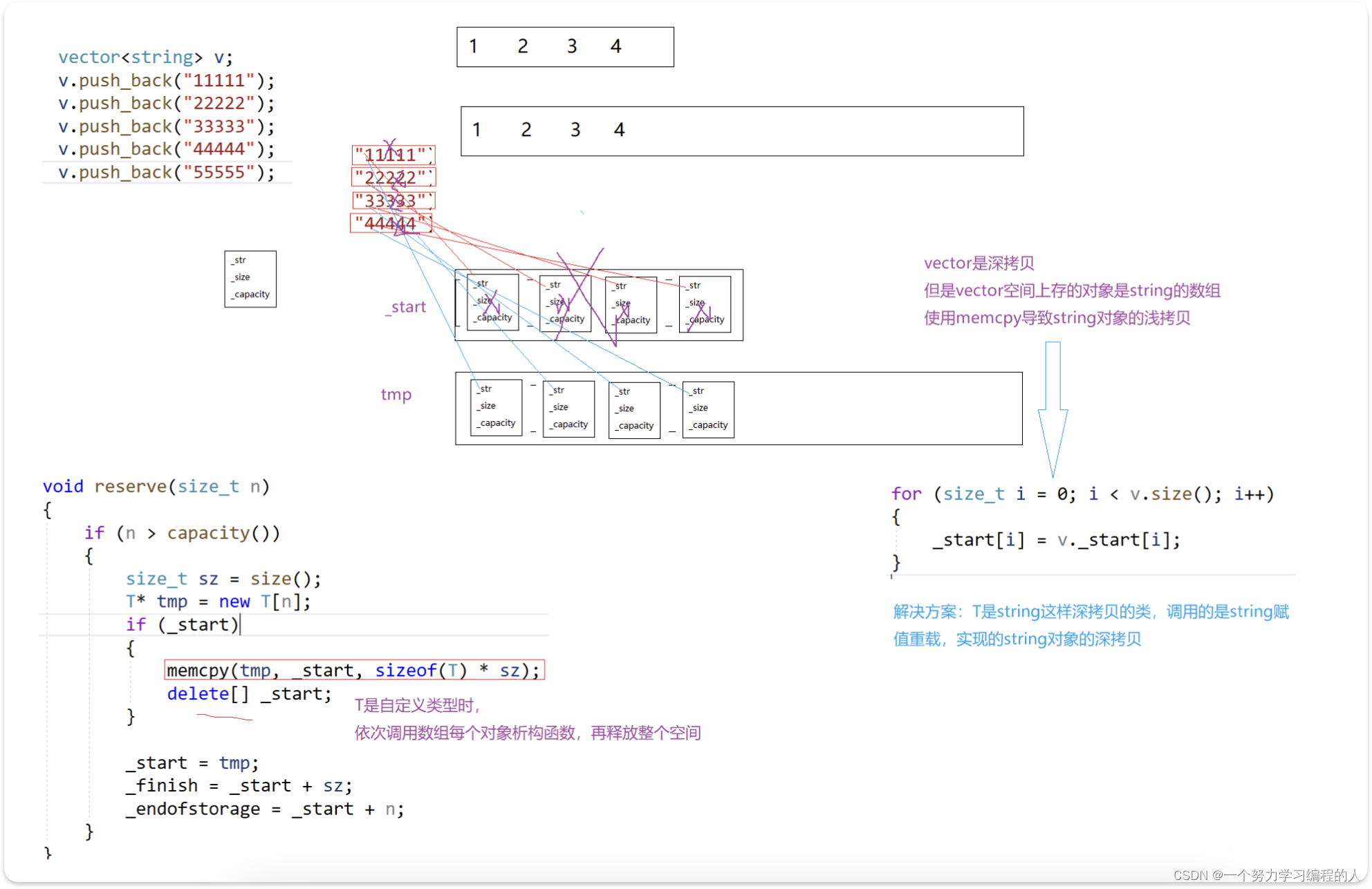
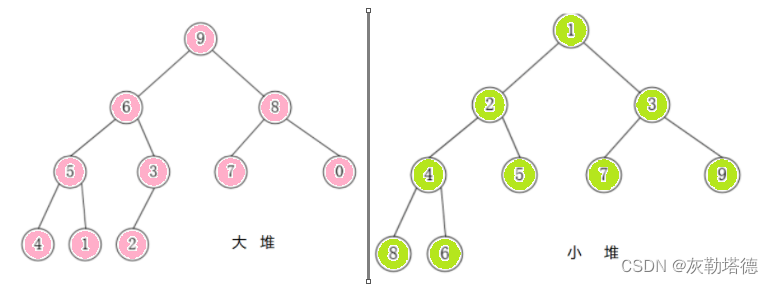
堆（heap）是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象，物理层面上是一个数组，逻辑上是一个完全二叉树。堆总是满足下列性质：

  • 堆中某个结点的值总是不大于或不小于其父结点的值；

  • 堆总是一棵完全二叉树。

  • 满足任意父节点都大于子节点的称作为大堆

  • 满足任意子节点都大于父节点的称作为小堆

  • tip:（下文会以大堆的创建为示例）

如图所示：

 

2.堆的存储方式

堆的储存原则是从上到下，从左到右，也就是说先有上面的父节点才会有子节点，先有左子节点，才会有右子节点 ，所以堆可以去通过一个数组完整的表示出来，如下图所示：

二.堆的操作方法

以下是一个堆要实现的基本功能，下面我会一一去详细解释说明

void swap(DataType* a, DataType* b);//交换数据void Adjust_Up(DataType* data, int child, int n);//向上调整void Adjust_Down(DataType* data, int parent, int n);//向下调整void Heap_Create(Heap* hp, DataType* data, int n);//创建堆bool isEmpty(Heap* hp);//判断空void Heap_Insert(Heap* hp, DataType x);//堆的插入void Heap_Del(Heap* hp);//堆的删除操作DataType Heap_Root(Heap* hp);//获取根元素void Heap_show(Heap* hp);//堆的遍历void Heap_Destory(Heap* hp);//堆的销毁

1.堆的结构体表示

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#define Maxsize 50//顺序结构
//堆（完全二叉树）
typedef int DataType;	//定义数据的类型
typedef struct Heap
{int size;	//当前节点数量int capacity;	//最大容量DataType* data;	//数据储存地址
}Heap;

2.数字交换接口函数

//数据交换接口
void swap(DataType* a, DataType* b) {DataType temp = *a;*a = *b;*b = temp;
}

3.向上调整（难点）

        创建大堆时，向上调整的目的是，在有子节点位置的情况下，进行与父节点的大小比较，如果子节点大于父节点，那么就进行交换，然后新的子节点就是上一个的父节点，依次这样比较下去，最后到根节点为止，如图所示：

 代码实现：

//向上调整
void Adjust_Up(DataType* data, int child, int n) {int parent = (child - 1) / 2;while (child > 0) {//如果子节点大于父节点就进行数值交换，然后此时的子节点就是前一个父节点，再找到//新的父节点，继续进行同样的操作，直到根节点为止if (data[child] > data[parent]){swap(&data[child], &data[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}

4.向下调整（难点）

        同样的还有向下调整，如果有了当前的父节点位置，那么就要跟子节点进行比较，但是子节点有左和右子节点，所以左右子节点也要去比较，取到其中比较大的子节点与父节点比较，如果这个字节点大于父节点的话，那就进行数字交换，然后新的父节点就是上一个的子节点，依次往下遍历进行同样的操作。

代码实现： 

//向下调整
void Adjust_Down(DataType* data, int parent, int n) {int child = parent * 2 + 1;while (child <n ) {if (child+1 < n && data[child] < data[child+1]){//如果右子节点大于左子节点，那就child+1，选中到右子节点child++;}if (data[child] > data[parent]) {//同样的，有了当前父节点，然后找到子节点，进行向下遍历调整操作swap(&data[child], &data[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}

5.创建堆

已有一个数组{ 5,1,2,3,6,4,8 }，怎么把这个数组放入堆里面呢？同样的，空间申请去申请到一块连续的空间，然后依次把数据存入到这个数组里面去，最后进行向下调整，以达到堆的形式。

放入堆之后如下图所示： 

代码实现：

//创建堆
void Heap_Create(Heap* hp, DataType* data, int n) {assert(hp);hp->data = (DataType*)malloc(sizeof(DataType) * n);if (!hp->data) {printf("ERROR\n");exit(-1);}for (int i = 0; i < n; i++) {hp->data[i] = data[i];//赋值}hp->size = n;hp->capacity = Maxsize;for (int j = (n - 1) / 2; j >= 0; j--) {//创建完成了之后，就要进行向下调整Adjust_Down(hp->data, j ,hp->size);}
}

 6.堆的插入

堆的插入，就是在堆的最后面去添加一个元素，添加完成之后，就要去进行向上调整操作，如下图所示：

代码实现： 

//堆的插入
void Heap_Insert(Heap* hp, DataType x) {assert(hp);//如果此时的堆空间满了，那么就要去扩容空间if (hp->size == hp->capacity) {DataType* temp = (DataType*)realloc(hp->data,sizeof(DataType)  * (hp->capacity+1));//追加1个空间if (!temp) {printf("ERROR\n");exit(-1);}hp->data = temp;hp->data[hp->size] = x;hp->size++;hp->capacity++;}else{hp->data[hp->size] = x;hp->size++;}Adjust_Up(hp->data, hp->size - 1, hp->size);//插入后进行向上调整
}

 7.判断空

//判断空
bool isEmpty(Heap* hp) {assert(hp);return hp->size == 0;
}

8.堆的删除

堆的删除操作是删除掉根节点，过程是，先把最后一个节点与根节点进行交换，然后重新进行向下调整。（堆的删除操作，删除掉的是根节点！）

代码实现： 

//堆的删除,删除根节点
void Heap_Del(Heap* hp) {assert(hp);if (!isEmpty(hp)) {swap(&hp->data[hp->size - 1], &hp->data[0]);//根节点和尾节点进行交换hp->size--;Adjust_Down(hp->data, 0, hp->size);//向下调整}
}

 9.获取堆的根(顶)元素

//获取堆顶元素
DataType Heap_Root(Heap* hp) {assert(hp);if (!isEmpty(hp))return hp->data[0];elseexit(0);
}

10.堆的遍历

堆的遍历就直接按照数组的顺序去遍历就行了，完全二叉树的逻辑上是从上到下，从左到右去遍历的，代码如下：

//输出堆元素（按照顺序）
void Heap_show(Heap* hp) {assert(hp);if (isEmpty(hp)) {printf("The Heap is etmpy\n");return;}for (int i = 0; i < hp->size; i++)printf("%d ", hp->data[i]);
}

 11.销毁堆

//堆的销毁
void Heap_Destory(Heap* hp) {assert(hp);hp->size = hp->capacity = 0;free(hp);//释放空间
}

完整代码

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#define Maxsize 50//顺序结构
//堆（完全二叉树）
typedef int DataType;	//定义数据的类型
typedef struct Heap
{int size;	//当前节点数量int capacity;	//最大容量DataType* data;	//数据储存地址
}Heap;//数据交换接口
void swap(DataType* a, DataType* b) {DataType temp = *a;*a = *b;*b = temp;
}//向上调整
void Adjust_Up(DataType* data, int child, int n) {int parent = (child - 1) / 2;while (child > 0) {//如果子节点大于父节点就进行数值交换，然后此时的子节点就是前一个父节点，再找到//新的父节点，继续进行同样的操作，直到根节点为止if (data[child] > data[parent]){swap(&data[child], &data[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}//向下调整
void Adjust_Down(DataType* data, int parent, int n) {int child = parent * 2 + 1;while (child <n ) {if (child+1 < n && data[child] < data[child+1]){//如果右子节点大于左子节点，那就child+1，选中到右子节点child++;}if (data[child] > data[parent]) {//同样的，有了当前父节点，然后找到子节点，进行向下遍历调整操作swap(&data[child], &data[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//创建堆
void Heap_Create(Heap* hp, DataType* data, int n) {assert(hp);hp->data = (DataType*)malloc(sizeof(DataType) * n);if (!hp->data) {printf("ERROR\n");exit(-1);}for (int i = 0; i < n; i++) {hp->data[i] = data[i];//赋值}hp->size = n;hp->capacity = Maxsize;for (int j = (n - 1) / 2; j >= 0; j--) {//创建完成了之后，就要进行向下调整Adjust_Down(hp->data, j ,hp->size);}
}//判断空
bool isEmpty(Heap* hp) {assert(hp);return hp->size == 0;
}//堆的插入
void Heap_Insert(Heap* hp, DataType x) {assert(hp);//如果此时的堆空间满了，那么就要去扩容空间if (hp->size == hp->capacity) {DataType* temp = (DataType*)realloc(hp->data,sizeof(DataType)  * (hp->capacity+1));//追加1个空间if (!temp) {printf("ERROR\n");exit(-1);}hp->data = temp;hp->data[hp->size] = x;hp->size++;hp->capacity++;}else{hp->data[hp->size] = x;hp->size++;}Adjust_Up(hp->data, hp->size - 1, hp->size);//插入后进行向上调整
}//堆的删除,取出根节点
void Heap_Del(Heap* hp) {assert(hp);if (!isEmpty(hp)) {swap(&hp->data[hp->size - 1], &hp->data[0]);//根节点和尾节点进行交换hp->size--;Adjust_Down(hp->data, 0, hp->size);//向下调整}
}//获取堆顶元素
DataType Heap_Root(Heap* hp) {assert(hp);if (!isEmpty(hp))return hp->data[0];elseexit(0);
}//输出堆元素（按照顺序）
void Heap_show(Heap* hp) {assert(hp);if (isEmpty(hp)) {printf("The Heap is etmpy\n");return;}for (int i = 0; i < hp->size; i++)printf("%d ", hp->data[i]);
}//堆的销毁
void Heap_Destory(Heap* hp) {assert(hp);hp->size = hp->capacity = 0;free(hp);//释放空间
}

三.堆的应用（堆排序）

1.算法介绍

        堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

2.基本思想

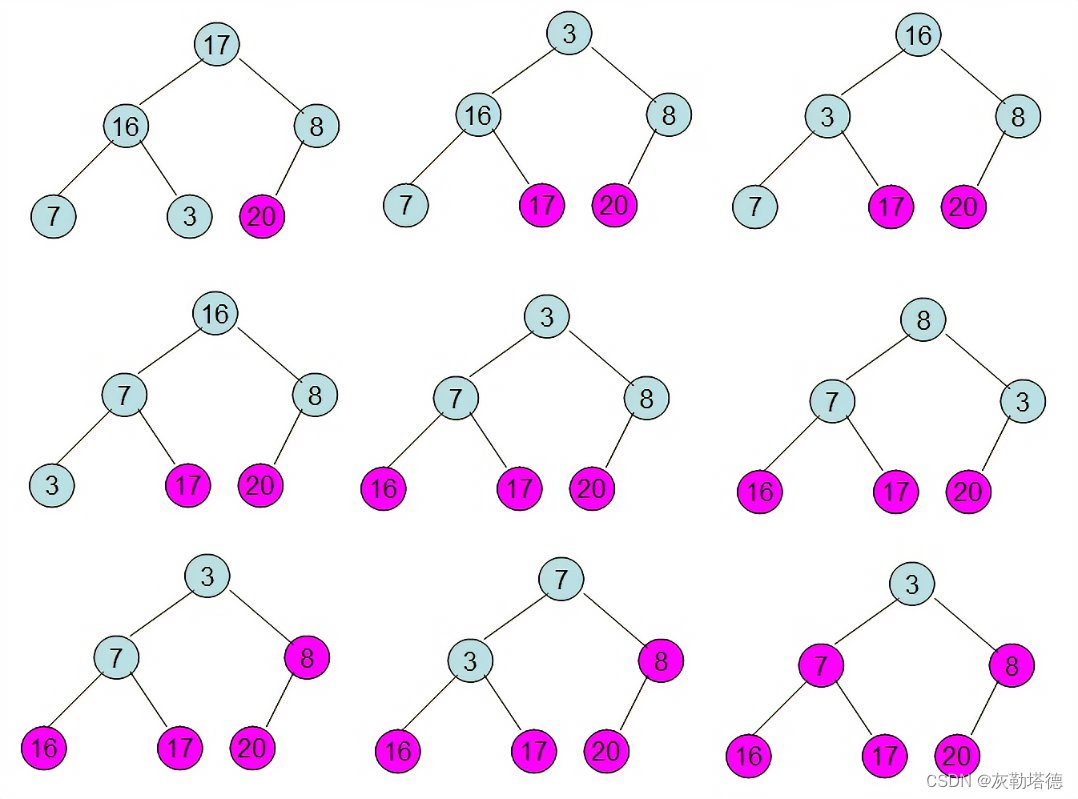
利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性，使得每次从无序中选择最大记录(最小记录)变得简单。

① 将待排序的序列构造成一个最大堆，此时序列的最大值为根节点
② 依次将根节点与待排序序列的最后一个元素交换
③ 再维护从根节点到该元素的前一个节点为最大堆，如此往复，最终得到一个递增序列

3.代码实现

#include<stdio.h>
#include<assert.h>
//数据交换接口
void swap(int *a, int *b) {int temp = *a;*a = *b;*b = temp;
}//向下调整
void Adjust_Down(int* data, int parent, int n) {int child = parent * 2 + 1;while (child < n) {if (child + 1 < n && data[child] < data[child + 1]){//如果右子节点大于左子节点，那就child+1，选中到右子节点child++;}if (data[child] > data[parent]) {//同样的，有了当前父节点，然后找到子节点，进行向下遍历调整操作swap(&data[child], &data[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//堆排序算法
void Heap_sort(int* arr, int n) {assert(arr);for (int i = (n - 2) / 2; i >= 0; i--) {Adjust_Down(arr, i, n);}//先形成最大堆int end = n - 1;//从小到大排序while (end > 0) {swap(&arr[0], &arr[end]);Adjust_Down(arr, 0, end);end--;	//此时最后一个也就是当前的最大值已经排序好了}
}int main() {int a[9] = { 5,1,2,3,6,4,8,2,10 };Heap_sort(a, sizeof(a) / sizeof(int));for (int i = 0; i < sizeof(a) / sizeof(int); i++) {printf("%d ", a[i]);}
}
//输出
//1 2 2 3 4 5 6 8 10

4.算法分析

  • 平均时间复杂度：O(nlogn)
  • 最佳时间复杂度：O(nlogn)
  • 最差时间复杂度：O(nlogn)
  • 稳定性：不稳定

 以上就是本期的内容，我们下次见！

 分享一张壁纸：


http://www.ppmy.cn/news/1122738.html

相关文章

【STL】vector常见用法及模拟实现(附源码）

【STL】vector常见用法及模拟实现(附源码）

目录 前言1. vector介绍及使用1.1vector的介绍1.2 vector的使用1.2.1 构造函数 1.2.2 vector对象遍历1.2.3 reserve和resize1.2.4 insert和erase 2. vector模拟实现2.1 vector迭代器失效问题2.2 模拟实现reserve函数浅拷贝问题2.3模拟实现源码2.3.1 vector.h2.3.2 test.cpp 前言…
阅读更多...
Kafka的消息传递保证和一致性

Kafka的消息传递保证和一致性

前言 通过前面的文章&#xff0c;相信大家对Kafka有了一定的了解了&#xff0c;那接下来问题就来了&#xff0c;Kafka既然作为一个分布式的消息队列系统&#xff0c;那它会不会出现消息丢失或者重复消费的情况呢&#xff1f;今天咱们就来一探。 实现机制 Kafka采用了一系列机…
阅读更多...
华为云云耀云服务器L实例评测｜轻量级应用服务器对决：基于 fio 深度测评华为云云耀云服务器L实例的磁盘性能

华为云云耀云服务器L实例评测｜轻量级应用服务器对决：基于 fio 深度测评华为云云耀云服务器L实例的磁盘性能

本文收录在专栏&#xff1a;#云计算入门与实践 - 华为云 专栏中&#xff0c;本系列博文还在更新中 相关华为云云耀云服务器L实例评测文章列表如下&#xff1a; 华为云云耀云服务器L实例评测 | 从零开始&#xff1a;云耀云服务器L实例的全面使用解析指南华为云云耀云服务器L实…
阅读更多...
ImportError: Java package ‘edu‘ not found, requested by alias ‘edu‘

ImportError: Java package ‘edu‘ not found, requested by alias ‘edu‘

参考issue&#xff1a; https://github.com/ncbi-nlp/NegBio/issues/44 我目前的解决办法 pip uninstall jpype1 -y可以成功运行。
阅读更多...
更新GitLab上的项目

更新GitLab上的项目

更新GitLab上的项目 如有需要&#xff0c;请参考这篇&#xff1a;上传项目到gitlab上 1.打开终端&#xff0c;进入到本地项目的根目录。 2.如果你还没有将远程GitLab仓库添加到本地项目&#xff0c;你可以使用以下命令&#xff1a; 比如&#xff1a; git remote add origin …
阅读更多...
flutter web 优化和flutter_admin_template

flutter web 优化和flutter_admin_template

文章目录 Flutter Admin TemplateLive demo: https://githubityu.github.io/live_flutter_adminWeb 优化 Setup登录注册英文 亮色主题 中文 暗黑主题管理员登录权限 根据权限动态添加路由 第三方依赖License最后参考学习 Flutter Admin Template Responsive web with light/da…
阅读更多...
C语言while循环嵌套-动态字母

C语言while循环嵌套-动态字母

1、题目 使用C语言实现对字母动态移动&#xff08;根据用户输入的字符将字符从屏幕的坐标移动屏幕的右边&#xff09;。 2、分析 字符的移动核心是在显示的字母前面补上对应的空格字符内容&#xff0c;配合上延时就可以实现字符从屏幕左边移动到屏幕右侧的效果&#xff0c;实现…
阅读更多...
nginx 配置 ssl

nginx 配置 ssl

1.1 Nginx如果未开启SSL模块&#xff0c;配置Https时提示错误 原因也很简单&#xff0c;nginx缺少http_ssl_module模块&#xff0c;编译安装的时候带上--with-http_ssl_module配置就行了&#xff0c;但是现在的情况是我的nginx已经安装过了&#xff0c;怎么添加模块&#xff0…
阅读更多...
最新文章

Copyright @ 2022~2023