数据结构
- 1 栈
- 2 队列
- 3 数组
- 4 链表
- 5 二叉树
- 5.1 二叉树
- 5.2 二叉查找树
- 5.3 平衡二叉树
- 5.4 红黑树
- 6 哈希表
数据结构是计算机存储、组织数据的方式。是指相互之间存在一种或多种特定关系的数据元素的集合。
通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。
1 栈
栈是一种数据先进后出的模型
数据进入栈模型的过程称为:压/进栈
数据离开栈模型的过程称为:弹/出栈
2 队列
队列是一种数据先进先出的模型
数据从后端进入队列模型的过程称为:入队列
数据从前端离开队列模型的过程称为:出队列
3 数组
数组是一种查询快,增删慢的模型
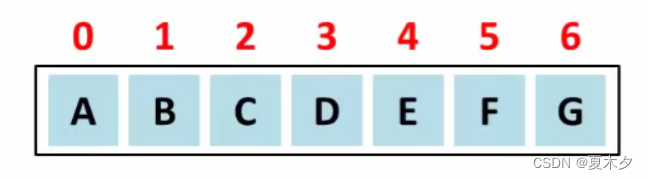
查询数据时,通过地址值和索引定位,查询任意数据耗时相同,查询速度快
删除数据时,要将原始数据删除,同时后面每个数据前移,删除效率低
添加数据时,添加位置后的每个数据后移,再添加元素,添加效率极低
4 链表
链表是一种增删快,查询慢的模型
链表中的每一个元素称之为结点,如下图:
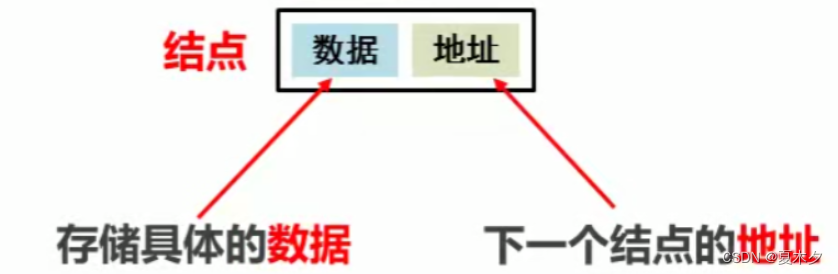
链表中第一个结点是头结点
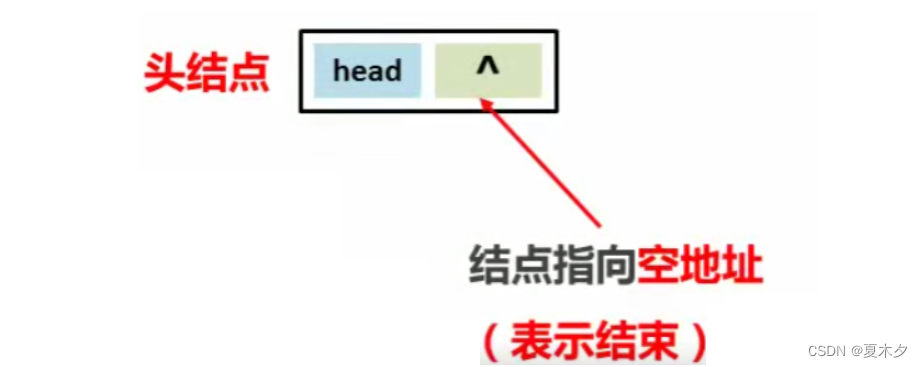 链表又可以分为:
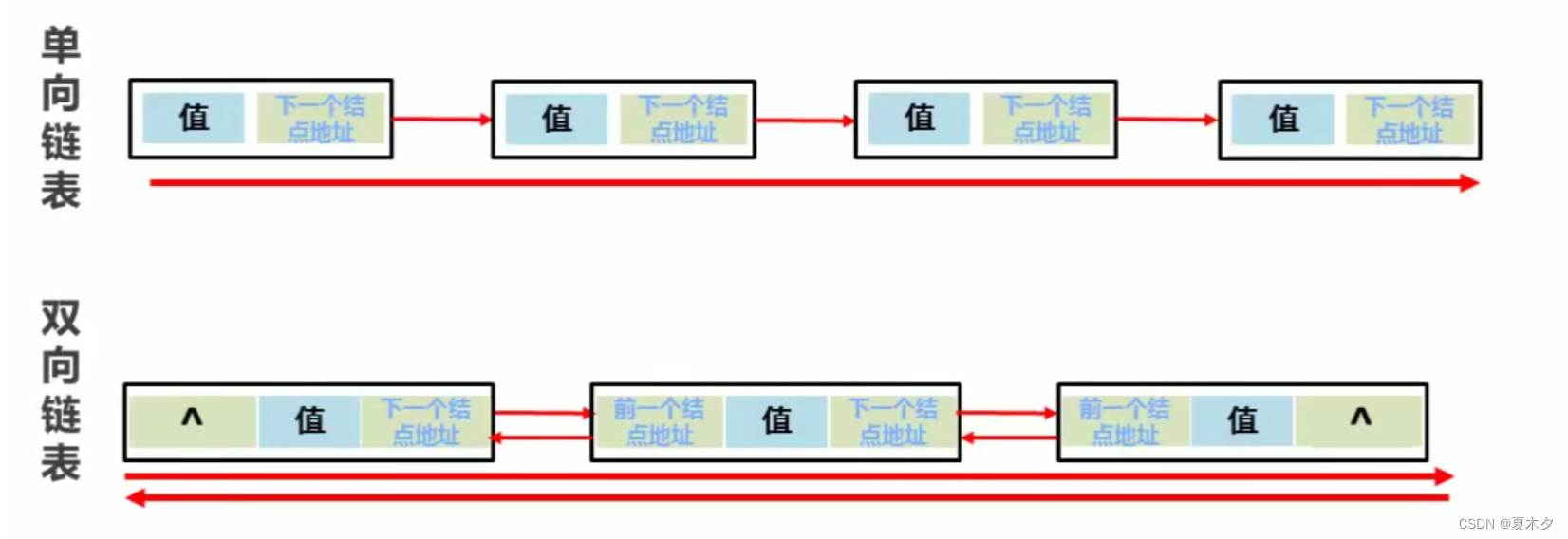
链表又可以分为:
- 单向链表
- 只能从前往后查找
- 双向链表
- 双向查找,离哪个近从哪个方向找
5 二叉树
5.1 二叉树
- 二叉树的特点:
- 二叉树中,任意一个节点的度要小于等于2
- 节点: 在树结构中,每一个元素称之为节点
- 度: 每一个节点的子节点数量称之为度
- 二叉树结构图:
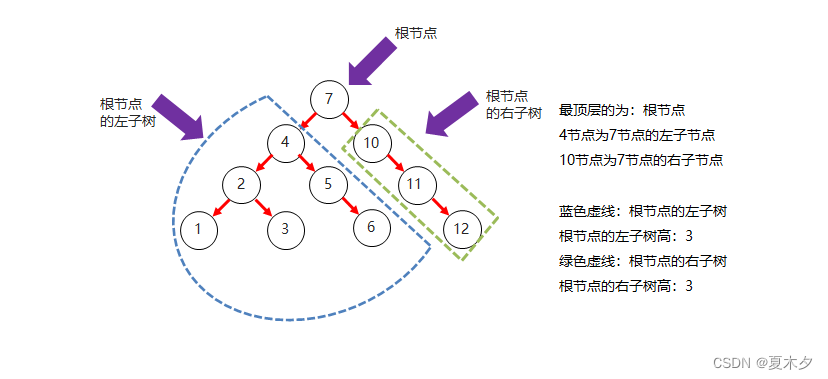
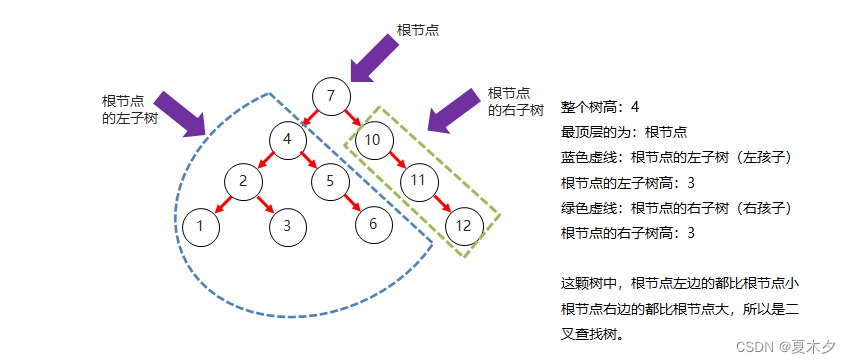
5.2 二叉查找树
- 二叉查找树的特点:
- 二叉查找树,又称二叉排序树或者二叉搜索树
- 每一个节点上最多有两个子节点
- 左子树上所有节点的值都小于根节点的值
- 右子树上所有节点的值都大于根节点的值
- 二叉查找树结构图:
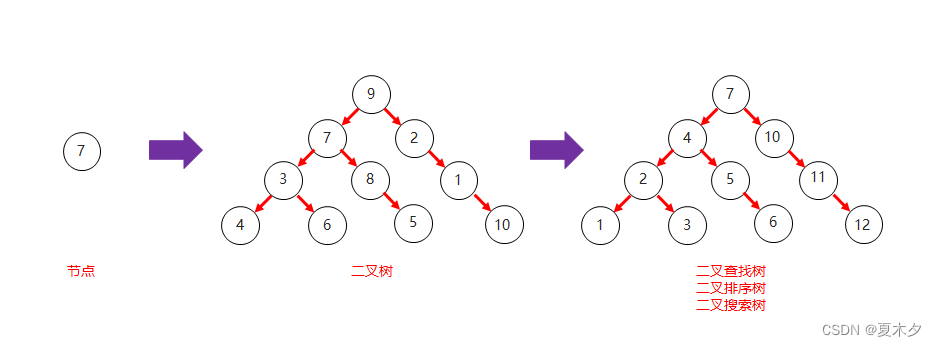
- 二叉查找树和二叉树对比结构图:
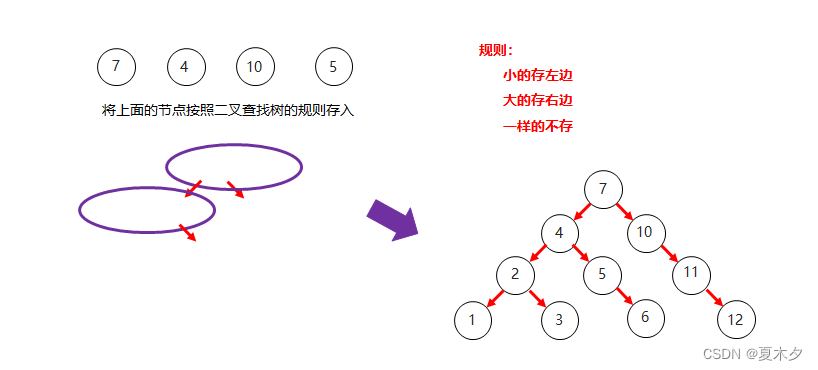
4. 二叉查找树添加节点:
- 小的存左边
- 大的存右边
- 一样的不存
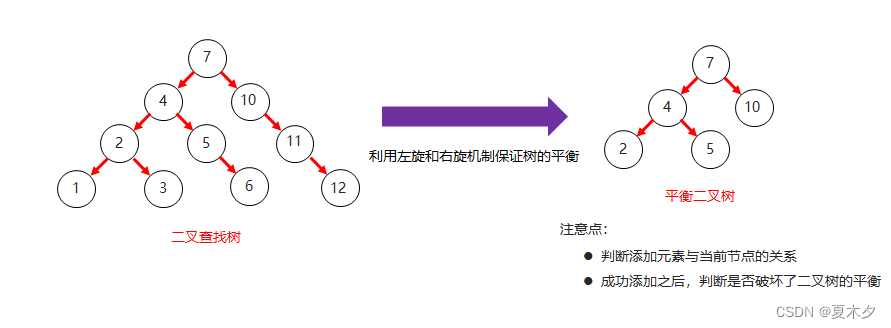
5.3 平衡二叉树
- 平衡二叉树的特点:
- 二叉树左右两个子树的高度差不超过1
- 任意节点的左右两个子树都是一颗平衡二叉树
- 平衡二叉树和二叉查找树对比结构图:
- 平衡二叉树旋转:
-
旋转触发时机
- 当添加一个节点之后,该树不再是一颗平衡二叉树
-
左旋
- 就是将根节点的右侧往左拉,原先的右子节点变成新的父节点,并把多余的左子节点出让,给已经降级的根节点当右子节点
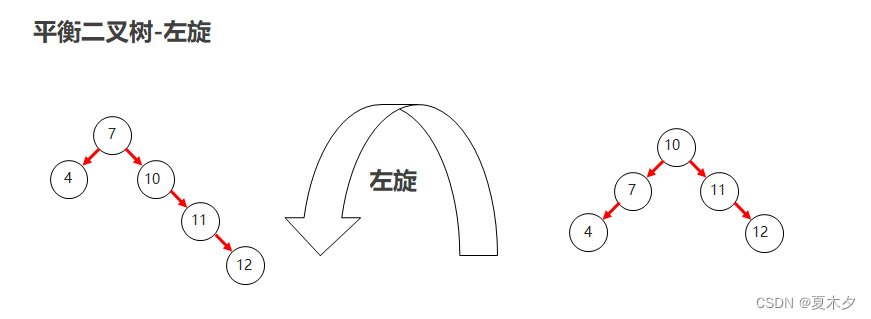
- 就是将根节点的右侧往左拉,原先的右子节点变成新的父节点,并把多余的左子节点出让,给已经降级的根节点当右子节点
-
右旋
- 就是将根节点的左侧往右拉,左子节点变成了新的父节点,并把多余的右子节点出让,给已经降级根节点当左子节点
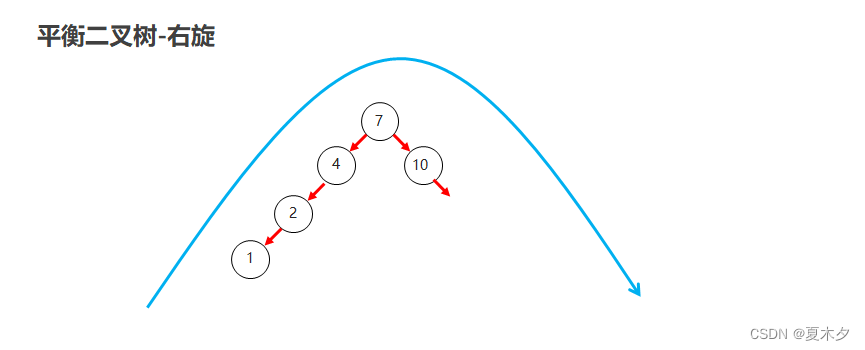
- 就是将根节点的左侧往右拉,左子节点变成了新的父节点,并把多余的右子节点出让,给已经降级根节点当左子节点
- 平衡二叉树旋转的四种情况:
-
左左
- 旋转时机:当根节点左子树的左子树有节点插入,导致二叉树不平衡
- 如何旋转:直接对整体进行右旋即可
-
左右
- 旋转时机:当根节点左子树的右子树有节点插入,导致二叉树不平衡
- 如何旋转:先在左子树对应的节点位置进行左旋,在对整体进行右旋
-
右右
- 旋转时机:当根节点右子树的右子树有节点插入,导致二叉树不平衡
- 如何旋转:直接对整体进行左旋即可
-
右左
- 旋转时机:当根节点右子树的左子树有节点插入,导致二叉树不平衡
- 如何旋转:先在右子树对应的节点位置进行右旋,在对整体进行左旋
5.4 红黑树
- 红黑树概念:
- 红黑树是一种自平衡的二叉查找树,是计算机科学中用到的一种数据结构。
- 1972年出现,当时被称之为平衡二叉B树,后来,1978年被修改为如今的“红黑树”。
- 红黑树的特点:
- 也称平衡二叉B树,是一种特殊的二叉查找树
- 每一个节点上都有存储位表示节点的颜色,可以是红或者黑
- 红黑树不是高度平衡的,它的平衡是通过“自己的红黑规则”进行实现的
- 红黑规则:
- 每一个节点或是红色的,或者是黑色的
- 根节点必须是黑色
- 如果一个节点没有子节点或者父节点,则该节点相应的指针属性值为 Nil,这些 Nil 视为叶节点,每个叶节点 Nil 是黑色的
- 如果某一个节点是红色,那么它的子节点必须是黑色(不能出现两个红色节点相连 的情况)
- 对每一个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点
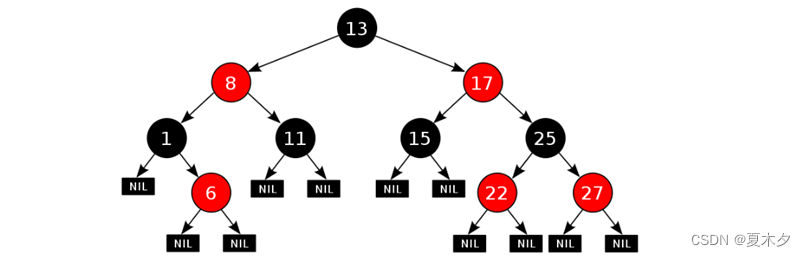
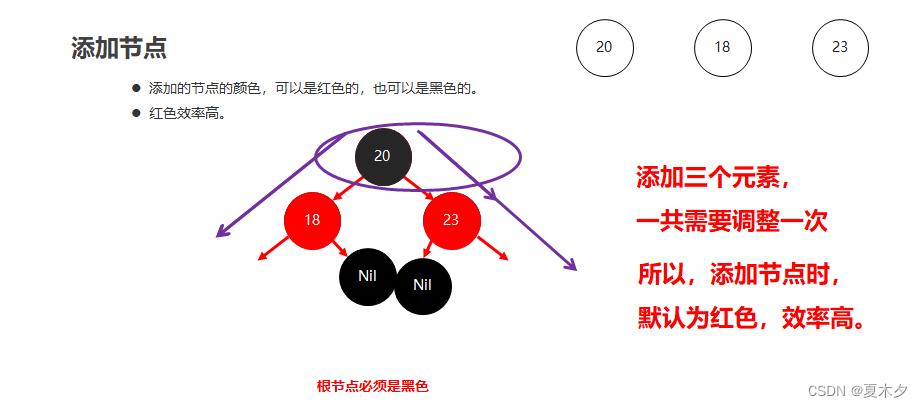
- 红黑树添加节点的默认颜色
- 添加节点时,默认为红色,效率高(如果默认为黑色,添加三个元素,一共需要调整两次 )
- 红黑树添加节点后如何保持红黑规则
- 根节点位置
- 直接变为黑色
- 非根节点位置
- 父节点为黑色
- 不需要任何操作,默认红色即可
- 父节点为红色
- 叔叔节点为红色
- 将“父节点”设为黑色,将“叔叔节点”设为黑色
- 将“祖父节点”设为红色
- 如果“祖父节点”为根节点,则将根节点再次变成黑色
- 叔叔节点为黑色
- 将“父节点”设为黑色
- 将“祖父节点”设为红色
- 以“祖父节点”为支点进行旋转
- 叔叔节点为红色
- 父节点为黑色
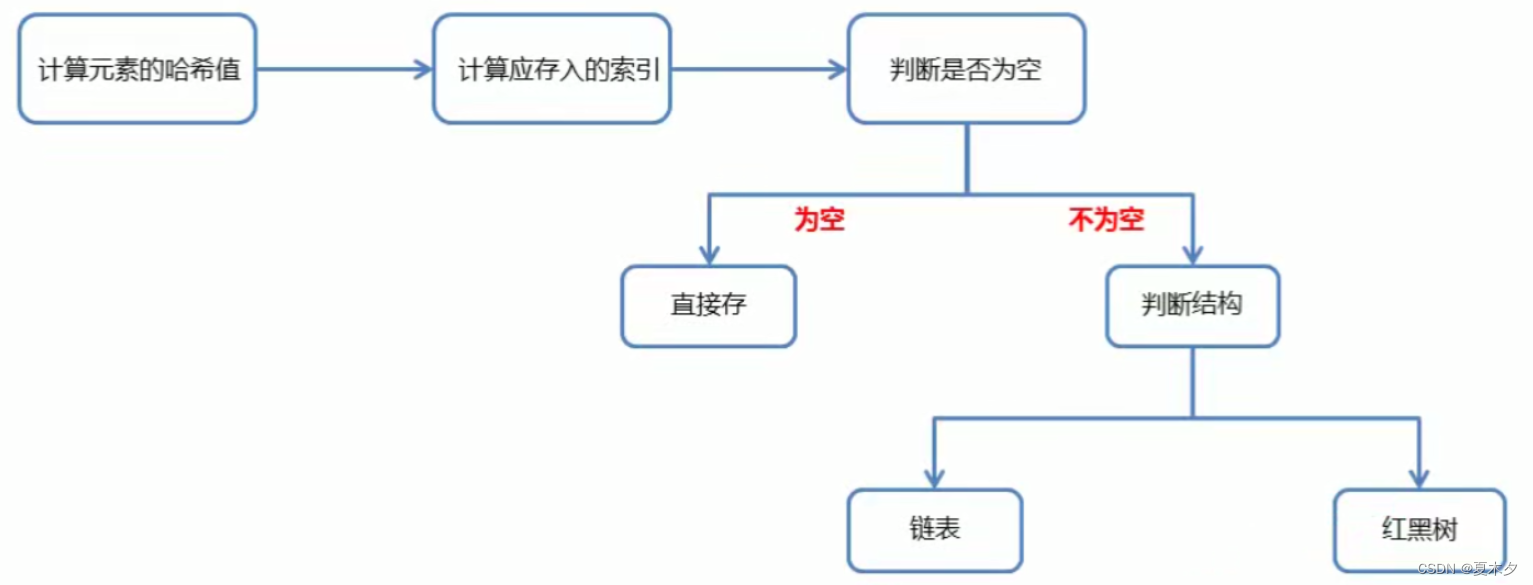
6 哈希表
哈希表
- JDK8之前,底层采用
数组 + 链表实现
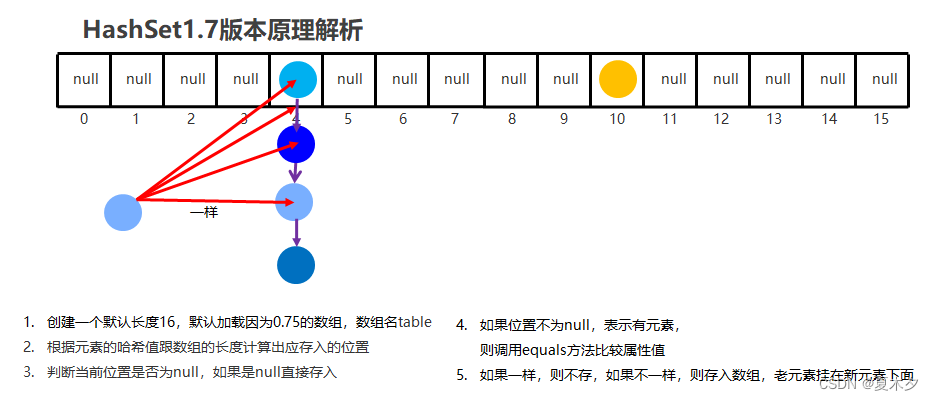
加载因子:本例中,当数组里面存了16*0.75=12个元素的时候,数组就会扩容为原来的两倍
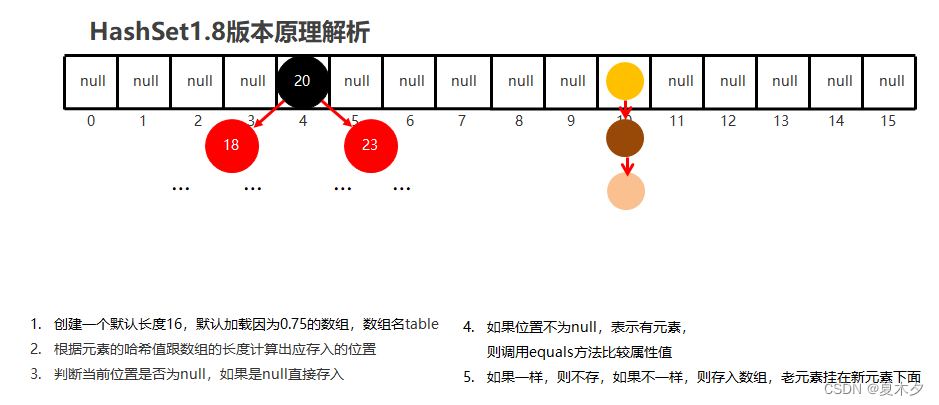
- JDK8之后,底层进行了优化,由
数组 + 链表 + 红黑树实现- 节点个数少于等于8个:
数组 + 链表 - 节点个数多于8个:
数组 + 红黑树(红黑树基于二叉排序树,小的跟左边比,打的跟右边比,提高了效率)
- 节点个数少于等于8个:
当挂在下面的元素过多,那么不利于添加,也不利于查询,所以在JDK8以后,当俩表长度超过8的时候,自动转换为红黑树,存储流程不变。