强化学习基本概念
- 前言
- 1、State、Action、Policy等
- ① State
- ② Action
- ③ State transition
- ④ State transition probability
- ⑤ Polity
- 2、Reward、Return、MDP等
- ① Reward
- ② Trajectory and return
- ③ Discounted return
- ④ Episode
- ⑤ MDP
- 总结:
前言
本文来自西湖大学赵世钰老师的B站视频。本节课主要介绍强化学习的基本概念。
1、State、Action、Policy等
本文中会广泛使用的一个例子是网格世界,有一个机器人在里边走,每一个小的网格有不同的类型,白色的网格是可以进去的,黄色的网格是禁止进入的,target是我们希望它能够进到的网格,此外,这个网格是有边界的,3x3。要求是机器人可以在相邻的两个网格移动,不能斜着移动。这个机器人的任务是找到一个“good way”从Start到target。如下所示:
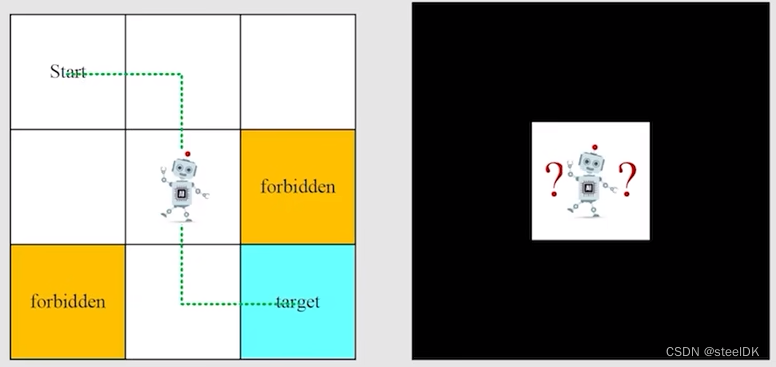
下面用这个例子来介绍本节课中的第一个概念:State
① State
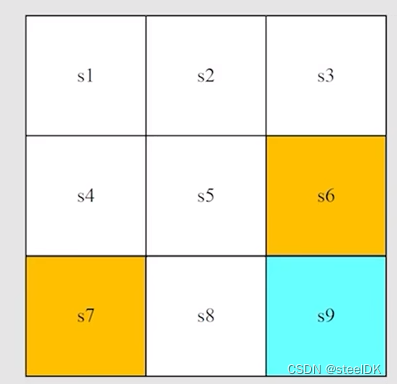
State实际上描述的就是agent相对于环境的状态。(The status of the agent with respect to the environment)
在网格世界这个任务中,state指的就是机器人的位置,则共有s1,s2,…s9个位置,如上图所示。这里每个state用的是一个二维坐标表示,即(x,y),如果对于一些比较复杂的场景,可能还要加上速度和加速度。
状态空间就是所有状态的集合,用S={s1,s2,…s9}。
② Action
Action就是在每个状态可采取的行动。在网格世界任务中,每个状态有五个动作,记作a1,… a5。a1是往上走,a2是往右走,a3是往下走,a4是往左走,a5是原地不动。
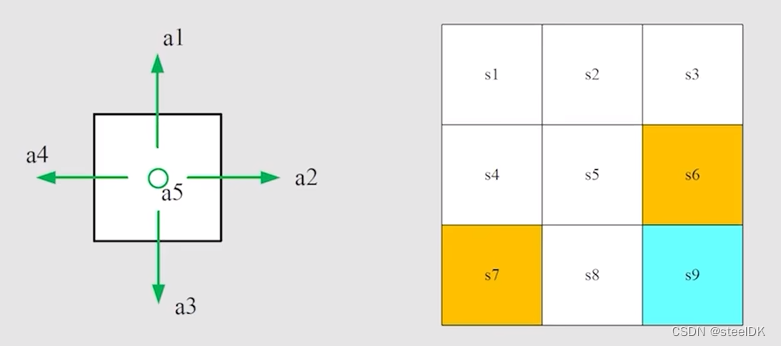
Action space是所有可能的动作的集合,用A(si)={a1,… a5}表示。
③ State transition
当我们采取一个行动的时候,智能体agent就会从一个状态移动到另一个状态,这个过程叫做state transition。举个例子:
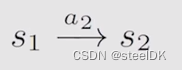
当我们在状态s1,采取行动a2,那么下一个状态就会变成s2,如下所示。
我们可以利用一个表格来描述状态转变,如下图所示:
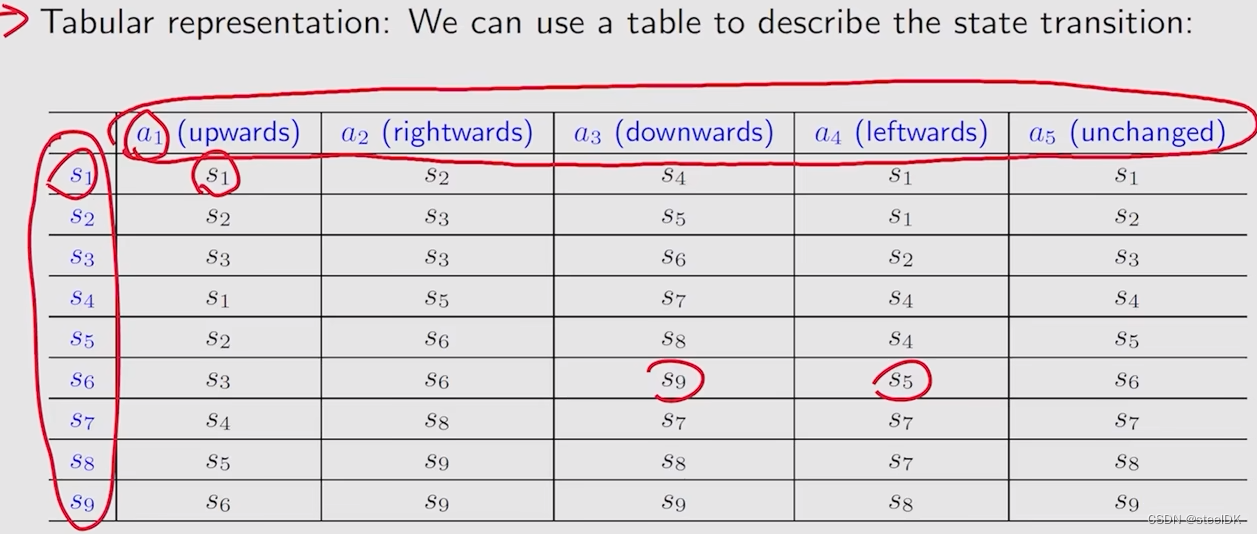
表格虽然比较直观,但是在实际中却应用受限,因为它只能表示这种确定性的情况。比如,我们在状态s1,执行动作a4,即向左走,那么机器人会撞到墙弹回来,弹回来仍然为s1,也有可能弹到s4或者s7,这种不确定性无法用表格表示。因此我们更一般的方法是用state transition probability。
④ State transition probability

用条件概率来表示下一状态发生的可能性。
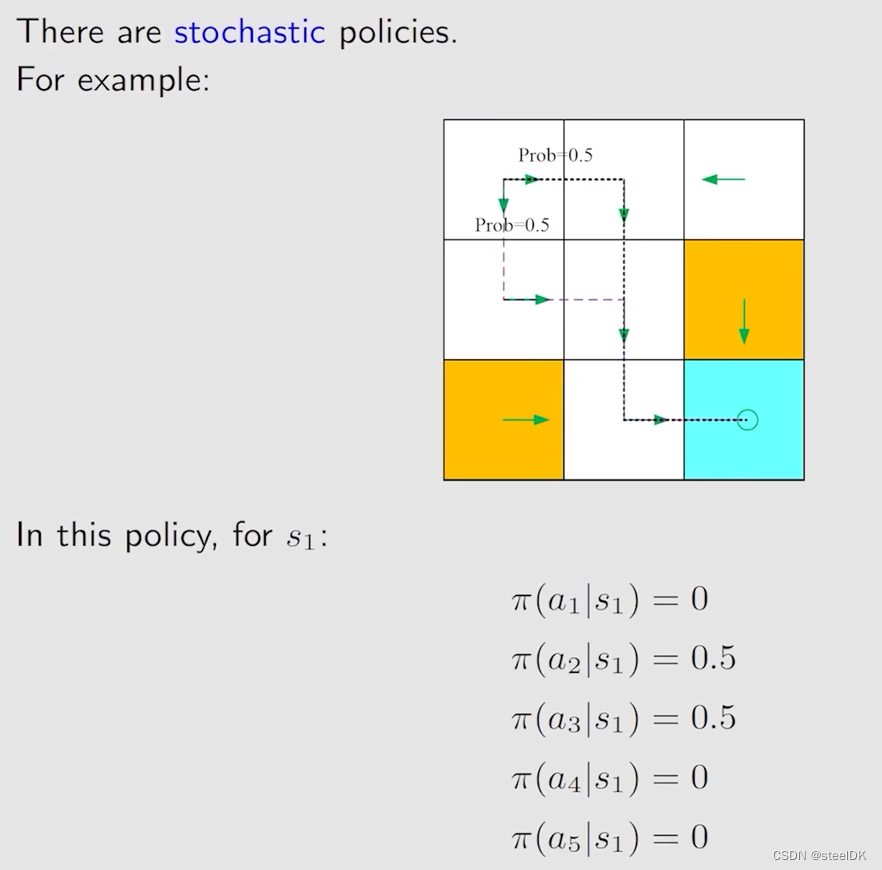
⑤ Polity
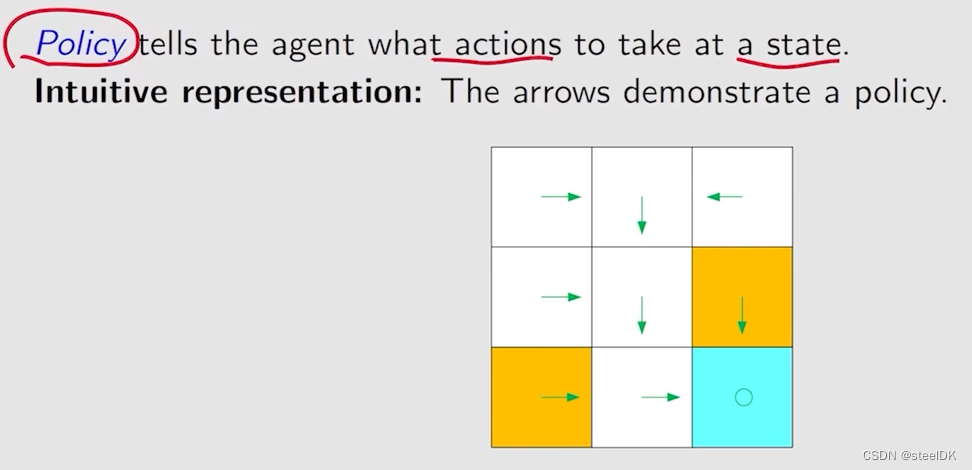
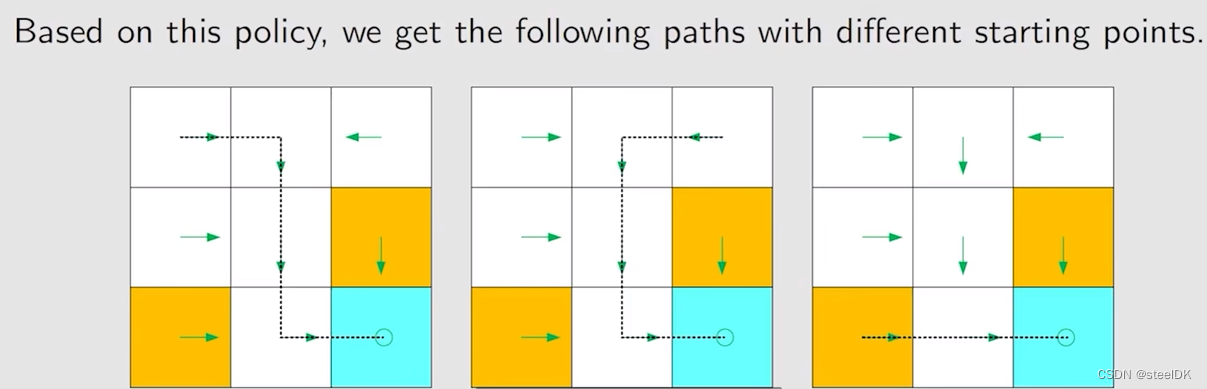
上图种圆圈代表原地不动,策略用箭头表示。箭头所表示的情况有限,现实中我们需要能够描述复杂情况的一般化方法:

用π表示策略(在强化学习中,π这个符号统一用来表示策略),π就是一个条件概率,它指定了任何一个状态下,任何一个action的概率,是一个不确定的概率。
策略可以用表格的形式表示:
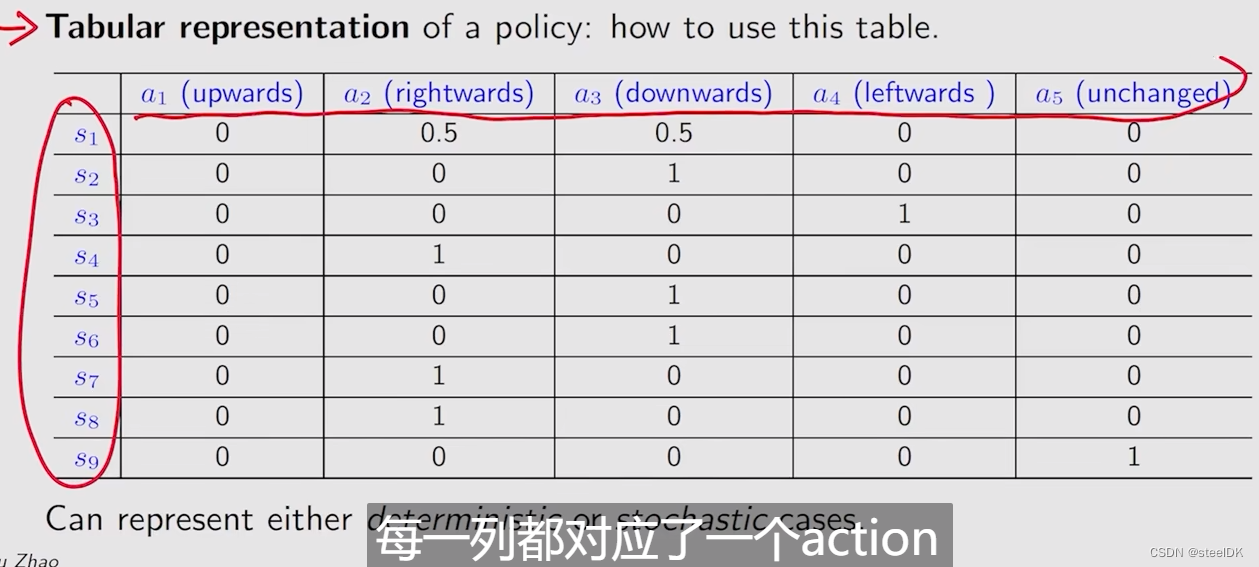
每一行都对应了一个动作,每一列都对应一个状态。比如,在状态s1下,有50%的概率往右走,50%的概率往下走,那么在编程中如何实现呢?即使创建一个0到1之间的均匀分布,然后从中随机取一个数x,当x属于0~ 0.5时,就采取a2,x属于0.5~1时采取a1。
2、Reward、Return、MDP等
① Reward
reward是强化学习中非常独特的概念。Reward是采取一个动作之后得到的一个实数(标量)。如果这个实数是正数,代表我们对智能体的这个行为是鼓励的,如果这个实数是负数,代表我们不希望这样的事情发生,是一个惩罚。这里引出两个问题,一个问题是Reward为0,为0代表一定程度的奖励。还有一个问题是我们能不能用正数表示惩罚,负数表示激励,答案是可以,这本质上是数学上的一些技巧,本质上是一样的。对于网格世界,其Reward如下:
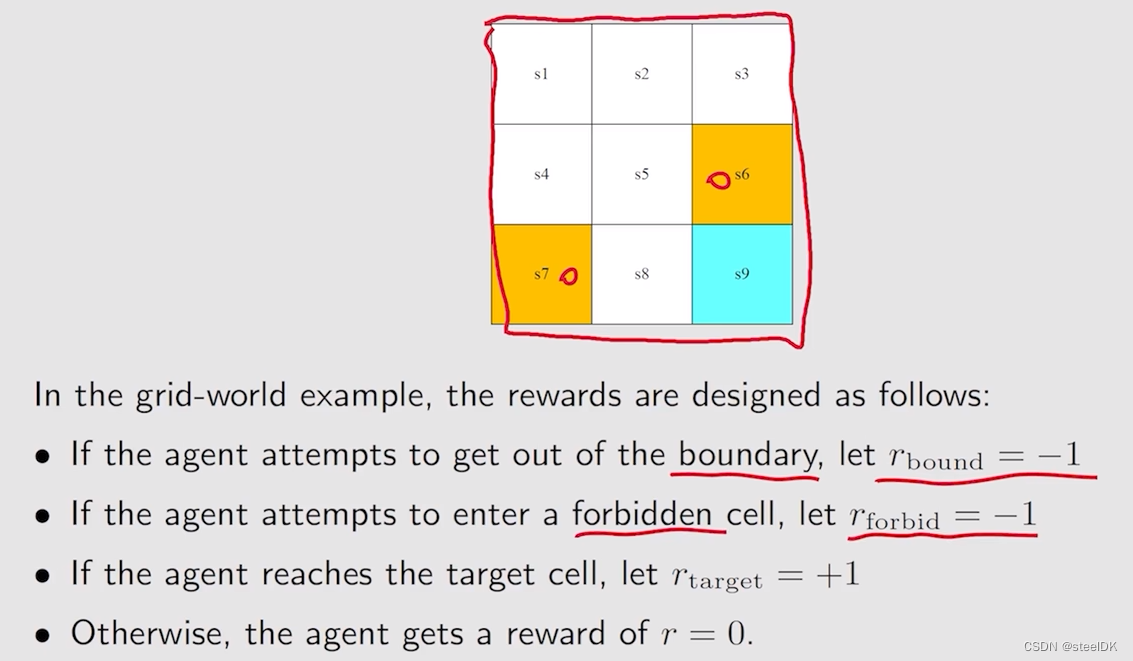
Reward可以理解为human-machine interface,是人类和机器交互的一种手段,通过Reward我们可以引导agent什么可以做,什么不能做。我们也可以用表格对Reward进行表示,如下图:

表格的形式智能表示一种确定的实例,如果采取一个动作,不确定其奖励,则可以通过数学方法(条件概率)进行表示:

② Trajectory and return
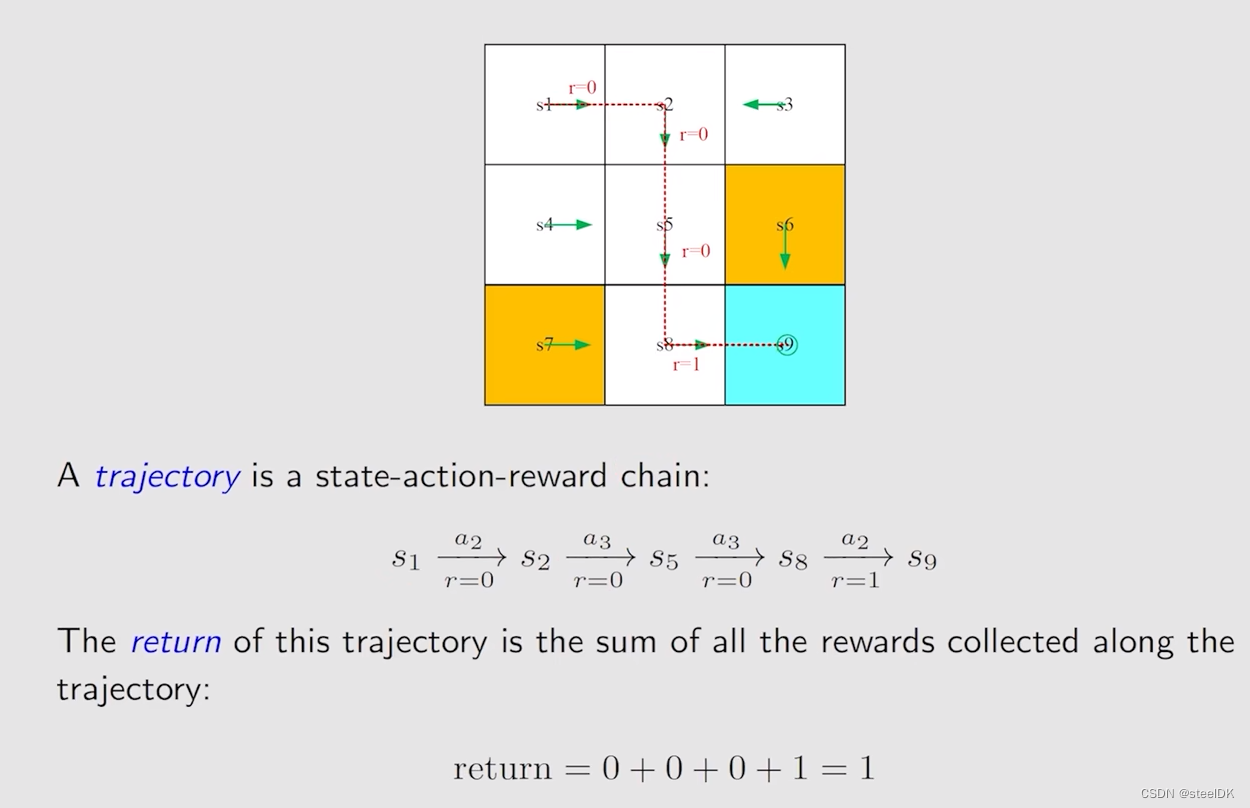
return就是把所有的reward加起来的总和。
③ Discounted return
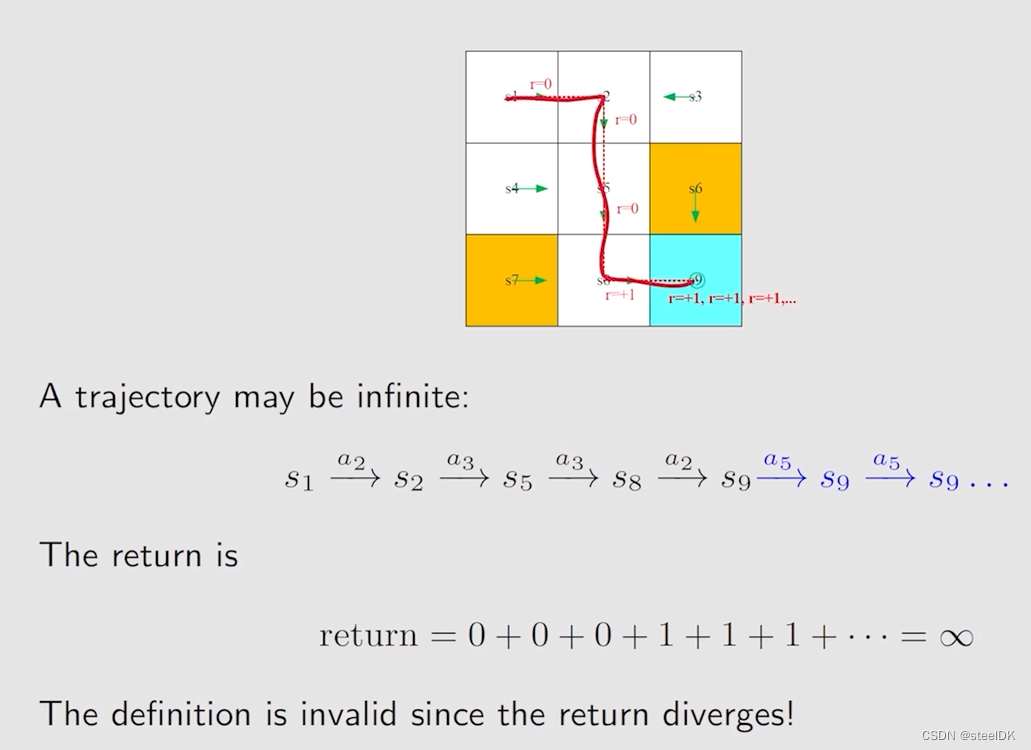
从状态s1到状态s9,到了s9之后,策略还在进行,这导致了return为无穷大。为了避免这一情况,通过引入discount rate来解决:

如果减少γ,它就会更加注意最近的一些reward,如果增加γ,它就会更加注意长远的reward。
④ Episode
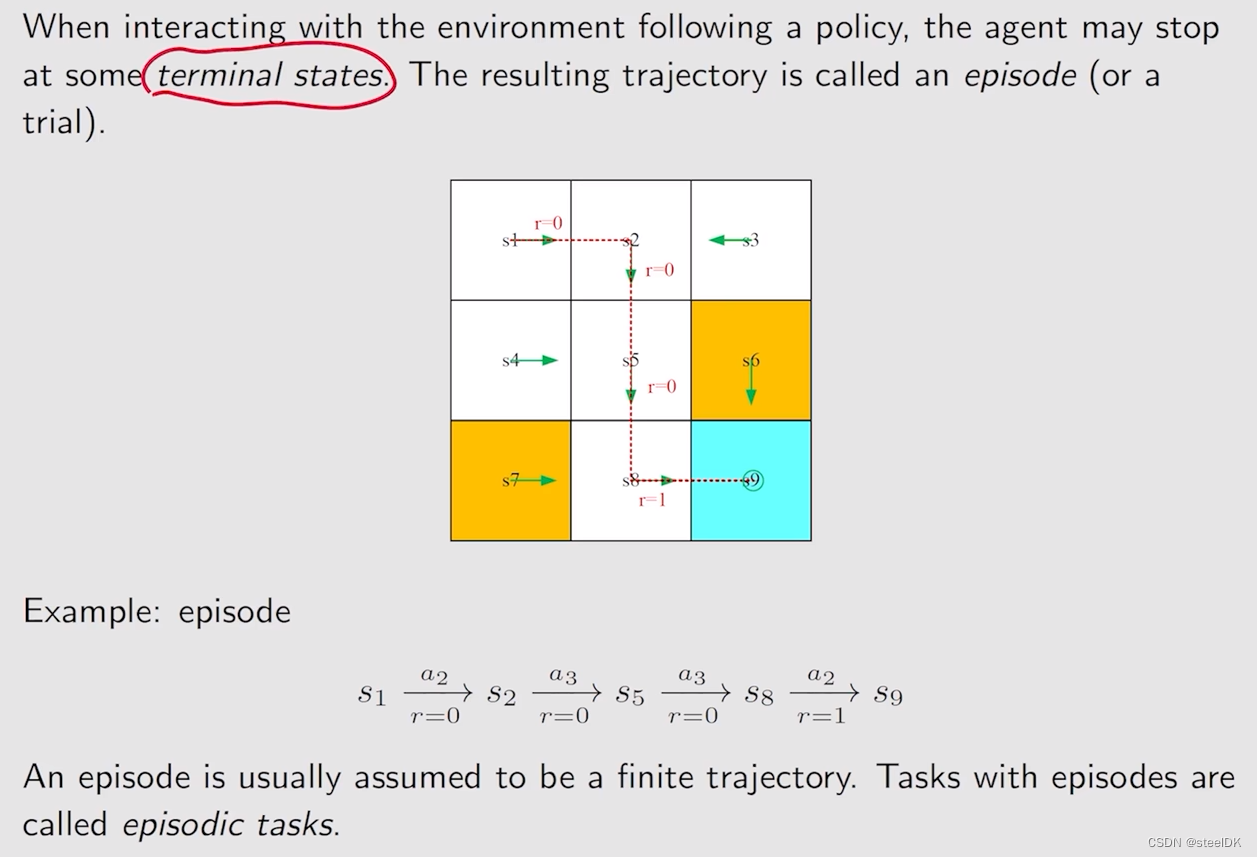
episode实际上就是状态s1到s9,状态s9称为terminal states,在terminal states之后就停止了,不在进行了,这就叫episode。
但有些任务没有terminal states,这意味着agent和环境的交互会永远交互下去,这样的任务称为continuing tasks。

⑤ MDP
Markov decision process(MDP),是马尔可夫过程。MDP有很多要素,第一个要素是它包含了很多集合Sets,包括State、Action、Reward。第二个要素是Probability distribution,第三个要素是Polity,第四个要素是Markov property:memoryless property,与历史无关,这是MDP本身的性质。详见如下:

可以用Markov decision process这三个词来描述马尔可夫过程,首先Markov对应Markov property,decision对应Policy,是一个策略,process是从一个状态跳到另一个状态,采取什么样的action等等,这些都由Sets(State、Action、Reward)和Probability distribution描述。那么网格世界就可以用Markov process来描述:
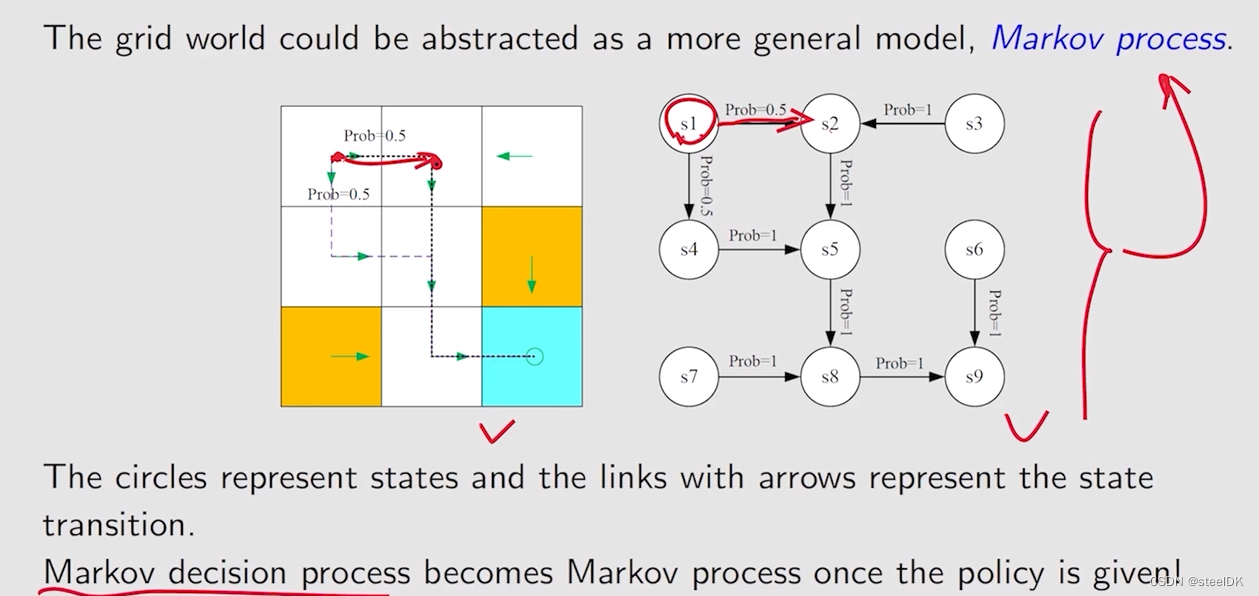
上图右图描述的是Markov process,如果policy是给定的话,就变成了Markov decision process。
总结:

下节介绍贝尔曼公式。