计算机视觉与深度学习-卷积神经网络-纹理表示卷积神经网络-纹理表示-[北邮鲁鹏]

目录标题

参考文章
纹理定义
纹理的分类
- 规则纹理
- 随机纹理
纹理的表示方法
- 基于卷积核组
- - 思路
  - 什么卷积核组
  - - 卷积核类型（边缘、条形、点状）
    - 卷积核尺度（3~6个尺度）
    - 卷积核的方向
    - 卷积核组的设计
  - 表示步骤
  - - 步骤一：设计卷积核组。
    - 步骤二：利用卷积核组对图像进行卷积操作获得对应的特征响应图组。
    - 步骤三：利用特征响应图的某种统计信息来表示图像中的纹理。
  - 总结
纹理表示注意事项
纹理表示与卷积神经网络的联系

参考文章

计算机视觉与深度学习-05-纹理表示&卷积神经网络-北邮鲁鹏老师课程笔记

纹理定义

纹理是指物体表面的视觉和触觉特征，它描述了物体表面的细节、图案和结构。
计算机图形学中的纹理既包括通常意义上物体表面的纹理即使物体表面呈现凹凸不平的沟纹，同时也包括在物体的光滑表面上的彩色图案，通常我们更多地称之为花纹。

在这里插入图片描述
纹理是由于物体表面的物理属性的多样性而造成的，物理属性不同表示某个特定表面特征的灰度或者颜色信息不同，不同的物理表面会产生不同的纹理图像，因而纹理作为图像的一个极为重要的属性，在计算机视觉和图像处理中占有举足轻重的地位。

纹理是图像中特征值强度的某种局部重复模式的宏观表现。然而，对于自然纹理图像而言这种重复模式往往是近似的和复杂的，难以用语言描述，而人类对纹理的感受多是与心理效果相结合的，因此，迄今都没有一个对纹理的正式的、广泛认可的和一致的定义。

Hawkins曾经对纹理给出了一个比较详细的描述,他认为纹理有三个主要的标志:

某种局部的序列性在比该序列更大的区域内不断重复
序列是由基本元素非随机排列组成的
各部分大致是均匀的统体,在纹理区域内的任何地方都有大致相同的结构尺

纹理的分类

规则纹理

在这里插入图片描述
通常都是人造

随机纹理

在这里插入图片描述
自然界通常都是随机纹理

纹理的表示方法

基于卷积核组

思路

利用卷积核组提取图像中的纹理基
利用基元的统计信息来表示图像中的纹理

什么卷积核组

卷积核组又称为纹理滤波器组。

卷积核类型（边缘、条形、点状）

边缘：高斯一阶偏导核。例：黑|白，白|黑。
条形：高斯二阶偏导核。例：白|黑|白，黑|白|黑。
点状：。例：周围白中间黑，周围黑中间白。

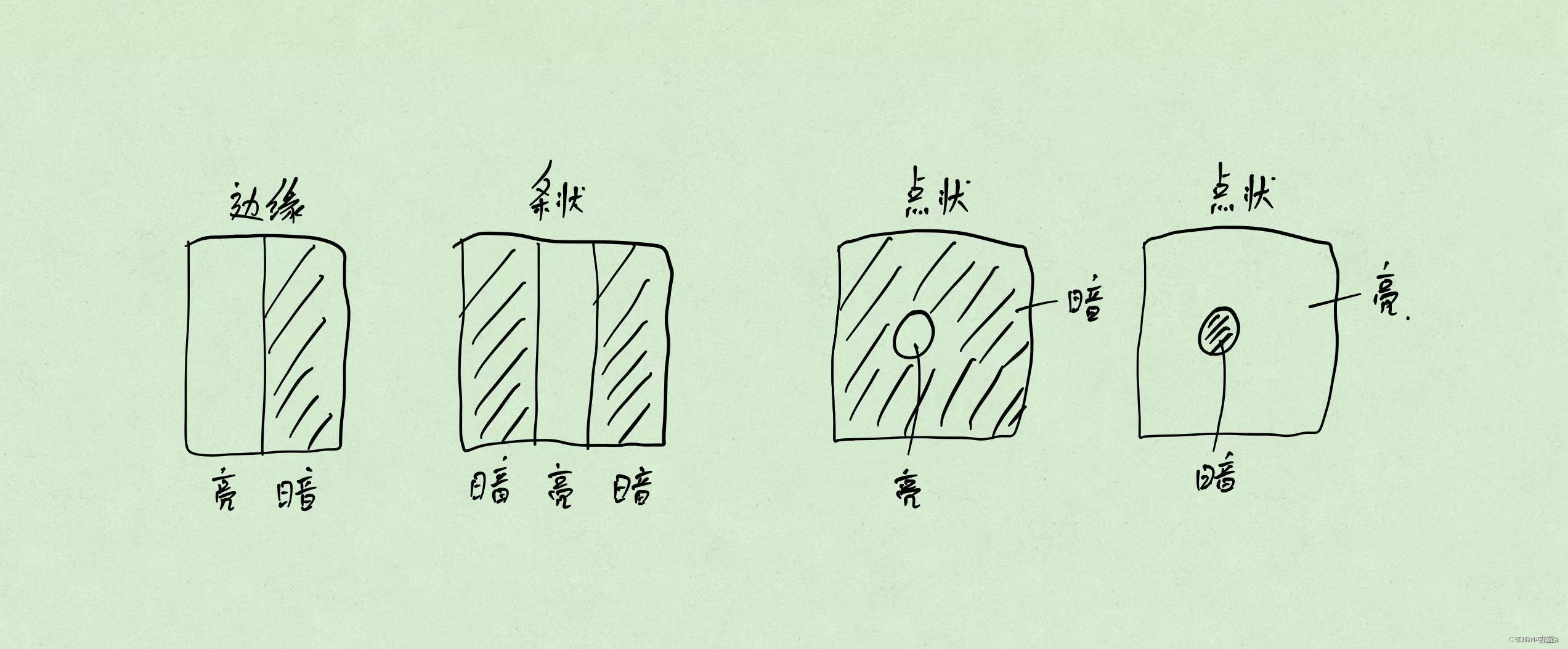
在这里插入图片描述

卷积核尺度（3~6个尺度）

大尺度，提取粗粒度边。
小尺度，提取细粒度边。

卷积核的方向

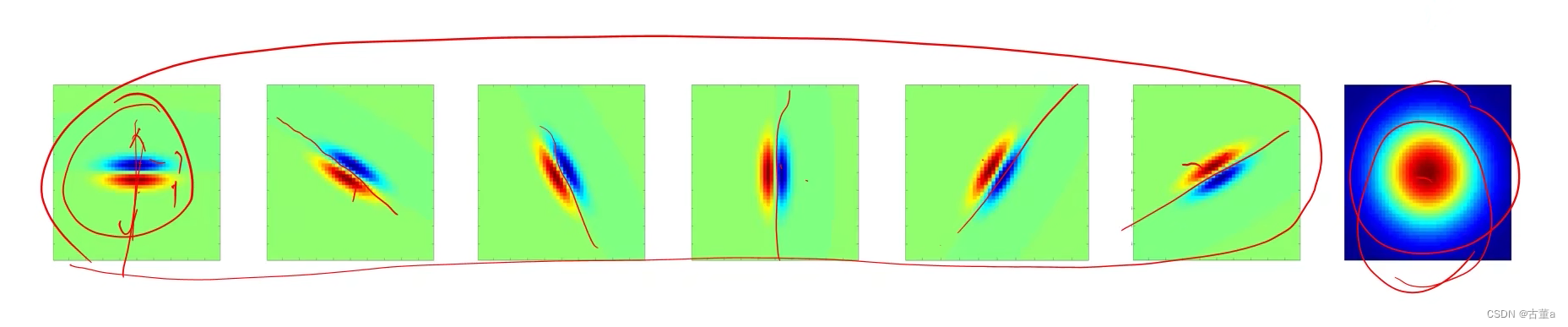
在这里插入图片描述
前6个卷积核检测是否存在边缘及边缘的方向。
第1个卷积核检测图像中是否有x方向的边缘。（高斯卷积核对y求导）
第4个卷积核检测图像中是否有y方向的边缘。（高斯卷积核对x求导）
第7个卷积核检测图像中是否有斑状基元。

第1个卷积核检测图像中是否有x方向的边缘。（高斯卷积核对y求导）
在这里插入图片描述
第7个卷积核检测图像中是否有斑状基元

卷积核组的设计

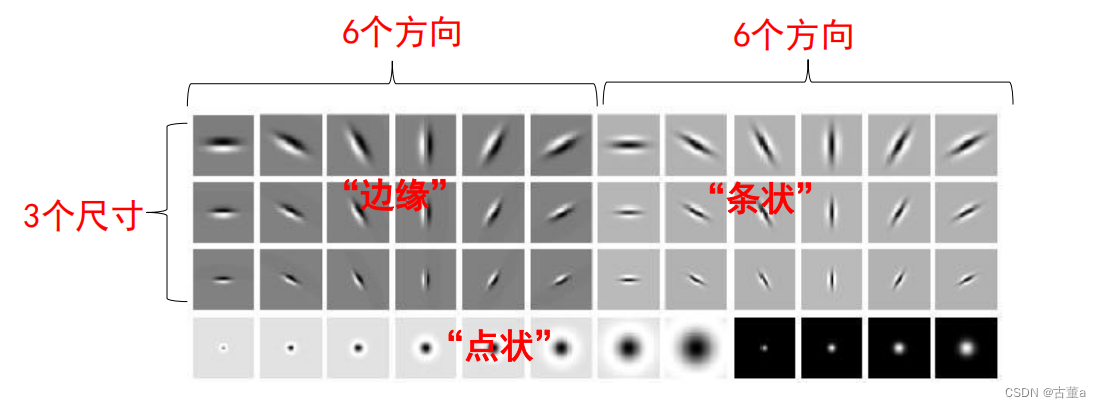
在这里插入图片描述
48个卷积核组

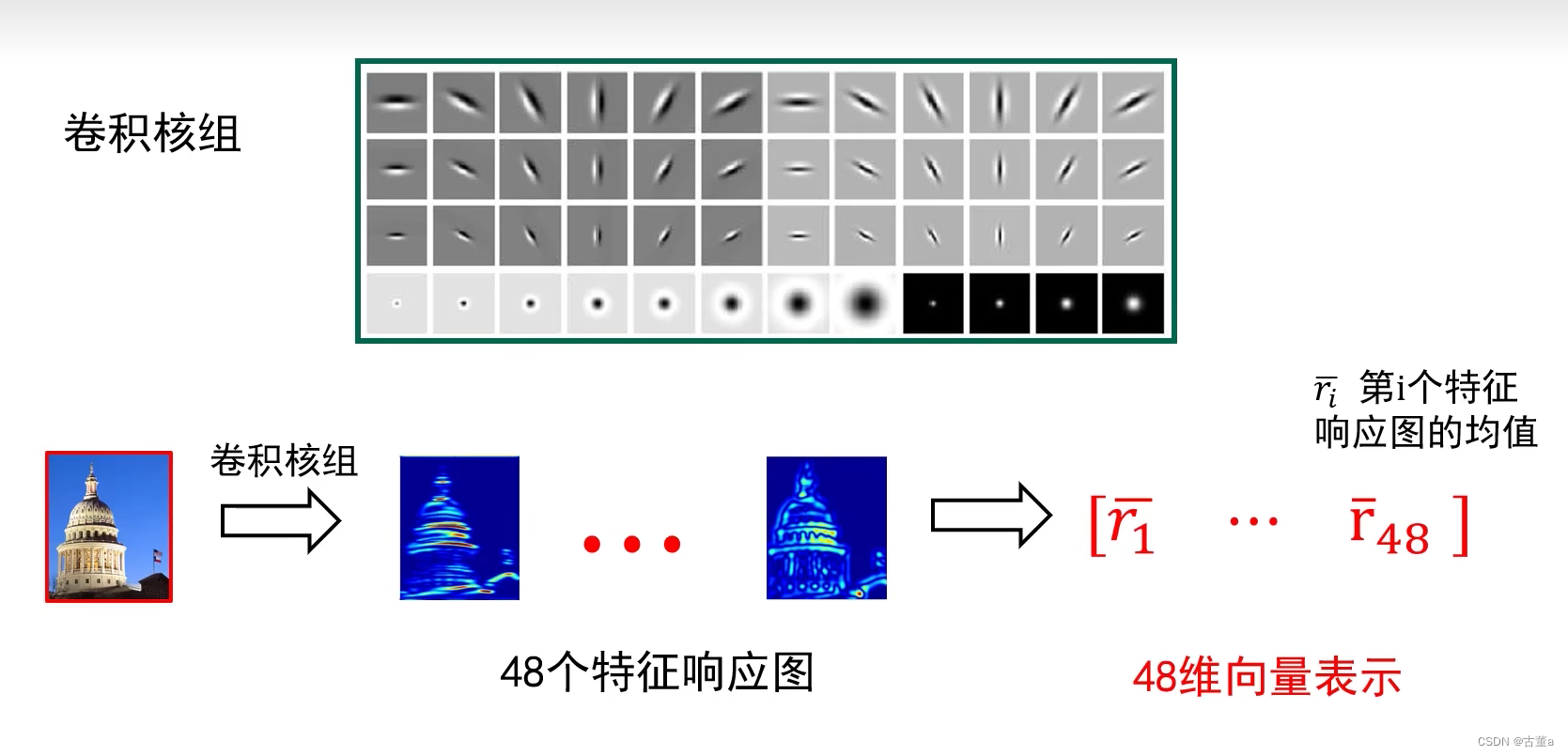
表示步骤

步骤一：设计卷积核组。

在这里插入图片描述

步骤二：利用卷积核组对图像进行卷积操作获得对应的特征响应图组。

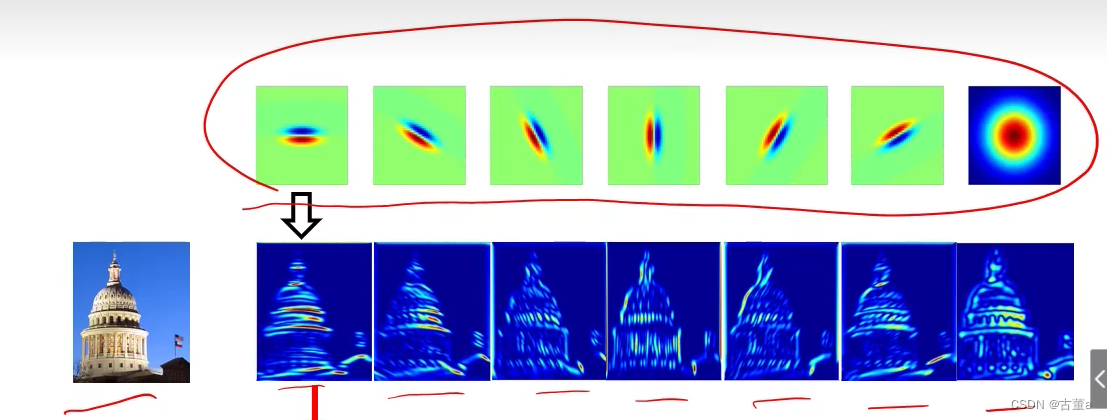
在这里插入图片描述

步骤三：利用特征响应图的某种统计信息来表示图像中的纹理。

方式一（含基元位置信息）
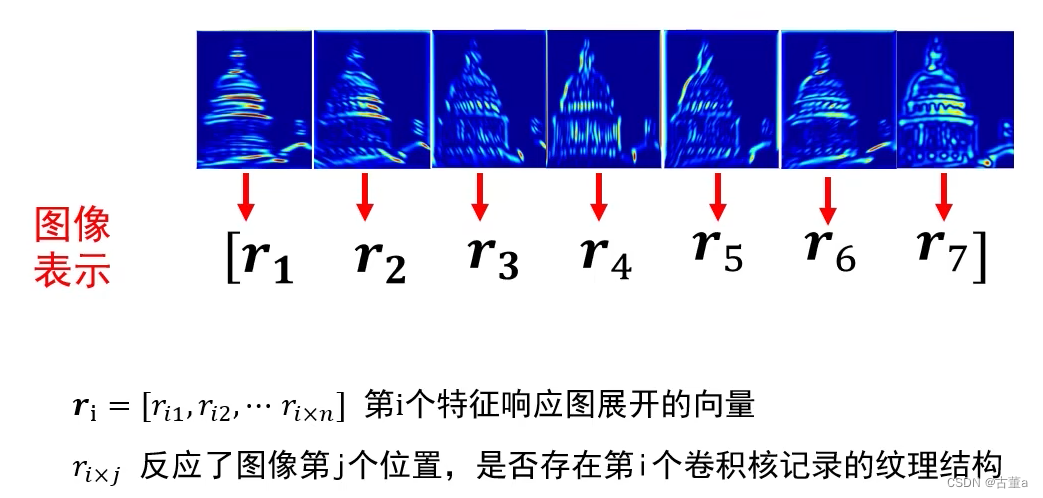
在这里插入图片描述
假设图片是 100 * 100，使用上述含7个卷积核的卷积核组，则该图片每一个像素点表示为 $r_i = [r_{i1},r_{i2},\dots,r_{i 7}]$ ， $r_{imax} = max\{{r_{i1},r_{i2},\dots,r_{i 7}}\}$ 。则 $r_{imax}$ 对应的特征响应图即为该像素点的特征。

其中 $r_i$ 的维度是 10000 * 1， $[r_{i1},r_{i2},\dots,r_{i7}]$ 的维度是 10000 * 7，经过变换后 $[r_{i1},r_{i2},\dots,r_{i7}]$ 的维度为 70000 * 1。

该表示方式的缺点：70000维太复杂。

方式二（忽略基元位置信息）

纹理分类任务中，基元的位置对纹理分类没有影响。

只关注出现了哪种基元对应的纹理以及基元出现的频率，即用特征响应图的平均值表示图像。
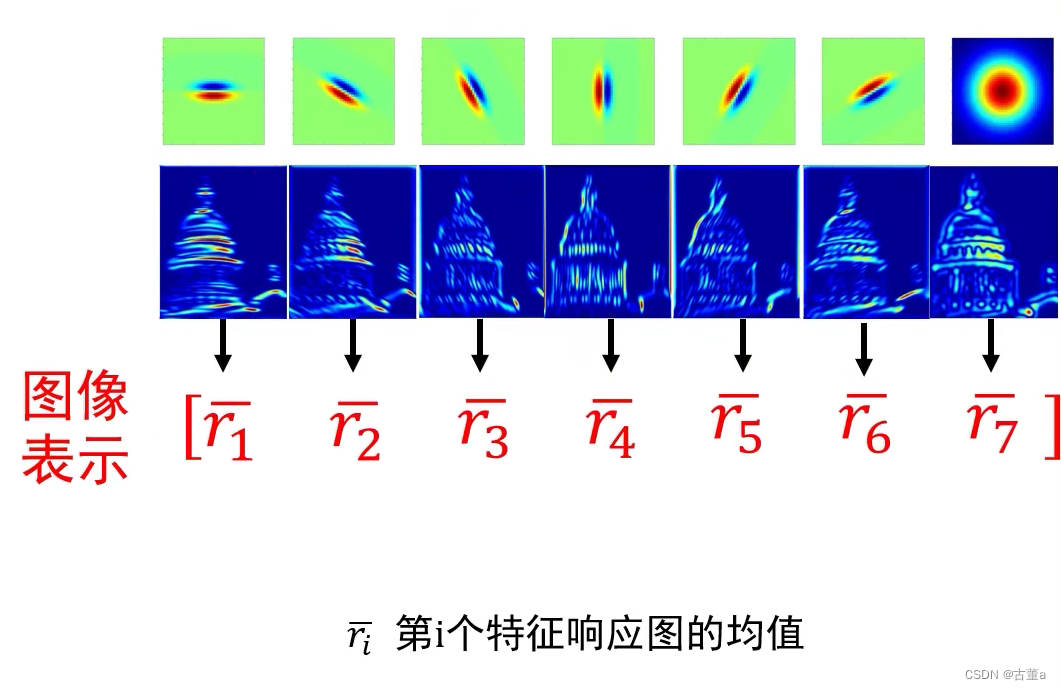
在这里插入图片描述

假设图片是100 * 100，使用上述含7个卷积核的卷积核组，则该图片每一个像素点基元平均值表示为 $\bar r = [ \bar {r_{1}}, \bar r_{2},\dots, \bar r_{ 7}]$ ， $\bar r_{imax} = max\{{\bar r_{1}, \bar r_{2},\dots, \bar r_{7}}\}$ ，则 $r_{imax}$ 对应的特征响应图即为该像素点的特征。

其中 $\bar r_i$ 为第 i 个特征响应图的平均值，其维度是 1 * 1， $\bar r_j$ 的维度是 1 * 7，经过变换后 $\bar r_j$ 的维度为 7 * 1。

举例表示
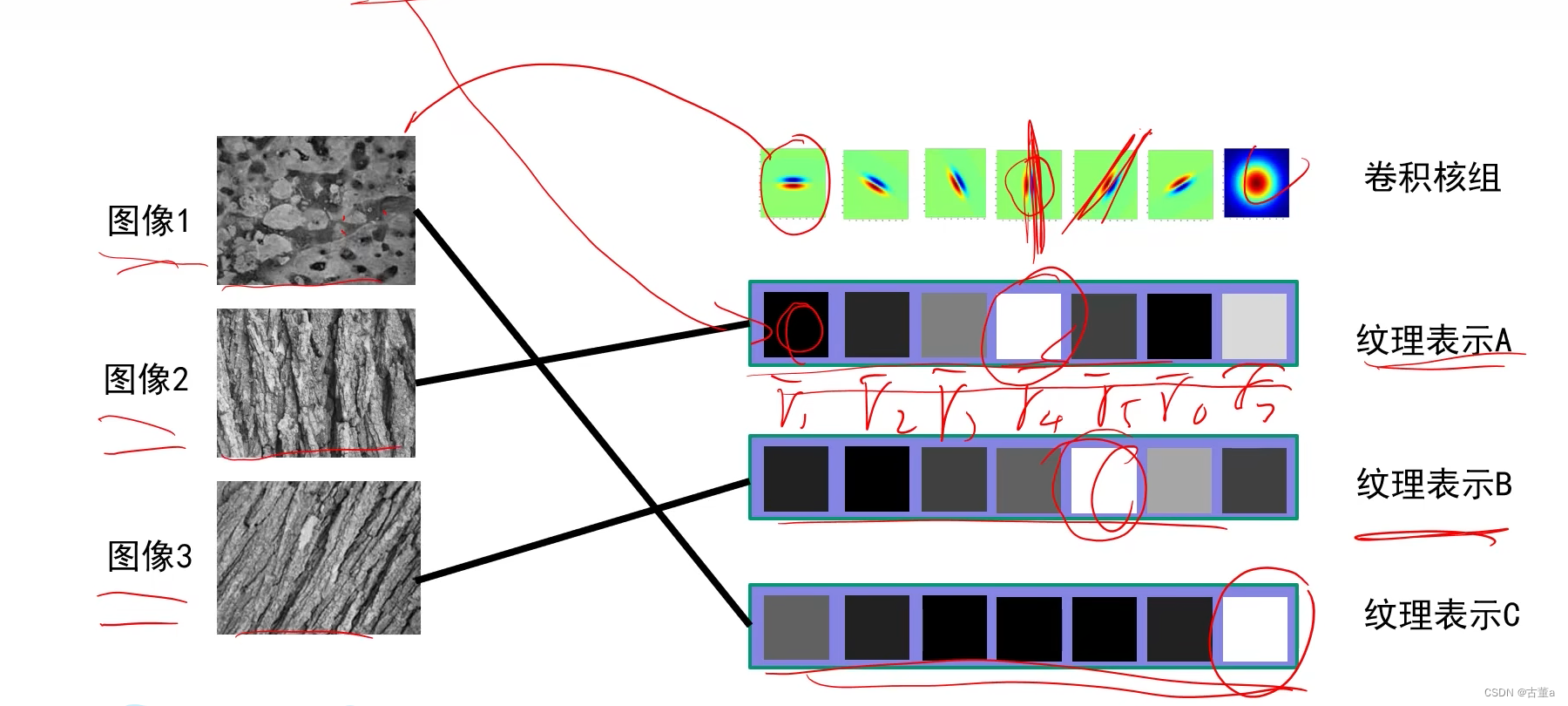
在这里插入图片描述
纹理表示A：r4 比较大，表示y方向的纹理比较多。
纹理表示B：r5 比较大，表示y=x方向的纹理比较多。
纹理表示C：r7 比较大，表示斑点纹理比较多。

总结

设计卷积核组；
利用卷积核组对图像进行卷积操作获得对应的特征响应图组；
利用特征响应图的某种统计信息来表示图像中的纹理。

纹理表示注意事项

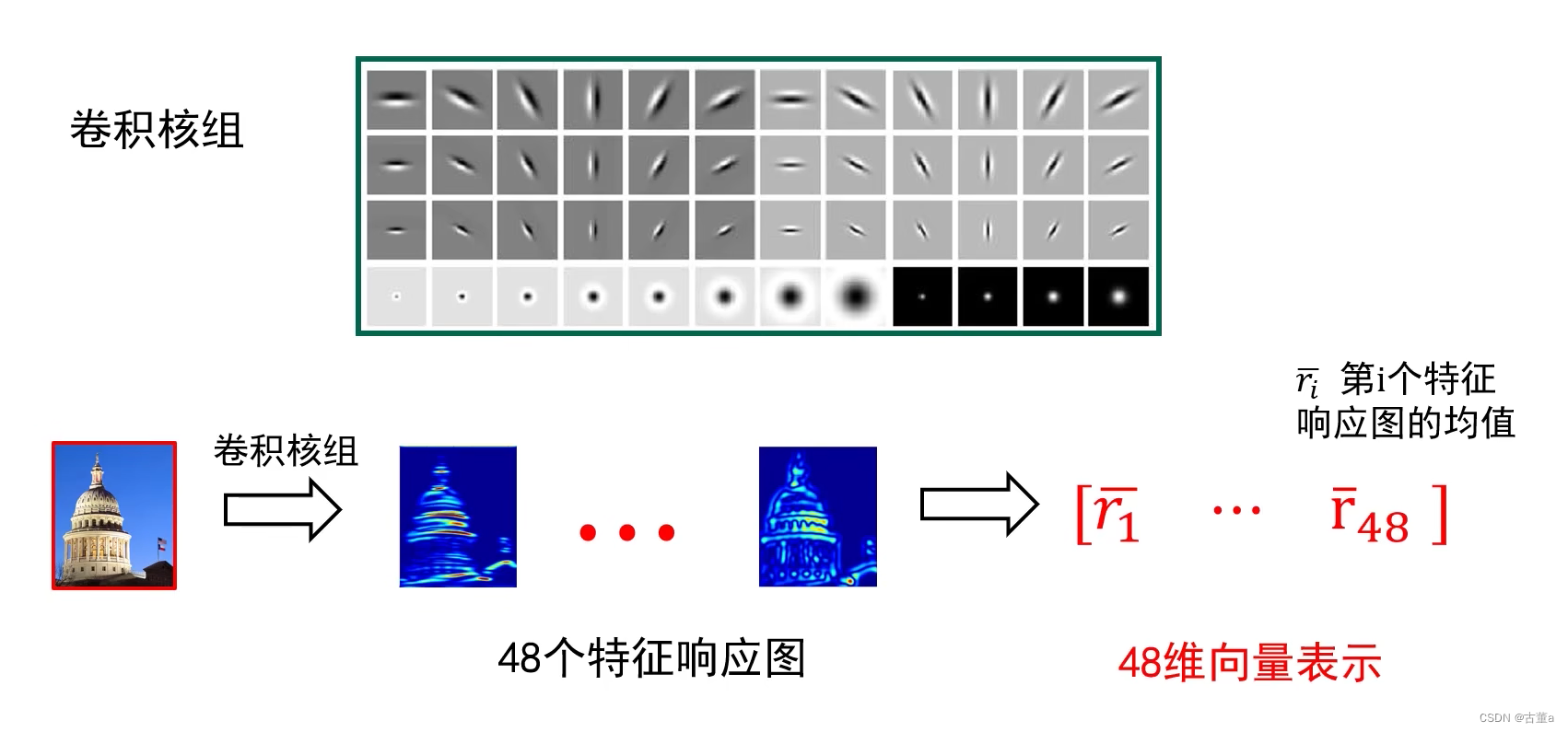
在这里插入图片描述
$\bar r = [\bar r_1,\bar r_2,\bar r_3,\bar r_4,... ,\bar r_{46},\bar r_{47}, \bar r_{48}]$ 中最大值大概率只有一个，因为一张图像包含一个卷积核组所表示的纹理的概率大，包含多个卷积核组所表示纹理的概率很小，所以这个48维向量是稀疏向量。