一、简介
股票上涨和下跌,创造出像海浪一样难以预测的模式和走势。然而,就像科学家通过了解下面的水流来预测波浪的运动一样,我们也可以使用类似的工具破译股票市场的一些模式。
通过利用小波变换的力量,我们深入表面,试图揭示驱动股价的深层原因。这段旅程不仅仅涉及数字和数据;还涉及数字和数据。它是将抽象的东西转化为有形的东西,利用股票看似不稳定的行为并找到节奏和原因。
2. 小波变换理论
从本质上讲,小波是一种短暂的振荡,其能量集中在时间上,确保其寿命短暂且持续时间有限。想象一下敲击鼓:产生的声音很强烈,但很快就消失了。小波的这种短暂特性使它们非常适合分析非平稳的金融信号(即它们的统计属性随时间变化)。小波变换类似于提供显微镜来查看股票数据的复杂细节,捕捉其大趋势和微小波动。
2.1 为什么不用傅里叶变换?
许多人可能会想,为什么不直接使用傅里叶变换,这是一种非常流行的信号分析工具呢?傅立叶变换将信号分解为其组成的正弦曲线。然而,它的致命弱点是无法同时提供时间和频率信息。虽然它可以告诉我们存在的频率,但它通常会忽略它们何时发生。与傅里叶变换不同,小波变换捕获频率和时间,提供信号的时频表示。
2.2 小波变换的本质
在数学上,小波变换可以表示为:
![]()
在哪里:
- W是我们比较的结果,为我们提供了相似性的度量。
- f ( t ) 代表我们的库存数据。
- ψ ( t ) 是所选的小波模式。
本质上,我们在股票数据f ( t ) 上移动小波ψ,寻找它们对齐良好的位置。这给我们提供了小波系数W ( b ),它告诉我们股票数据在每个时间点与小波的匹配程度。简而言之,任何给定点的匹配越好, W值就越高。
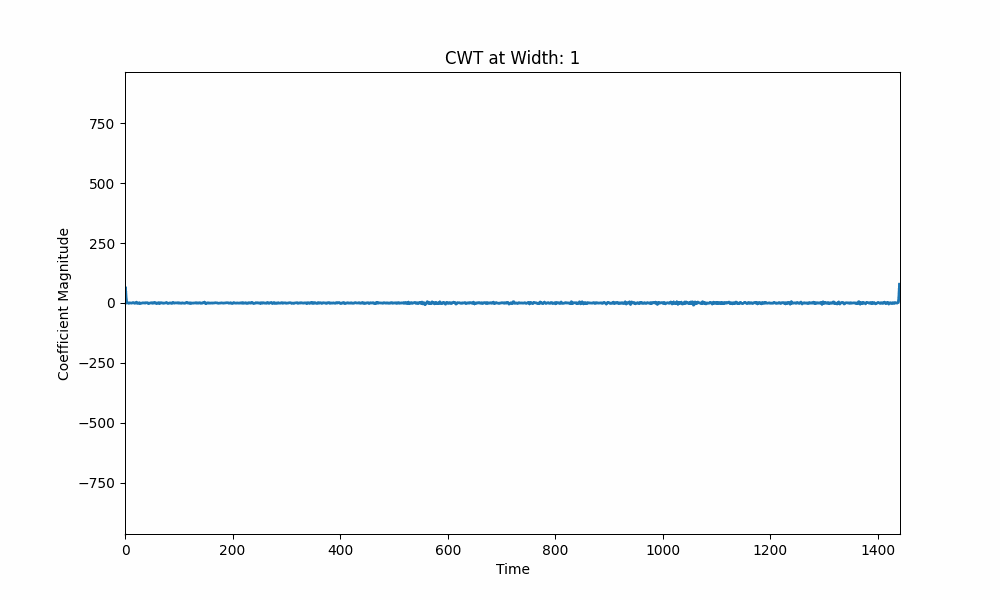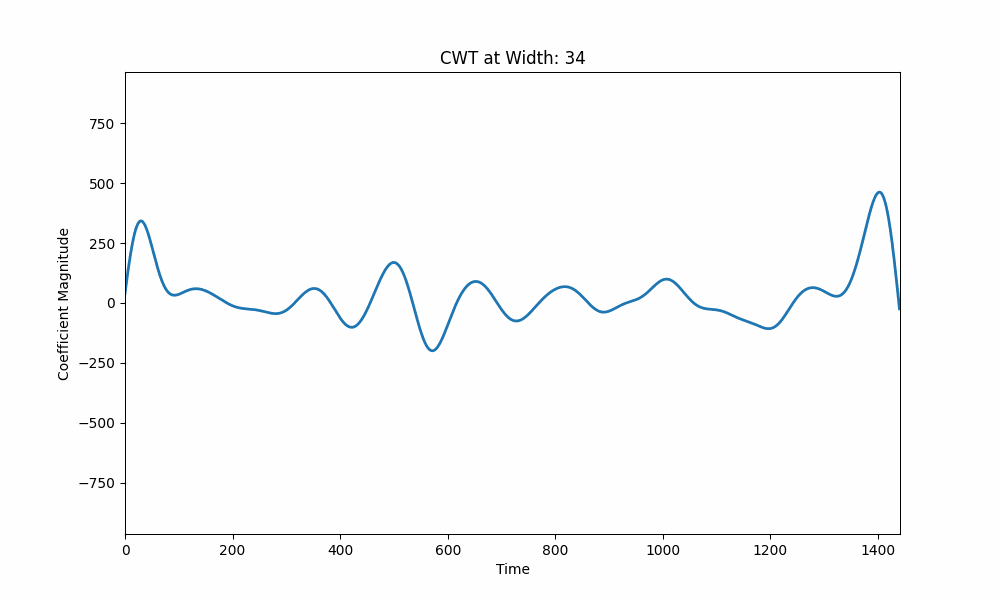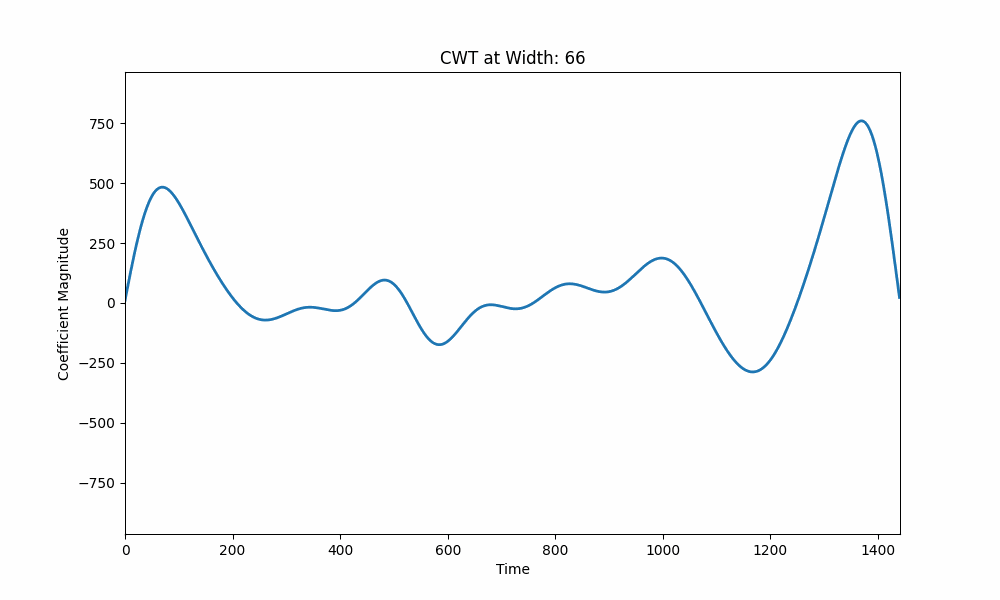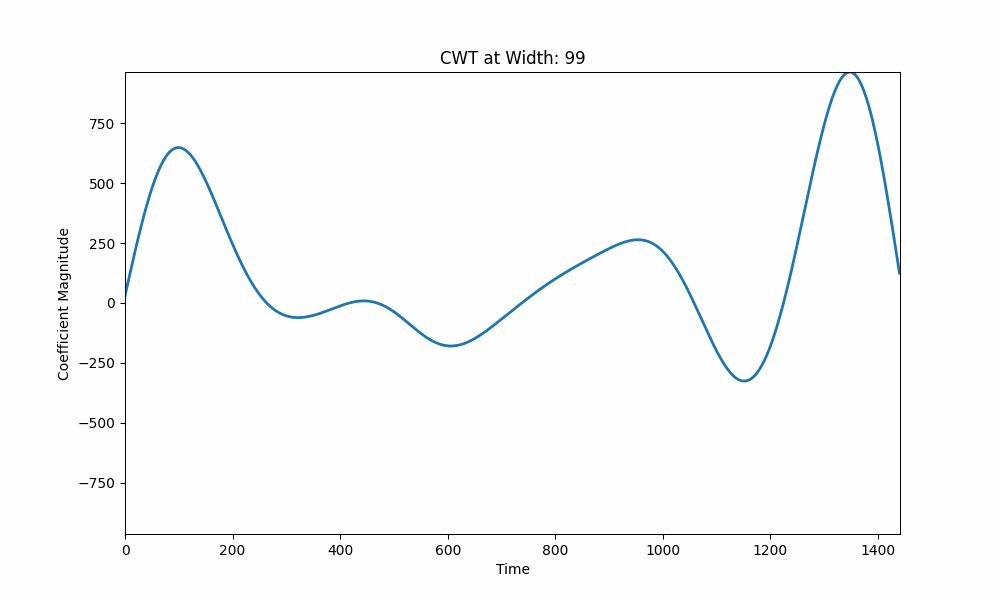
左侧,连续小波变换 (CWT) 以不同的尺度可视化股票数据,捕获不同的持续时间。右侧,Ricker 小波在股票信号中移动,其相关性如下所示。他们共同关注小波如何定位股票数据中的模式,区分短期波动与长期趋势。
在所呈现的可视化中,我们看到小波变换的机制应用于时间序列数据,例如股票价格。在左边,我们看到了连续小波变换(CWT)应用于股票数据的生动写照。动画的每一帧都以不同的比例显示小波系数,捕获不同持续时间存在的模式。较宽的小波检测长期趋势,而较窄的小波则关注短期波动。
在它旁边,右侧是小波(在本例中为 Ricker 小波)如何遍历股票信号的描述。当小波滑动时,它会与股票数据逐点相乘,并将所得值相加以产生单个系数。这种“相关性”如下图所示,其中红点标记了小波移动时的当前系数值。相关图中的高峰值表示小波与股票数据良好对齐的位置,捕获特定模式。从本质上讲,这个过程是一种在大量时间序列数据中挖掘局部模式的系统方法,提供了傅里叶变换可能会错过的精细视角。
3.Python实现
现在,我们将深入研究小波变换的 Python 实现,用于从股票数据中导出买入/卖出信号,这可能是交易者和数据科学家感兴趣的内容。该代码采用连续小波变换来提取可以指示股票历史数据中潜在买入或卖出时刻的特征。
3.1 设置环境
确保您拥有所需的 Python 库。如果没有,可以通过 pip 安装:
pip install numpy pandas matplotlib yfinance scipy
3.2 获取股票数据
使用该yfinance库,我们可以轻松获取股票数据进行分析:
3.3 应用连续小波变换(CWT)
该scipy库提供了使用 Ricker 小波计算 CWT 所需的函数:
import yfinance as yfticker = "SIE.DE"
stock_data = yf.download(ticker, start="2018-01-01", end="2023-12-30")3.4 提取买入和卖出信号
从计算的 CWT 中,可以提取正系数和负系数,分别表示股票价格的向上和向下变动。
from scipy import signalwidths = np.arange(1, 15)
cwt_result = signal.cwt(stock_data['Close'].values, signal.ricker, widths)3.5 识别信号交叉
买入和卖出信号之间的交叉可能预示着交易机会。
cross_above = (buy_signal >= sell_signal) & (buy_signal.shift(1) < sell_signal.shift(1))
cross_below = (buy_signal <= sell_signal) & (buy_signal.shift(1) > sell_signal.shift(1))3.6 可视化
视觉表示可以根据股票的历史数据提供更清晰的买入/卖出时刻的视角:
import matplotlib.pyplot as pltplt.figure(figsize=(30, 6))
plt.plot(stock_data.index, stock_data['Close'], label='Close Prices', alpha=0.5)
plt.scatter(stock_data.index[cross_above], stock_data['Close'][cross_above], label='Buy Signal', marker='^', color='g')
plt.scatter(stock_data.index[cross_below], stock_data['Close'][cross_below], label='Sell Signal', marker='v', color='r')
plt.title(f'{ticker} Historical Close Prices with Wavelet Transform Buy and Sell Signals')
plt.legend()
plt.show()3.7 完整的Python代码
将所有代码放在一起我们得到
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import yfinance as yf
from scipy import signal# Download ASML.AS historical stock data
ticker = "SIE.DE"
stock_data = yf.download(ticker, start="2018-01-01", end="2023-12-30")# Compute the Continuous Wavelet Transform (CWT) using the Ricker wavelet
widths = np.arange(1, 15)
cwt_result = signal.cwt(stock_data['Close'].values, signal.ricker, widths)# Extract the relevant CWT coefficients for analysis
cwt_positive = np.where(cwt_result > 0, cwt_result, 0)
cwt_negative = np.where(cwt_result < 0, cwt_result, 0)# Calculate the buy and sell signals from the CWT coefficients
buy_signal = pd.Series(np.sum(cwt_positive, axis=0), index=stock_data.index)
sell_signal = pd.Series(-np.sum(cwt_negative, axis=0), index=stock_data.index)# Identify buy and sell signal crossovers
cross_above = (buy_signal >= sell_signal) & (buy_signal.shift(1) < sell_signal.shift(1))
cross_below = (buy_signal <= sell_signal) & (buy_signal.shift(1) > sell_signal.shift(1))# Plot the stock prices and buy/sell signals
plt.figure(figsize=(30, 6))
plt.plot(stock_data.index, stock_data['Close'], label='Close Prices', alpha=0.5)
plt.scatter(stock_data.index[cross_above], stock_data['Close'][cross_above], label='Buy Signal', marker='^', color='g')
plt.scatter(stock_data.index[cross_below], stock_data['Close'][cross_below], label='Sell Signal', marker='v', color='r')
plt.title(f'{ticker} Historical Close Prices with Wavelet Transform Buy and Sell Signals')
plt.legend()
plt.show()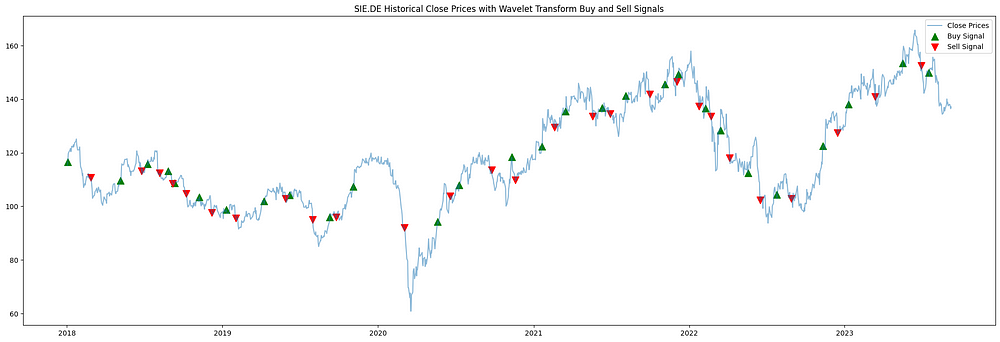
2018 年至 2023 年 SIE.DE 历史收盘价的可视化,使用基本 CWT 方法,使用小波变换衍生的买入(绿色向上三角形)和卖出(红色向下三角形)信号。
3.7 奖励——优化参数
虽然小波变换提供了一种分析股票数据和生成买入/卖出信号的创新方法,但其有效性很大程度上取决于参数的选择:小波的宽度和阈值。这些参数影响我们策略的敏感性和特异性。
使用下面的代码,您可以实施优化技术来系统地选择最佳参数。利用回溯测试功能,我们将模拟各种参数组合的策略过去的表现。最后,我们的目标是微调我们的策略,以最大限度地提高历史业绩,并牢记这句格言:过去的业绩不一定代表未来的结果。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import yfinance as yf
from scipy import signal# Download ASML.AS historical stock data
ticker = "ASML.AS"
stock_data = yf.download(ticker, start="2018-01-01", end="2023-12-30")# Define parameter ranges
widths_range = np.arange(1, 15)
threshold_range = np.arange(0.1, 1.0, 0.1)# Store the best parameters and their performance
best_widths = None
best_threshold = None
best_performance = -np.infdef backtest(stock_data, cross_above, cross_below):# We'll start with one "unit" of cashcash = 1.0 stock = 0.0 position = "out" # Go through each day in our datafor i in range(len(stock_data)):# If we have a buy signal and we're not already holding the stockif cross_above[i] and position == "out":# Buy the stockstock += cash / stock_data['Close'][i]cash = 0.0position = "in"# If we have a sell signal and we're holding the stockelif cross_below[i] and position == "in":# Sell the stockcash += stock * stock_data['Close'][i]stock = 0.0position = "out"# Return our final portfolio valueif position == "in":return cash + stock * stock_data['Close'][-1]else:return cash# Go through each combination of parameters
for widths in widths_range:for threshold in threshold_range:# Compute the CWTcwt_result = signal.cwt(stock_data['Close'].values, signal.ricker, [widths])# Extract relevant coefficientscwt_positive = np.where(cwt_result > threshold, cwt_result, 0)cwt_negative = np.where(cwt_result < -threshold, cwt_result, 0)# Calculate signalsbuy_signal = pd.Series(np.sum(cwt_positive, axis=0), index=stock_data.index)sell_signal = pd.Series(-np.sum(cwt_negative, axis=0), index=stock_data.index)cross_above = (buy_signal >= sell_signal) & (buy_signal.shift(1) < sell_signal.shift(1))cross_below = (buy_signal <= sell_signal) & (buy_signal.shift(1) > sell_signal.shift(1))# Calculate performance based on trading signalsperformance = backtest(stock_data, cross_above, cross_below)# Update best parameters if this performance is betterif performance > best_performance:best_performance = performancebest_widths = widthsbest_threshold = threshold# Print the best parameters
print(f"Best widths: {best_widths}")
print(f"Best threshold: {best_threshold}")
print(f"Best performance: {best_performance * 100}%")# Recalculate the CWT and buy/sell signals using the best parameters
cwt_result = signal.cwt(stock_data['Close'].values, signal.ricker, [best_widths])
cwt_positive = np.where(cwt_result > best_threshold, cwt_result, 0)
cwt_negative = np.where(cwt_result < -best_threshold, cwt_result, 0)
buy_signal = pd.Series(np.sum(cwt_positive, axis=0), index=stock_data.index)
sell_signal = pd.Series(-np.sum(cwt_negative, axis=0), index=stock_data.index)
cross_above = (buy_signal >= sell_signal) & (buy_signal.shift(1) < sell_signal.shift(1))
cross_below = (buy_signal <= sell_signal) & (buy_signal.shift(1) > sell_signal.shift(1))# Plot the stock prices and buy/sell signals
plt.figure(figsize=(30, 6))
plt.plot(stock_data.index, stock_data['Close'], label='Close Prices', alpha=0.5)
plt.scatter(stock_data.index[cross_above], stock_data['Close'][cross_above], label='Buy Signal', marker='^', color='g')
plt.scatter(stock_data.index[cross_below], stock_data['Close'][cross_below], label='Sell Signal', marker='v', color='r')
plt.title(f'{ticker} Historical Close Prices with Wavelet Transform Buy and Sell Signals')
plt.legend()
plt.show()
增强了 ASML.AS 2018 年至 2023 年历史收盘价的可视化,突出显示优化小波变换参数以改善交易性能后获得的买入和卖出信号。
四、解释与分析
对股票数据实施小波变换并使用优化参数对其进行细化后,我们得到了一系列买入和卖出信号。仔细一看:
- 对市场噪音的敏感性:就像其他技术指标一样,小波变换也不能免受市场噪音的影响。然而,其多尺度性质提供了一定程度的弹性,使其能够突出真实模式,同时有可能过滤掉短期波动。
- 周期性模式:股票经常表现出周期性行为——季度财务报告、年度市场趋势等。小波捕获不同规模的此类行为的能力在预测未来走势方面具有显着优势。
- 性能指标:虽然我们的优化提高了历史性能,但必须根据样本外数据验证策略。历史数据的表现并不能保证未来会出现类似的结果。了解潜在的过度拟合至关重要。
5. 潜在的改进和扩展
- 替代小波:我们使用了 Ricker 小波,但其他几个小波系列,例如 Daubechies 或 Haar,可能会提供不同的见解。探索这些可能是一个令人兴奋的途径。
- 合并其他指标:虽然小波变换提供了独特的视角,但将其与其他技术指标相结合可能会加强决策过程。
- 机器学习集成:利用机器学习算法可以帮助更准确地预测买入/卖出信号。小波系数可以作为决策树、神经网络等模型的特征。
- 自适应阈值:适应不断变化的市场条件的动态阈值方法可能会提高信号可靠性,而不是静态阈值。
六,结论
小波变换提供了一个独特的视角来分析股票市场数据,平衡时间和频率的洞察力。虽然它提供了一个全新的视角,但该技术并非万无一失——选择正确的参数至关重要。这种方法只是了解市场走势的众多工具之一。交易者应该将小波分析与其他方法结合起来,以获得更敏锐的洞察力。我们的小波分析之旅强调金融研究的持续创新,始终寻求更清晰的理解和预测能力。