ML | 6 支持向量机

SVM介绍

支持向量机（Support Vector Machines, SVM）是最好的现成的分类器，“现成”指分类器不加修饰可直接使用。

SVM能够对训练集之外的数据点做出很好的分类决策。

SVM其中一种实现方法为序列最小优化（Sequential Minimal Optimization, SMO）算法。

• 优点：泛化错误率低，计算开销不大，结果易解释
• 缺点：对参数调节和核函数的选择敏感，原始分类器不加修改仅适用于处理二类问题。
• 适用数据类型：数值型和标称型数据。

线性不可分数据

如下图所示数据。无法找到一条直线将2组数据分开，这组数据成为线性不可分数据

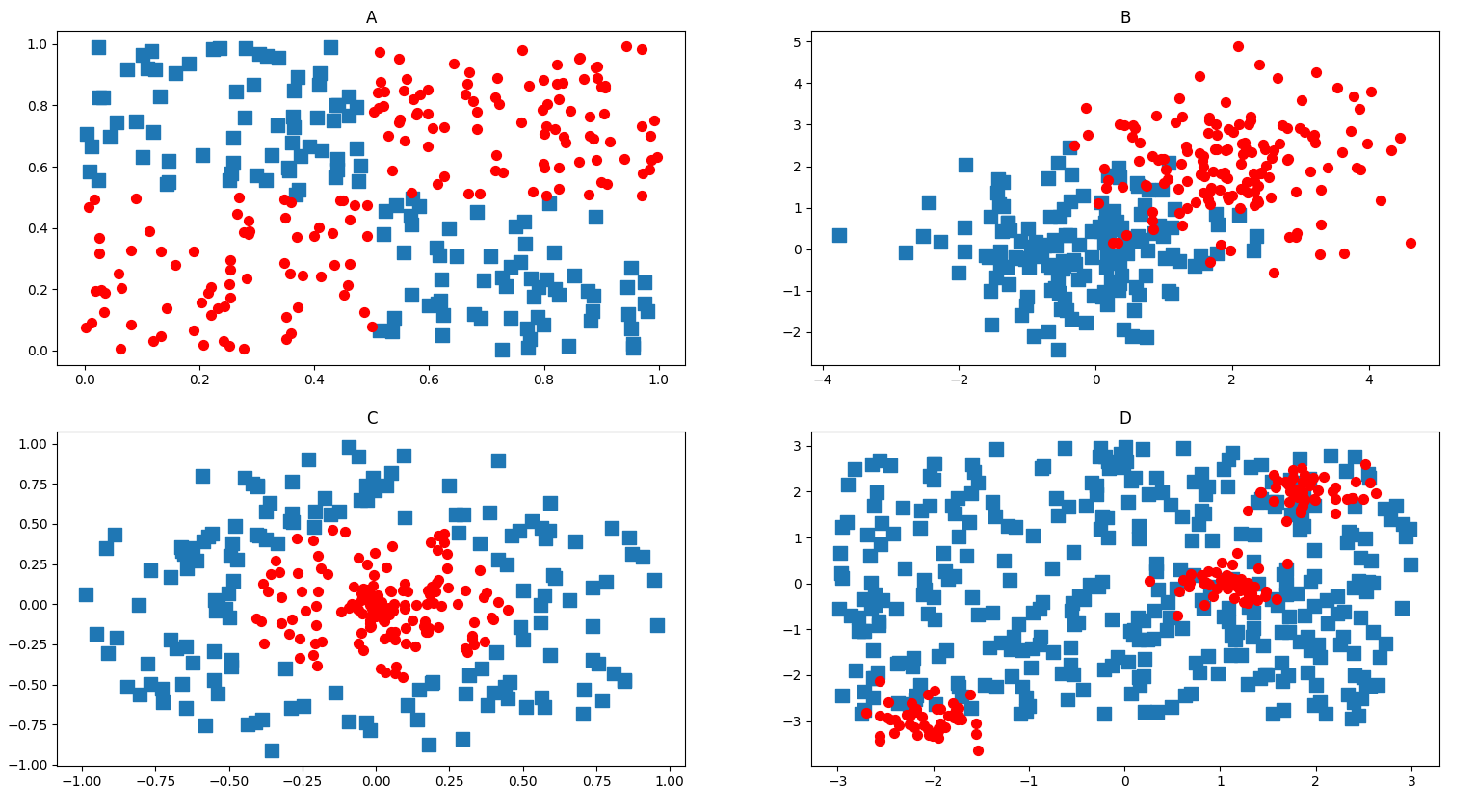
线性可分数据

可以找到一条直线将2组数据点分开

将数据集分隔开来的直线成为分隔超平面，也就是分类的决策边界。

如果数据点离决策边界越远，那么其最后的预测结果也越可信。

支持向量（support vector）就是离分隔超平面最近的那些点。

寻找最大间隔

分隔超平面的形式可以写成 ${\vec{w}}^T\vec{x}+b$

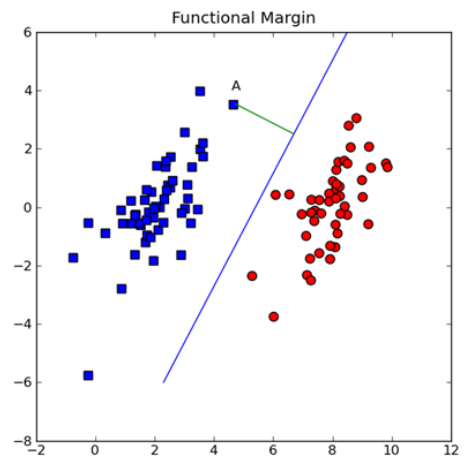
要计算点A到分隔超平面的距离，必须给出点到分隔面的法线或垂线的长度，该值为 $\mid {\vec{w}}^T\vec{x}+b\mid /\mid \mid \vec{w}\mid \mid$，这里的常数b类似于Logistic回归中的截距$w_0$,

这里的向量 w 和常数 b 一起描述了所给数据的分隔线或超平面

分类器求解的优化问题

输入数据给分类器会输出一个类别标签，相当于一个类似于 Sigmoid 的函数在作用

下面使用类似海维赛德阶跃函数（单位阶跃函数）的函数对${\vec{w}}^T\vec{x}+b$作用得到$f({\vec{w}}^T\vec{x}+b)$

其中
$$f(n)=\{\begin{array}{ll}-1,& n<0\\ 1,& n⩾0\end{array}$$
当计算数据点到分隔面的距离并确定分隔面的放置位置时，间隔通过 $label\ast ({\vec{w}}^T\vec{x}+b)$计算

$label\ast (w^{T}x+b)$被称为点到分隔面的函数间隔，$label\ast (w^{T}x+b)\cdot \frac{1}{||\vec{w}||}$称为点到分隔面的几何间隔

现在目标就是找出分类器定义中的 w 和 b，必须找到具有最小间隔的数据点，而这些数据点也就是支持向量。

一旦找到具有最小间隔的数据点，就需要对该间隔最大化
arg ⁡ max ⁡ w , b { min ⁡ n ( l a b e l ⋅ ( w ⃗ T x ⃗ + b ) ) ⋅ 1 ∣ ∣ w ⃗ ∣ ∣ } \arg \max_{w,b}\lbrace \min_n \left( label \cdot \left( \vec{w}^T\vec{x} + b \right) \right) \cdot \frac{1}{\lvert \lvert \vec{w} \rvert \rvert} \rbrace argw,bmax​{nmin​(label⋅(w Tx +b))⋅∣∣w ∣∣1​}
如果令所有支持向量的$ label \cdot \left( \vec{w}^T\vec{x} + b \right) = 1$，那么可以通过求${\lvert \lvert \vec{w} \rvert \rvert}^{-1}$ 的最大值来求最终解。

实际上只有离分隔超平面最近的点得到的值才为1。距离超平面越远的数据点，其$ label \cdot \left( \vec{w}^T\vec{x} + b \right)$值也就越大。

因此这里有一个约束条件$ label \cdot \left( \vec{w}^T\vec{x} + b \right) \geqslant 1.0$。

使用拉格朗日乘子法，目标函数可以写成
$$\underset{\alpha }{\max }\left[{\Sigma }_{i=1}^m\alpha -\frac{1}{2}{\Sigma }_{i,j=1}^{m}labe{l}^{(i)}\cdot labe{l}^{(j)}\cdot {\alpha }_i\cdot {\alpha }_j⟨x^{(i)},x^{(j)}⟩\right]$$
约束条件为：
$$\alpha ⩾0，和{\Sigma }_{i=1}^m{\alpha }_i\cdot labe{l}^{(i)}=0$$

当然实际数据并非那么“干净”，通过引入松弛变量，允许有些数据点可以处于分隔面的错误一侧：
$$C⩾\alpha ⩾0，和{\Sigma }_{i=1}^m{\alpha }_i\cdot labe{l}^{(i)}=0$$
常数C用于控制“最大化间隔”和“保证大部分点的函数间隔小于1.0”这两个目标的权重。

所以，一旦求出了所有的 $\alpha$，分隔超平面就可以通过这些 $\alpha$来表达，而SVM中的主要工作就是求解这些 $\alpha$

SMO高效优化算法

1996年，John Platt 发布了一个成为SMO（Sequential Minimal Optimization）的强大算法，称为序列最小优化，将大优化问题分解为多个小优化问题来求解的。

SMO算法的工作原理是：

每次循环中选择2个$\alpha$ 进行优化处理。

一旦找到一对合适的$\alpha$ ，那么就增大其中1个，同时减小另一个。

“合适”就是要符合条件：

• 2个$\alpha$ 必须要在间隔边界之外
• 2个$\alpha$ 没有进行过区间化处理或者不在边界上

简化版SMO处理小规模数据集

简化版跳过外层循环中确定要优化的最佳$\alpha$ 对，首先在数据集上遍历每一个$\alpha$ ，然后在剩余的$\alpha$ 集合中随机选择另一个$\alpha$ ，从而构成$\alpha$ 对。

同时改变2个$\alpha$ 是因为有一个约束条件：
$${\Sigma }_{i=1}^m{\alpha }_i\cdot labe{l}^{(i)}=0$$
因为总和为0，所以增大1个的同时，必须减少另一个。

伪代码

创建1个 alpha 向量并将其初始化为0向量
当迭代次数小于最大迭代次数时（外循环）：对数据集中每个数据向量（内循环）：如果该数据向量可以被优化：随机选择另外1个数据向量同时优化这2个向量如果2个向量都不能被优化，退出内循环如果所有向量都没有被优化，增加迭代数目，继续下一次循环

程序清单

from numpy import *# 加载数据
def loadDataSet(fileName):dataMat = []; labelMat = []fr = open(fileName)for line in fr.readlines():lineArr = line.strip().split('\t')dataMat.append([float(lineArr[0]), float(lineArr[1])])labelMat.append(float(lineArr[2]))return dataMat,labelMat# 只要函数值不等于输入值i，函数就会进行随机选择
def selectJrand(i,m):j=i #we want to select any J not equal to iwhile (j==i):j = int(random.uniform(0,m))return j# 用于调整大于H或小于L的 alpha 值
def clipAlpha(aj,H,L):if aj > H: aj = Hif L > aj:aj = Lreturn ajdef smoSimple(dataMatIn, classLabels, C, toler, maxIter):dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose() # dataMatrix: 100x2, labelMat:100x1b = 0; m,n = shape(dataMatrix) # m:100, n:2alphas = mat(zeros((m,1)))iter = 0while (iter < maxIter):alphaPairsChanged = 0 # 用于记录 alpha 是否已经经过优化for i in range(m):fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b # 计算预测的类别    Ei = fXi - float(labelMat[i])#if checks if an example violates KKT conditions # =====> alpha 满足条件，误差超限的可以优化 <=====if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)): # 误差很大，对该数据实例所对应的alpha值进行优化j = selectJrand(i,m)fXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + bEj = fXj - float(labelMat[j])alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();# 计算 L和H，low and high，将alpha[j]调整到 0 和 C之间if (labelMat[i] != labelMat[j]):L = max(0, alphas[j] - alphas[i])H = min(C, C + alphas[j] - alphas[i])else:L = max(0, alphas[j] + alphas[i] - C)H = min(C, alphas[j] + alphas[i])if L==H: print("L==H"); continue # L == H 不做修改# Eta是 alpha[j]的最优修改量eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].Tif eta >= 0: print ("eta>=0"); continuealphas[j] -= labelMat[j]*(Ei - Ej)/eta # alphas[j] 减小alphas[j] = clipAlpha(alphas[j],H,L)if (abs(alphas[j] - alphaJold) < 0.00001): print ("j not moving enough"); continue # 检查alpha[j]是否轻微改变，如果是则退出循环，无法优化了# alphas[i] 增大，与 alphas[j] 方向相反alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])#update i by the same amount as j#the update is in the oppostie directionb1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].Tb2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].Tif (0 < alphas[i]) and (C > alphas[i]): b = b1elif (0 < alphas[j]) and (C > alphas[j]): b = b2else: b = (b1 + b2)/2.0alphaPairsChanged += 1print ("iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))if (alphaPairsChanged == 0): iter += 1else: iter = 0print ("iteration number: %d" % iter)return b,alphas

调用函数为：

def main():dataArr, labelArr = loadDataSet('testSet.txt')print("labelArr:\n", labelArr)b, alpha = smoSimple(dataArr, labelArr, 0.6, 0.001, 40)print("b:\n{}".format(b))print("alpha:\n{}".format(alpha[alpha > 0]))for i in range(100):if alpha[i] > 0.0:print(dataArr[i], labelArr[i])

结果：

labelArr:[-1.0, -1.0, 1.0, -1.0, 1.0, 1.0, 1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, 1.0, -1.0, 1.0, 1.0, -1.0, 1.0, -1.0, -1.0, -1.0, 1.0, -1.0, -1.0, 1.0, 1.0, -1.0, -1.0, -1.0, -1.0, 1.0, 1.0, 1.0, 1.0, -1.0, 1.0, -1.0, -1.0, 1.0, -1.0, -1.0, -1.0, -1.0, 1.0, 1.0, 1.0, 1.0, 1.0, -1.0, 1.0, 1.0, -1.0, -1.0, 1.0, 1.0, -1.0, 1.0, -1.0, -1.0, -1.0, -1.0, 1.0, -1.0, 1.0, -1.0, -1.0, 1.0, 1.0, 1.0, -1.0, 1.0, 1.0, -1.0, -1.0, 1.0, -1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, -1.0, -1.0, -1.0, -1.0, 1.0, -1.0, 1.0, 1.0, 1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0]L==H
L==H
...
iter: 0 i:19, pairs changed 4
L==H
L==H
j not moving enough
j not moving enough
j not moving enough
iter: 0 i:29, pairs changed 5
...
j not moving enough
iteration number: 39
j not moving enough
j not moving enough
j not moving enough
iteration number: 40b:
[[-3.81491092]]
alpha:
[[0.13641633 0.21141175 0.02064304 0.36847111]][4.658191, 3.507396] -1.0
[3.457096, -0.082216] -1.0
[2.893743, -1.643468] -1.0
[6.080573, 0.418886] 1.0

完整Platt SMO 算法加速优化

Platt SMO 算法是通过1个外循环来选择第1个$\alpha$ 值的，并且其选择过程会在2种方式之间交替:

• 在所有数据集上进行单遍扫描

• 在非边界$\alpha$中实现单遍扫描。非边界$\alpha$指不等于边界0或C的$\alpha$值

  实现非边界$\alpha$值扫描时，首先需要建立这些$\alpha$值的列表，然后再对这个表进行遍历。同时跳过那些已知不会改变的$\alpha$值

在选择第1个$\alpha$值后，算法会通过1个内循环来选择第2个$\alpha$值，会通过最大化步长的方式获得第2个$\alpha$值

完整 Platt SMO的支持函数

class optStruct:# 初始化函数，完成成员变量的填充def __init__(self,dataMatIn, classLabels, C, toler, kTup):  # Initialize the structure with the parameters self.X = dataMatInself.labelMat = classLabelsself.C = Cself.tol = tolerself.m = shape(dataMatIn)[0]self.alphas = mat(zeros((self.m,1)))self.b = 0self.eCache = mat(zeros((self.m,2))) #first column is valid flag，seccond column is E valueself.K = mat(zeros((self.m,self.m)))for i in range(self.m):self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)# 计算E值
def calcEk(oS, k):fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)Ek = fXk - float(oS.labelMat[k])return Ek# 选择第2个 alpha/ 内循环的alpha值
def selectJ(i, oS, Ei):         #this is the second choice -heurstic, and calcs EjmaxK = -1; maxDeltaE = 0; Ej = 0oS.eCache[i] = [1,Ei]  #set valid #choose the alpha that gives the maximum delta EvalidEcacheList = nonzero(oS.eCache[:,0].A)[0] # 构建了1个非0表，返回非0 E值所对应的alpha值的数组序号，而不是E值本身if (len(validEcacheList)) > 1:for k in validEcacheList:   #loop through valid Ecache values and find the one that maximizes delta Eif k == i: continue #don't calc for i, waste of timej not moving enoughdeltaE = abs(Ei - Ek)if (deltaE > maxDeltaE):maxK = k; maxDeltaE = deltaE; Ej = Ekreturn maxK, Ejelse:   #in this case (first time around) we don't have any valid eCache valuesj = selectJrand(i, oS.m)Ej = calcEk(oS, j)return j, Ejdef updateEk(oS, k):#after any alpha has changed update the new value in the cacheEk = calcEk(oS, k)oS.eCache[k] = [1,Ek]

新建了1个数据结构来保存所有的重要值——optStruct，使得数据可以通过1个对象进行传递。

完整Platt SMO算法中的优化例程

def innerL(i, oS):Ei = calcEk(oS, i)if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrandalphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();if (oS.labelMat[i] != oS.labelMat[j]):L = max(0, oS.alphas[j] - oS.alphas[i])H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])else:L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)H = min(oS.C, oS.alphas[j] + oS.alphas[i])if L==H: print ("L==H"); return 0eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #changed for kernelif eta >= 0: print ("eta>=0"); return 0oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/etaoS.alphas[j] = clipAlpha(oS.alphas[j],H,L)updateEk(oS, j) #added this for the Ecacheif (abs(oS.alphas[j] - alphaJold) < 0.00001): print ("j not moving enough"); return 0oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as jupdateEk(oS, i) #added this for the Ecache                    #the update is in the oppostie directionb1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2else: oS.b = (b1 + b2)/2.0return 1else: return 0

这里代码与smoSimple中代码一致，使用了自定义的数据结构。

函数使用selectJ而不是selectJrand（）来选择第2个alpha值。在alpha值改变时更新Ecache。

完整Platt SMO 的外循环代码

def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)):    #full Platt SMOoS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)iter = 0entireSet = True; alphaPairsChanged = 0while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):alphaPairsChanged = 0if entireSet:   #go over allfor i in range(oS.m):        alphaPairsChanged += innerL(i,oS)print ("fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))iter += 1else:#go over non-bound (railed) alphasnonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]for i in nonBoundIs:alphaPairsChanged += innerL(i,oS)print ("non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))iter += 1if entireSet: entireSet = False #toggle entire set loopelif (alphaPairsChanged == 0): entireSet = True  print ("iteration number: %d" % iter)return oS.b,oS.alphas

整个代码主体是while循环。当迭代次数超过指定的最大值，或者遍历整个集合都未对任意$\alpha$ 对进行修改时，就退出循环。

maxIter变量作用：

• smoSimple(): 当没有任何$\alpha$发生改变时会将整个集合的1次遍历过程计成1次迭代
• smoP(): 1次迭代定义为1次循环过程，如果优化过程中存在波动就会停止。

调用函数

dataArr, labelArr = loadDataSet('testSet.txt')
b, alpha = smoP(dataArr, labelArr, 0.6, 0.001, 40)
print("b:\n{}".format(b))
print("alpha:\n{}".format(alpha[alpha > 0]))

结果：

j not moving enough
fullSet, iter: 3 i:76, pairs changed 0
fullSet, iter: 3 i:77, pairs changed 0
fullSet, iter: 3 i:78, pairs changed 0
fullSet, iter: 3 i:79, pairs changed 0
fullSet, iter: 3 i:80, pairs changed 0
fullSet, iter: 3 i:81, pairs changed 0
fullSet, iter: 3 i:82, pairs changed 0
fullSet, iter: 3 i:83, pairs changed 0
fullSet, iter: 3 i:84, pairs changed 0
fullSet, iter: 3 i:85, pairs changed 0
fullSet, iter: 3 i:86, pairs changed 0
fullSet, iter: 3 i:87, pairs changed 0
fullSet, iter: 3 i:88, pairs changed 0
fullSet, iter: 3 i:89, pairs changed 0
fullSet, iter: 3 i:90, pairs changed 0
fullSet, iter: 3 i:91, pairs changed 0
fullSet, iter: 3 i:92, pairs changed 0
fullSet, iter: 3 i:93, pairs changed 0
j not moving enough
fullSet, iter: 3 i:94, pairs changed 0
fullSet, iter: 3 i:95, pairs changed 0
fullSet, iter: 3 i:96, pairs changed 0
j not moving enough
fullSet, iter: 3 i:97, pairs changed 0
fullSet, iter: 3 i:98, pairs changed 0
fullSet, iter: 3 i:99, pairs changed 0
iteration number: 4
b:
[[-2.70721904]]
alpha:
[[0.12020075 0.0709378  0.0119673  0.0119673  0.01213881 0.021545790.02154579 0.06140175]]Process finished with exit code 0

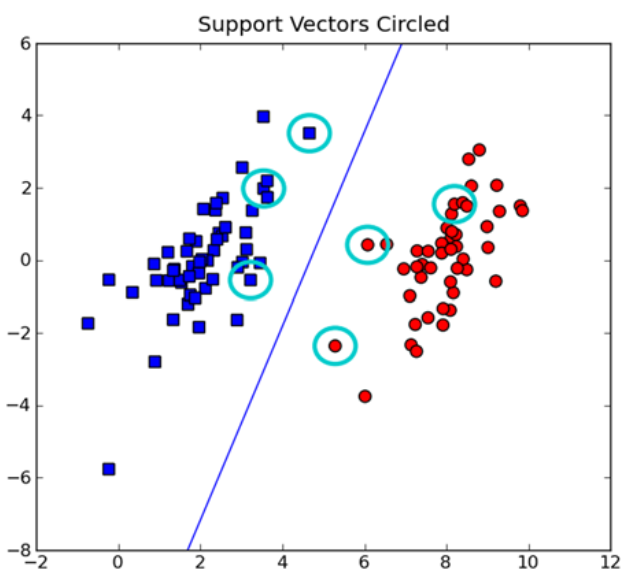
分类

上面花了很多时间计算$\alpha$值，如何利用它们进行分类呢？

首先基于$\alpha$值得到超平面，包括w的计算

def calcWs(alphas,dataArr,classLabels):X = mat(dataArr); labelMat = mat(classLabels).transpose()m,n = shape(X)w = zeros((n,1))for i in range(m):w += multiply(alphas[i]*labelMat[i],X[i,:].T)return w

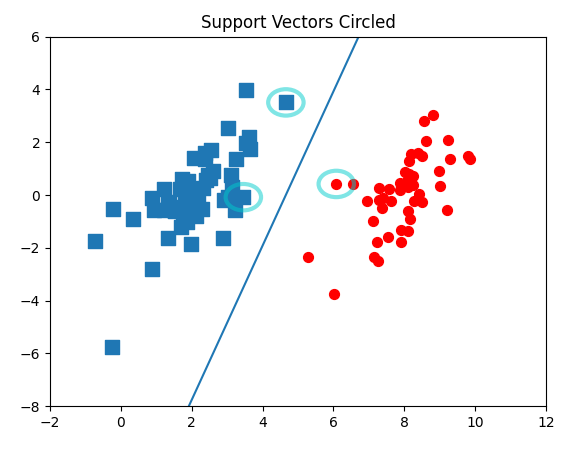
这里非0 $\alpha$所对应的也就是支持向量。

计算上述 smoP的权重

ws = calcWs(alpha, dataArr, labelArr)
print("ws:\n", ws)ws:[[ 0.74502787][-0.18148056]]

根据公式 $ dataMat * ws +b$ 的结果判断数据分类，结果大于0，则属于1类，结果小于0，则属于-1类。

在复杂数据上应用核函数

考虑上图给出的数据，数据点分布在一个圆的内部和外部。这个数据在2维平面中很难用一条直线分隔。

需要使用核函数（kernel）的工具将数据转换成易于分类器理解的形式。

可行的办法，就是将数据从一个特征空间转换到另一个特征空间，这种映射，通常情况下，会将低维特征空间映射到高维空间。

径向基核函数

径向基核函数是SVM中常用的一个核函数。

径向基函数是一个采用向量作为自变量的函数，能够基于向量距离运算输出一个标量。

径向基函数的高斯版本为：
$$k(x,y)=\exp \left(\frac{-\mid \mid x-y\mid {\mid }^2}{2{\sigma }^2}\right)$$
其中，$\sigma$是用户定义的用于确定到达率（reach）或者说函数值跌落到0的速度参数。

可以写一个核转换函数，其中使用核函数

def kernelTrans(X, A, kTup): #calc the kernel or transform data to a higher dimensional spacem,n = shape(X)K = mat(zeros((m,1)))if kTup[0]=='lin': K = X * A.T   #linear kernelelif kTup[0]=='rbf':for j in range(m):deltaRow = X[j,:] - AK[j] = deltaRow*deltaRow.TK = exp(K/(-1*kTup[1]**2)) #divide in NumPy is element-wise not matrix like Matlabelse: raise NameError('Houston We Have a Problem -- \That Kernel is not recognized')return Kclass optStruct:def __init__(self,dataMatIn, classLabels, C, toler, kTup):  # Initialize the structure with the parameters self.X = dataMatInself.labelMat = classLabelsself.C = Cself.tol = tolerself.m = shape(dataMatIn)[0]self.alphas = mat(zeros((self.m,1)))self.b = 0self.eCache = mat(zeros((self.m,2))) #first column is valid flagself.K = mat(zeros((self.m,self.m)))for i in range(self.m):self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)

kTup 是一个包含核函数信息的元祖。

测试中使用核函数

构建1个对非线性数据点进行有效分类的分类器，该分类器使用了径向基核函数。

def testRbf(k1=1.3):dataArr,labelArr = loadDataSet('testSetRBF.txt')b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1)) #C=200 importantdatMat=mat(dataArr); labelMat = mat(labelArr).transpose()svInd=nonzero(alphas.A>0)[0]sVs=datMat[svInd] #get matrix of only support vectorslabelSV = labelMat[svInd];print ("there are %d Support Vectors" % shape(sVs)[0])m,n = shape(datMat)errorCount = 0for i in range(m):# 利用核函数进行分类kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b # 利用支持向量数据进行分类if sign(predict)!=sign(labelArr[i]): errorCount += 1print ("the training error rate is: %f" % (float(errorCount)/m))dataArr,labelArr = loadDataSet('testSetRBF2.txt')errorCount = 0datMat=mat(dataArr); labelMat = mat(labelArr).transpose()m,n = shape(datMat)for i in range(m):kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + bif sign(predict)!=sign(labelArr[i]): errorCount += 1    print ("the test error rate is: %f" % (float(errorCount)/m))

整个代码最重要的是for循环开始的那2行，它们给出了如何利用核函数进行分类。

结果：

...
L==H
fullSet, iter: 4 i:91, pairs changed 0
L==H
fullSet, iter: 4 i:92, pairs changed 0
fullSet, iter: 4 i:93, pairs changed 0
fullSet, iter: 4 i:94, pairs changed 0
fullSet, iter: 4 i:95, pairs changed 0
fullSet, iter: 4 i:96, pairs changed 0
fullSet, iter: 4 i:97, pairs changed 0
fullSet, iter: 4 i:98, pairs changed 0
fullSet, iter: 4 i:99, pairs changed 0
iteration number: 5
there are 25 Support Vectors
the training error rate is: 0.080000
the test error rate is: 0.110000Process finished with exit code 0

当然可以尝试更换不同的k1参数以观察错误率、训练错误率、支持向量个数随k1的变化情况。

支持向量的数目存在一个最优值。

SVM的优点在于能够对数据进行高效分类。

如果支持向量太少，可能会得到一个很差的决策边界；如果支持向量太多，相当于每次都利用整个数据集进行分类，这种分类方法称为k-近邻

手写识别问题回顾

使用第2章中的一些代码和SMO算法，可以构建1个系统测试手写数字的分类器。

def img2vector(filename):returnVect = zeros((1,1024))fr = open(filename)for i in range(32):lineStr = fr.readline()for j in range(32):returnVect[0,32*i+j] = int(lineStr[j])return returnVectdef loadImages(dirName):from os import listdirhwLabels = []trainingFileList = listdir(dirName)           #load the training setm = len(trainingFileList)trainingMat = zeros((m,1024))for i in range(m):fileNameStr = trainingFileList[i]fileStr = fileNameStr.split('.')[0]     #take off .txtclassNumStr = int(fileStr.split('_')[0])if classNumStr == 9: hwLabels.append(-1)else: hwLabels.append(1)trainingMat[i,:] = img2vector('%s/%s' % (dirName, fileNameStr))return trainingMat, hwLabels    def testDigits(kTup=('rbf', 10)):dataArr,labelArr = loadImages('trainingDigits')b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, kTup)datMat=mat(dataArr); labelMat = mat(labelArr).transpose()svInd=nonzero(alphas.A>0)[0]sVs=datMat[svInd] labelSV = labelMat[svInd];print("there are %d Support Vectors" % shape(sVs)[0])m,n = shape(datMat)errorCount = 0for i in range(m):kernelEval = kernelTrans(sVs,datMat[i,:],kTup)predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + bif sign(predict)!=sign(labelArr[i]): errorCount += 1print ("the training error rate is: %f" % (float(errorCount)/m))dataArr,labelArr = loadImages('testDigits')errorCount = 0datMat=mat(dataArr); labelMat = mat(labelArr).transpose()m,n = shape(datMat)for i in range(m):kernelEval = kernelTrans(sVs,datMat[i,:],kTup)predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + bif sign(predict)!=sign(labelArr[i]): errorCount += 1    print ("the test error rate is: %f" % (float(errorCount)/m) )

测试testDigits(('rbf',20)，得结果：

....
fullSet, iter: 2 i:394, pairs changed 0
fullSet, iter: 2 i:395, pairs changed 0
fullSet, iter: 2 i:396, pairs changed 0
fullSet, iter: 2 i:397, pairs changed 0
L==H
fullSet, iter: 2 i:398, pairs changed 0
fullSet, iter: 2 i:399, pairs changed 0
fullSet, iter: 2 i:400, pairs changed 0
fullSet, iter: 2 i:401, pairs changed 0
iteration number: 3
there are 61 Support Vectors
the training error rate is: 0.002488
the test error rate is: 0.010753

---

欢迎关注公众号【三戒纪元】