0/1背包问题理论基础

二维dp数组

动规五部曲

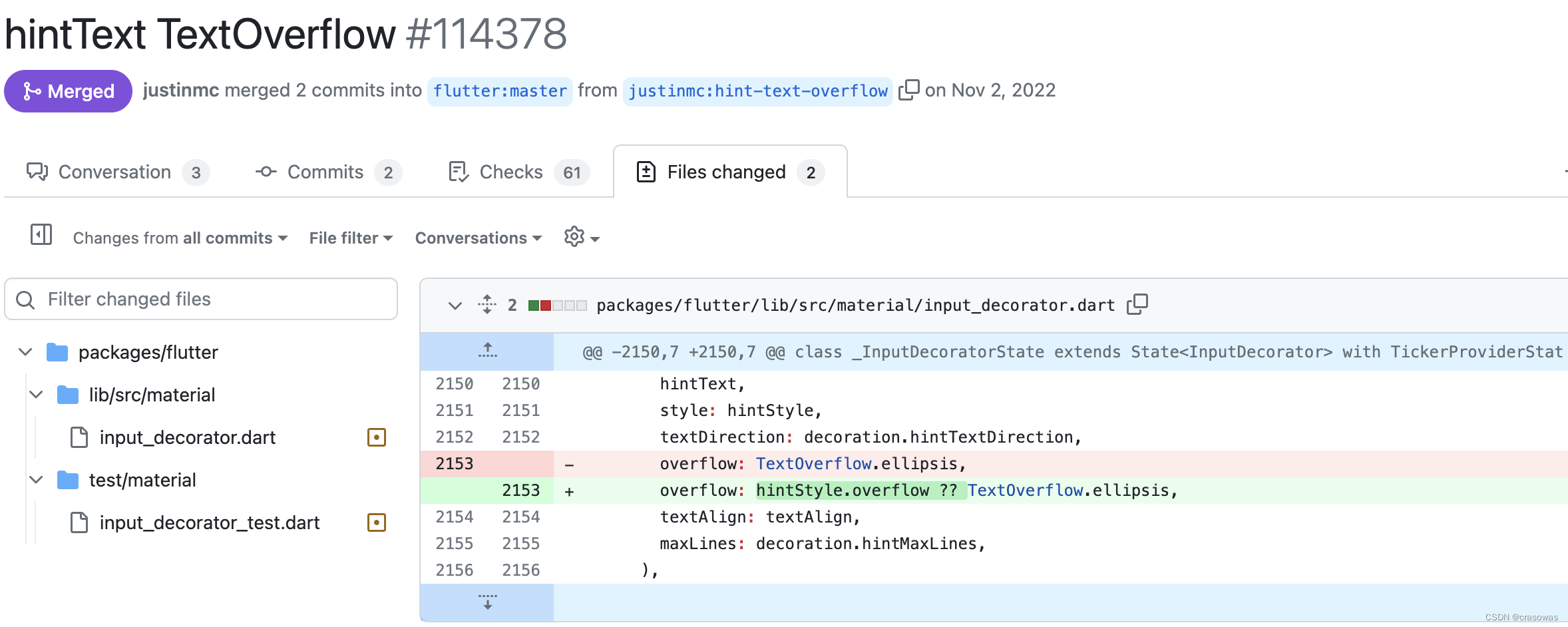
1.确定dp数组及下标含义: dp[i][j] : 从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和的最大值；

2.确定递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])；

3.dp数组如何初始化：

vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];
}

4.确定遍历顺序：物品遍历的for循环放在外层，遍历背包的for循环放在内层；

5.举例递推dp数组

测试代码：

void test1() {vector<int> weight = {1, 3, 4};vector<int> value = {15, 20, 30};int bagweight = 4;vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];}for (int i = 1; i < weight.size(); i++) {for (int j = 0; j <= bagweight; j++) {if (j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - wight[i]] + value[i]);}}cout << dp[weight.size() - 1][bagweight] << endl;
}
int main() {test1();
}

一维dp数组

动规五部曲

1.确定dp数组及下标含义: dp[j] : 容量为j的背包，所背的物品价值最大值；

2.确定递推公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

3.dp数组如何初始化：dp[0] = 0;

4.确定遍历顺序：物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历;

for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}

5.举例递推dp数组

测试代码：

void test2() {vector<int> weight = {1, 3, 4};vector<int> value = {15, 20, 30};int bagweight = 4;vector<int> dp(bagweight + 1, 0);for (int i = 0; i < weight.size(); i++) {for (int j = bagweight; j >= weight[i]; j--) {dp[j] = max(dp[i], dp[j - weight[i]] + value[i]);}}cout << dp[bagweight] << endl;
}
int main() {test2();
}

LeeCode 416. 分割等和子集

416. 分割等和子集 - 力扣（LeetCode）

思路：

1.确定dp数组及下标含义: dp[j] : 容量为j的背包，所背的物品价值最大值；

2.确定递推公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

3.dp数组如何初始化：dp[0] = 0;

4.确定遍历顺序：物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历;

5.举例递推dp数组

代码：

class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0;vector<int> dp(10001, 0);for (int i = 0; i < nums.size(); i++) {sum += nums[i];} if (sum % 2 == 1) return false;int target = sum / 2;for (int i = 0; i < nums.size(); i++) {for (int j = target; j >= nums[i]; j--) {dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);}}if (dp[target] == target) return true;return false;}
};

时间复杂度：O（n²）空间复杂度：O(n)