0 Floyd算法介绍
- 和 Dijkstra 算法一样,弗洛伊德(Floyd)算法也是一种用于寻找给定的加权图中顶点间最短路径的算法。该算法名称以创始人之一、1978 年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名
- 弗洛伊德算法(Floyd)计算图中各个顶点之间的最短路径
- 迪杰斯特拉算法用于计算图中某一个顶点到其他顶点的最短路径。
- 弗洛伊德算法 VS 迪杰斯特拉算法:迪杰斯特拉算法通过选定的被访问顶点,求出从出发访问顶点到其他顶点的最短路径;弗洛伊德算法中每一个顶点都是出发访问点,所以需要将每一个顶点看做被访问顶点,求出从每一个顶点到其他顶点的最短路径。
- 回顾:迪杰斯特拉算法
1 Floyd算法应用
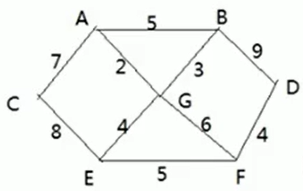
最短路径问题:
- 胜利乡有 7 个村庄(A, B, C, D, E, F, G)
- 各个村庄的距离用边线表示(权) ,比如 A – B 距离 5 公里
- 问:如何计算出各村庄到 其它各村庄的最短距离?
思路分析:
- 核心思想:穷举
- 三层for循环分别使3个指针指向三个顶点,最外层表示中间顶点k
- k=0则表示A顶点作为中间顶点,那么就可以更新BC和CG间的最短路径
- k从0->6,则可以得到所有顶点间的最短路径
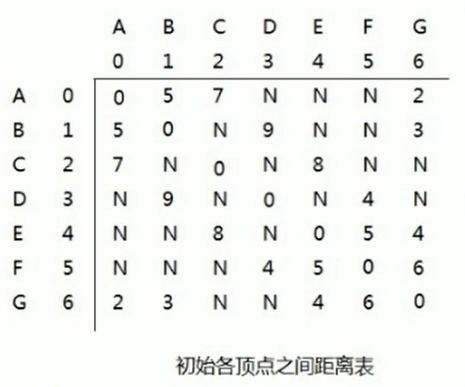
- 当然想法简单,但是实现起来需要借助辅助变量,这里用到初始值为邻接矩阵的距离表dis和初始值为出发点的前驱关系表pre

个人理解:
-
为什么如此初始化前驱关系表?
因为默认开始只有两种路线:直连/不直连,两种情况下默认前驱节点都是出发点,即出发点到任何顶点的前驱节点都是自己,至于后续的改动,不管最短路线改为非直连的两段还是三段,也只是针对不直连的路(即65535),而直连的两个顶点相关数据无需改动,前驱自然就是终点的前驱节点,即出发点
-
两顶点之间非直连,最短路径为3段的,最短路径是怎么更新的,如CD的最短路径为CEFD?
观察:虽然F作为中间点,但是测试时中间点第一个就用F,CD的距离和前驱都未能更新,仅更新了DE之间和DG之间数据,而当F之后的E作为中间点,CD之间数据才能更新,即CD的前驱为F,为什么会如此?
注意:这是因为F作为中间点时,CEFD中存在65535,即CF间距此时还是65535所以CD无法更新,而E作为中间点时之前更新了ED=EF+FD,所以CD=CE+ED,CD相关数据才得以更新
结论:当MN两点之间最短路径需要经过n个顶点,那么只有当这n个中间点的相关数据全部更完,MN间的数据才能更新,也可以说,想更新MN的数据,必须保证路径上没有65535
//弗洛伊德算法:最短路径问题
public class FloydAlgorithm {public static void main(String[] args) {//测试看看图是否创建成功char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };//创建邻接矩阵int[][] matrix = new int[vertex.length][vertex.length];final int N = 65535;matrix[0] = new int[] { 0, 5, 7, N, N, N, 2 };matrix[1] = new int[] { 5, 0, N, 9, N, N, 3 };matrix[2] = new int[] { 7, N, 0, N, 8, N, N };matrix[3] = new int[] { N, 9, N, 0, N, 4, N };matrix[4] = new int[] { N, N, 8, N, 0, 5, 4 };matrix[5] = new int[] { N, N, N, 4, 5, 0, 6 };matrix[6] = new int[] { 2, 3, N, N, 4, 6, 0 };Graph graph = new Graph(vertex, matrix);graph.floyd();graph.show();}
}class Graph {private char[] vertex;private int[][] dis;private int[][] pre;public Graph(char[] vertex, int[][] matrix) {this.vertex = vertex;//初始化最短路径数组为邻接矩阵,直连就是最短路径,非直连则需要找this.dis = matrix;pre = new int[vertex.length][vertex.length];for (int i = 0; i < pre.length; i++) {//这里为什么如此初始化前驱节点?//答:因为默认开始只有两种路线:直连/不直连,两种情况下默认前驱节点都是出发点,即出发点到任何顶点的前驱节点都是自己// 至于后续的改动,不管最短路线改为非直连的两段还是三段,也只是针对不直连的路(即65535),// 而直连的两个顶点相关数据无需改动,前驱自然就是终点的前驱节点,即出发点Arrays.fill(pre[i], i);}}public void show() {for (int i = 0; i < vertex.length; i++) {for (int p : pre[i]) {System.out.print(vertex[p]+" ");}System.out.println();for (int j = 0; j < vertex.length; j++) {System.out.print("["+vertex[i]+"->"+vertex[j]+"="+dis[i][j]+"] ");}System.out.println("\n");}}public void floyd() {int len = 0;//问题:两顶点之间非直连,最短路径为3段的,最短路径是怎么更新的,如CD的最短路径为CEFD?//答:// 观察:虽然F作为中间点,但是测试时中间点第一个就用F,CD的距离和前驱都未能更新,仅更新了DE之间和DG之间数据,// 而当F之后的E作为中间点,CD之间数据才能更新,即CD的前驱为F,为什么会如此?// 注意:这是因为F作为中间点时,CEFD中存在65535,即CF间距此时还是65535所以CD无法更新,而E作为中间点时之前更新了ED=EF+FD// 所以CD=CE+ED,CD相关数据才得以更新// 结论:当MN两点之间最短路径需要经过n个顶点,那么只有当这n个中间点的相关数据全部更完,MN间的数据才能更新// 也可以说,想更新MN的数据,必须保证路径上没有65535int[] range = {5,4,3,2,1,0,6};for (int k : range) {//BC CGSystem.out.println(vertex[k] + "作为中间节点");for (int i = 0; i < vertex.length; i++) {for (int j = 0; j < vertex.length; j++) {len = dis[i][k] + dis[k][j];if (len < dis[i][j]) {System.out.println("修改了:[" + vertex[i] + "-" + vertex[j] + "]");dis[i][j] = len;//直连的前驱(出发点)改为非直连后半段(最后一段)的前驱(出发点)//举例:AE>AG+GE,所以A(pre[AE])=G(pre[GE])pre[i][j] = pre[k][j];}}}}}
}