文章目录
- 🍀排序的概念及引用
- 🐱👤排序的概念
- 🐱👓排序运用
- 🐱🐉常见的排序算法
- 🌴插入排序
- 🎋基本思想:
- 🛫直接插入排序
- 📌算法步骤:
- 📌代码实现:
- 📌直接插入排序特性:
- 🛬希尔排序( 缩小增量排序 )
- 📌算法步骤:
- 📌代码实现:
- 📌希尔排序的特性总结
- 🌳选择排序
- 🎋基本思想
- 🛫直接选择排序
- 🚩 算法步骤:
- 🚩代码实现:
- 🚩直接选择排序的特性总结
- 🎄堆排序
- 🚩算法步骤
- 🚩代码实现:
- 🚩堆排序的特性总结
- ⭕总结
🍀排序的概念及引用
🐱👤排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。

内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序
🐱👓排序运用
比如我们在逛淘宝时
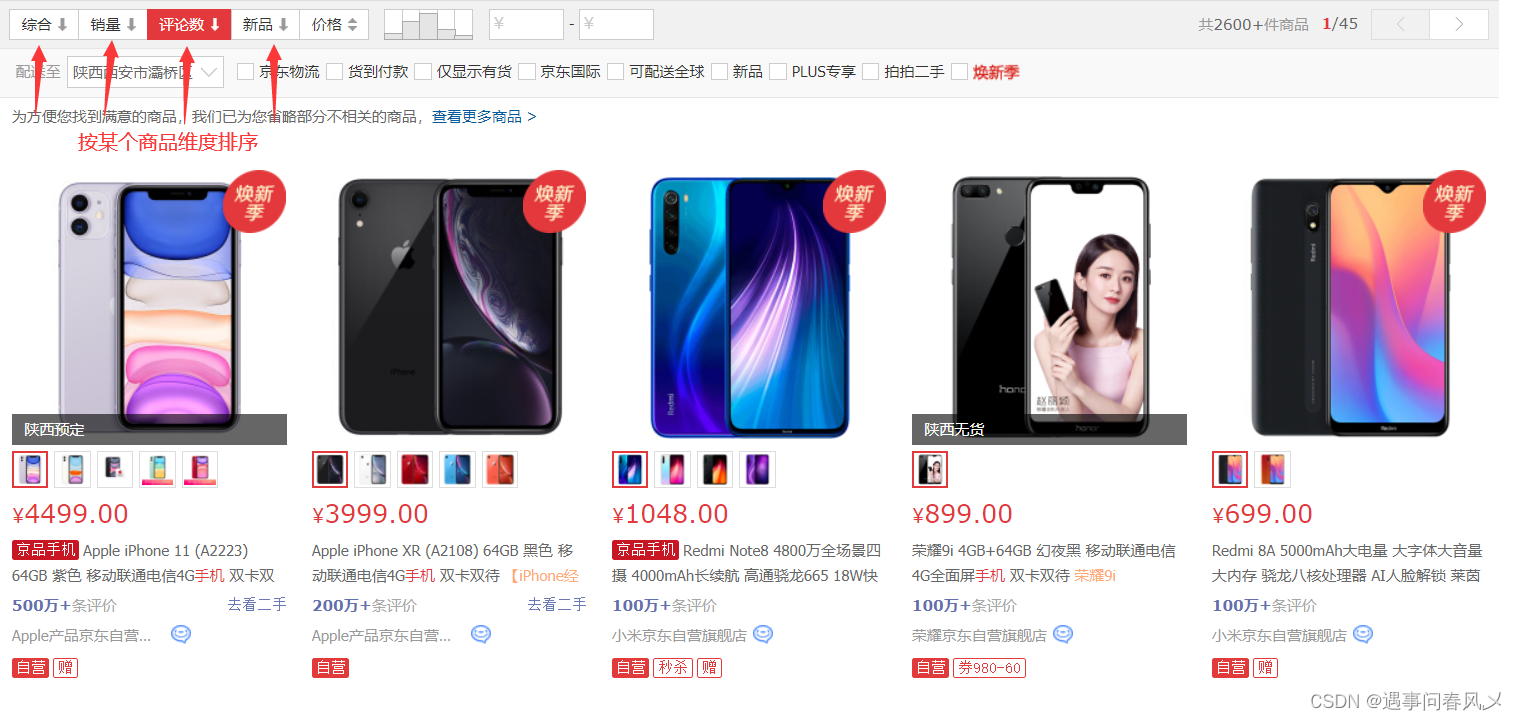
🐱🐉常见的排序算法
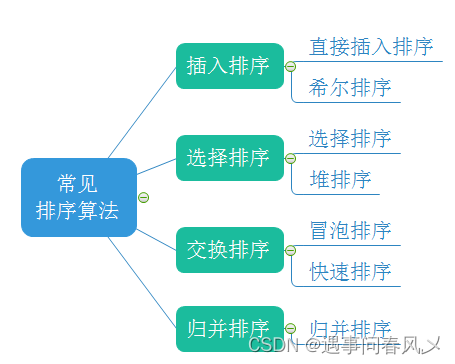
本篇博客将着重讲解前四种算法
🌴插入排序
🎋基本思想:
直接插入排序是一种简单的插入排序法,其基本思想是:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
实际中我们玩扑克牌时,就用了插入排序的思想。

🛫直接插入排序
插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴,但它的原理应该是最容易理解的了,因为只要打过扑克牌的人都应该能够秒懂。
插入排序是一种最简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
插入排序和冒泡排序一样,也有一种优化算法,叫做拆半插入。
📌算法步骤:
将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)

即当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移
📌代码实现:
public void straightInsertion(int[] array) {int len = array.length;for(int i = 1; i < len ; i++) {int count = array[i];int j = i - 1;for( ; j >= 0; j --) {if(count < array[j]) {array[j + 1] = array[j];} else {break;}}array[j + 1] = count;}}
📌直接插入排序特性:
-
元素集合越接近有序,直接插入排序算法的时间效率越高
-
时间复杂度:O(N^2)
-
空间复杂度:O(1),它是一种稳定的排序算法
-
稳定性:稳定
🛬希尔排序( 缩小增量排序 )
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率;
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位;
希尔排序的基本思想是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序
📌算法步骤:
选择一个增量序列 t1,t2,……,tk,其中 ti > tj, tk = 1;
按增量序列个数 k,对序列进行 k 趟排序;
每趟排序,根据对应的增量 gap,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。

动图演示如下:

📌代码实现:
public void straightInsertion(int[] array,int gap) {int len = array.length;for(int i = gap; i < len ; i++) {int count = array[i];int j = i - gap;for( ; j >= 0; j-=gap) {if(count < array[j]) {array[j + gap] = array[j];} else {break;}}array[j + gap] = count;}}public void shellSort(int[] arrary) {int gap = arrary.length;while(gap > 0) {gap = gap /2;straightInsertion(arrary,gap);}}📌希尔排序的特性总结
-
希尔排序是对直接插入排序的优化。
-
当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
-
希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的希尔排序的时间复杂度都不固定,以下来自大佬的给出的解释
《数据结构(C语言版)》— 严蔚敏

《数据结构-用面向对象方法与C++描述》— 殷人昆

- 稳定性:不稳定
🌳选择排序
🎋基本思想
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
🛫直接选择排序
选择排序是一种简单直观的排序算法,无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。
🚩 算法步骤:
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
重复第二步,直到所有元素均排序完毕。
即:
-
在元素集合array[i]–array[n-1]中选择关键码最大(小)的数据元素
-
若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换
-
在剩余的array[i]–array[n-2](array[i+1]–array[n-1])集合中,重复上述步骤,直到集合剩余1个元素

🚩代码实现:
public static void selectSort(int[] array) {for (int i = 0; i < array.length; i++) {int minIndex = i;int j = i+1;for (; j < array.length; j++) {if(array[j] < array[minIndex]) {minIndex = j;}}swap(array,i,minIndex);}}private static void swap(int[] array,int i,int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}
🚩直接选择排序的特性总结
-
直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
-
时间复杂度:O(N^2)
-
空间复杂度:O(1)
-
稳定性:不稳定
🎄堆排序
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法:
-
大顶堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列;
-
小顶堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中用于降序排列;
🚩算法步骤
-
创建一个堆 H[0……n-1];
-
把堆首(最大值)和堆尾互换;
-
把堆的尺寸缩小 1,并调用 shift_down(0),目的是把新的数组顶端数据调整到相应位置;
-
重复步骤 2,直到堆的尺寸为 1。
如下图所示:

🚩代码实现:
private void swap(int[] array,int i,int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}public void heapSort(int[] array) {createBigHeap(array);int end = array.length-1;while (end > 0) {swap(array,0,end);shiftDown(array,0,end);end--;}}private void createBigHeap(int[] array) {for (int parent = (array.length-1-1)/2; parent >= 0 ; parent--) {shiftDown(array,parent,array.length);}}private void shiftDown(int[] array,int parent,int len) {int child = 2*parent+1;while (child < len) {if(child+1 < len && array[child] < array[child+1]) {child++;}if(array[child] > array[parent]) {swap(array,child,parent);parent = child;child = 2*parent+1;}else {break;}}}
🚩堆排序的特性总结
-
堆排序使用堆来选数,效率就高了很多。
-
时间复杂度:O(N*logN)
-
空间复杂度:O(1)
-
稳定性:不稳定
⭕总结
关于《【数据结构】 七大排序详解(壹)——直接插入排序、希尔排序、选择排序、堆排序》就讲解到这儿,感谢大家的支持,欢迎各位留言交流以及批评指正,如果文章对您有帮助或者觉得作者写的还不错可以点一下关注,点赞,收藏支持一下!