神经网络、前向传播、反向传播

前向传播是指将输入数据从输入层开始经过一系列的权重矩阵和激活函数的计算后，最终得到输出结果的过程。在前向传播中，神经网络会将每一层的输出作为下一层的输入，直到输出层得到最终的结果。

反向传播是指在神经网络训练过程中，通过计算损失函数的梯度，将梯度从输出层开始逆向传播到输入层，以更新每一层的权重参数。在反向传播中，通过计算梯度，可以得到每个神经元的误差，进而调整其权重和偏置，以最小化损失函数。

前向传播

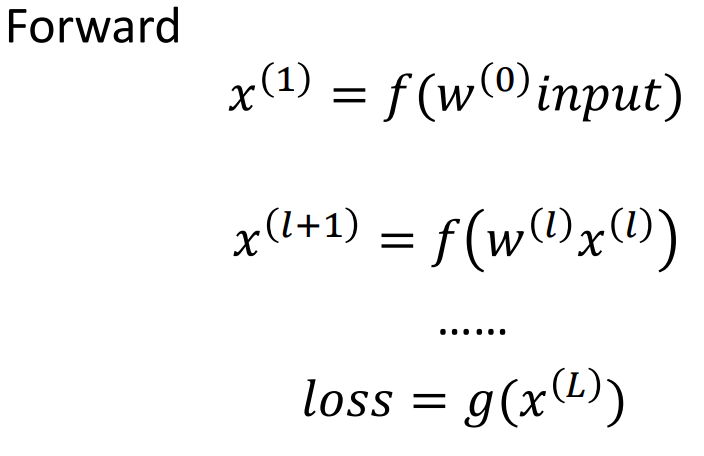
反向传播

1. 𝜕𝑙𝑜𝑠𝑠/𝜕𝑥𝐿 = 𝑔’(𝑥𝐿)
   这个公式表示输出层对输入层的偏导数，它等于激活函数关于输入的导数，即𝑔’。

2. 𝜕𝑙𝑜𝑠𝑠/𝜕𝑥𝐿−1 = 𝑊𝐿−1 · (𝜕𝑙𝑜𝑠𝑠/𝜕𝑥𝐿 ⊙ 𝑓’(𝑊𝐿−1𝑥𝐿−1))
   这个公式表示倒数第L-1层对第L层的偏导数，它等于第L层权重矩阵𝑊𝐿−1乘以(𝜕𝑙𝑜𝑠𝑠/𝜕𝑥𝐿 ⊙ 𝑓’(𝑊𝐿−1𝑥𝐿−1))，其中𝑓’表示激活函数的导数。

3. 𝜕𝑙𝑜𝑠𝑠/𝜕𝑤𝐿−1 = (𝜕𝑙𝑜𝑠𝑠/𝜕𝑥𝐿 ⊙ 𝑓’(𝑊𝐿−1𝑥𝐿−1)) · 𝑥𝐿−1
   这个公式表示对第L-1层的权重𝑤𝐿−1求偏导数，它等于(𝜕𝑙𝑜𝑠𝑠/𝜕𝑥𝐿 ⊙ 𝑓’(𝑊𝐿−1𝑥𝐿−1))乘以第L-1层的输入𝑥𝐿−1。

这些公式描述了反向传播算法中的梯度计算过程，它们用于更新神经网络中的权重以最小化损失函数。

梯度下降

假设神经网络中只有两个参数 $w_1$ 和 $w_2$。在梯度下降算法中，我们通过计算损失函数 $C$ 关于参数的偏导数来确定梯度方向，并乘以学习率 $\eta$ 来确定参数更新的步幅。这样反复迭代更新参数，直到达到收敛或满足停止条件。

具体步骤如下：

1. 随机选择一个起始点 ${\theta }_0$。
2. 计算在 ${\theta }_0$ 处的负梯度 $-\nabla C({\theta }_0)$。
3. 将负梯度与学习率 $\eta$ 相乘。
4. 更新参数：
   $${\theta }_0={\theta }_0-\eta \cdot \nabla C({\theta }_0)$$

其中，$\nabla C({\theta }_0)$ 是损失函数关于参数的偏导数组成的梯度。在二维空间中，可以表示为 $\nabla C({\theta }_0)=\left(\frac{\partial C({\theta }_0)}{\partial w_1},\frac{\partial C({\theta }_0)}{\partial w_2}\right)$。

通过不断迭代更新参数，我们可以优化网络的性能，使损失函数最小化。

局部最小值

梯度下降算法并不保证能够达到全局最小值。不同的初始点 ${\theta }_0$ 可能会收敛到不同的局部最小值，因此会得到不同的结果。

这是因为神经网络的损失函数通常是非凸的，存在多个局部最小值。在非凸损失函数的情况下，梯度下降可能会陷入局部最小值而无法达到全局最小值。这就是为什么在训练神经网络时，初始点的选择非常重要。

然而，尽管梯度下降可能无法找到全局最小值，但在实际应用中，局部最小值往往已经足够好。此外，使用正则化和其他技巧可以帮助提高算法的鲁棒性，减少陷入不良局部最小值的风险。

因此，虽然非凸损失函数可能带来挑战，但梯度下降仍然是一种有效的优化方法，广泛应用于训练神经网络和其他机器学习模型中。

多层前馈网络表示能力

只需要一个包含足够多神经元的隐层, 多层前馈神经网络就能以任意精度逼近任意复杂度的连续函数

多层前馈网络局限

• 神经网络由于强大的表示能力, 经常遭遇过拟合. 表现为：训练误差持续降低, 但测试误差却可能上升
• 如何设置隐层神经元的个数仍然是个未决问题. 实际应用中通常使用“试错法”调整

缓解过拟合的策略

• 早停：在训练过程中, 若训练误差降低, 但验证误差升高, 则停止训练
• 正则化：在误差目标函数中增加一项描述网络复杂程度的部分, 例如连接权值与阈值的平方和