目录:
- 图的基本概念
- 图和树的区别是什么?
- 无向图和有向图的概念:
- 权值
- 邻接矩阵是什么?
- 邻接矩阵的特点
- 有向图和无向图的邻接矩阵有什么区别?
- 邻接表是什么?
- 邻接表的特点
- 代码实现
- 总结
图的基本概念
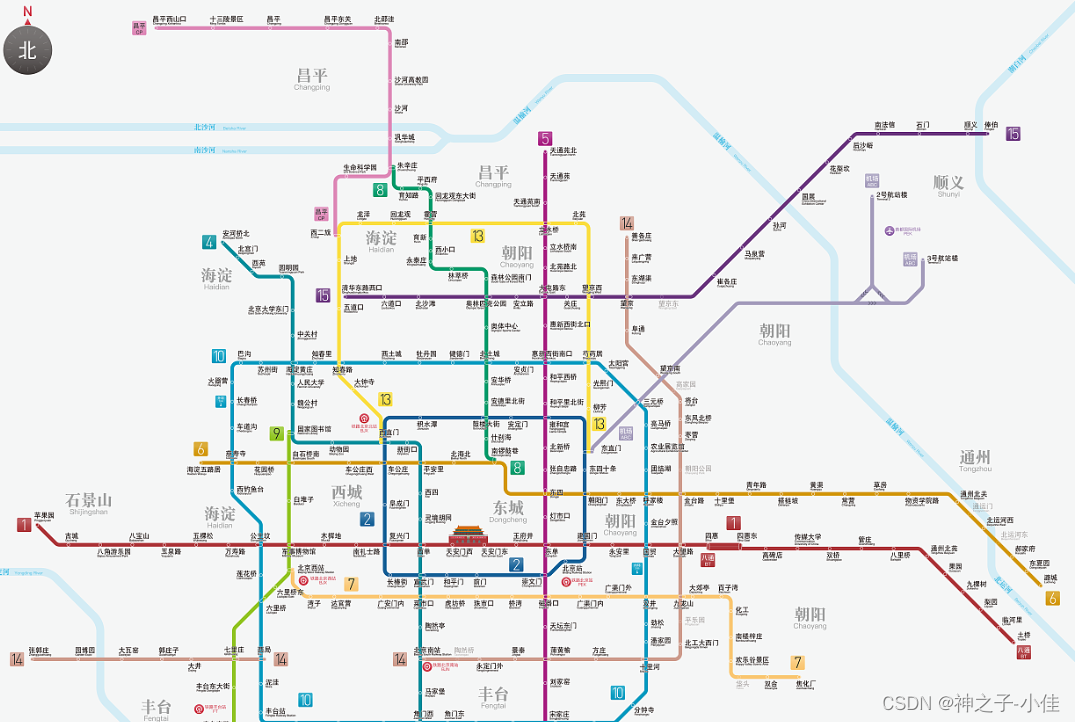
图是由顶点集合及顶点间的关系组成的一种数据结构:G=(V,E),G表示个图,V是图G中顶点的集合,E是图G中边的集合。就好比我们每天生活中乘坐的地铁,各个轨道相连接组成的地铁路线图就是一个抽象的图!
图和树的区别是什么?
1.树是一种特殊的图,图不一定是树
2.树关注的是节点中存的值,图关注的是顶点及边的权值
3.树可以是空树,但图不可以是空图,至少有一个顶点
无向图和有向图的概念:
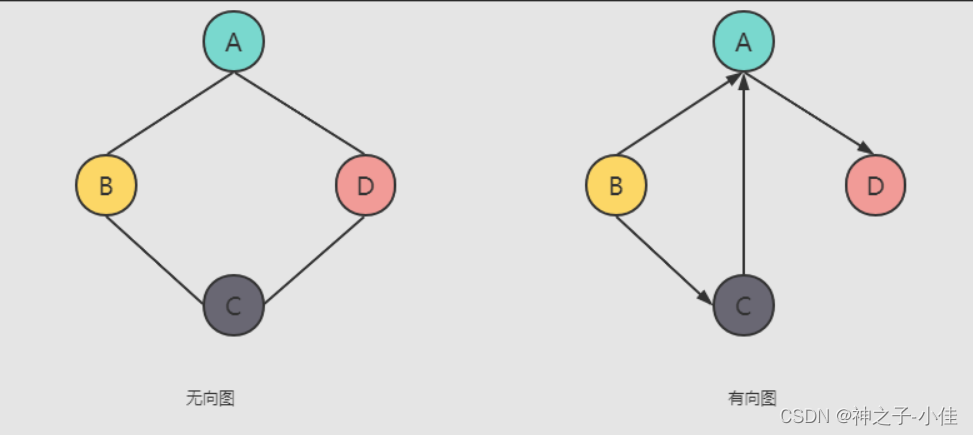
在图中,若用箭头标明了边是有方向性的,则称这样的图为有向图,否则称为无向图。
权值
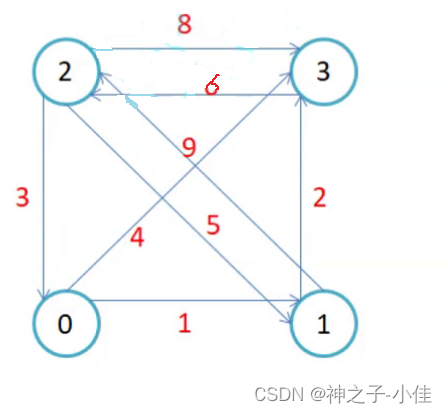
权值就是定义的路径上面的值,它的英文是weight,所以有的书上也叫权重。可以这样理解为节点间的距离,通常指字符对应的二进制编码出现的概率。边的权值就是边的权重,其意义表示链接两个结点的边的大小或者长度等。这里我们有红色数字1-8表示权值。
邻接矩阵是什么?
邻接矩阵是表示顶点之间相邻关系的矩阵,设G=(V,E)是一个图,这个图G表示V和E集合,其中,V是顶点,E是边。因此,用一个一维数组存放图中所有顶点数据;用一个二维数组存放顶点间关系(边或弧)的数据,这个二维数组称为邻接矩阵。邻接矩阵又分为有向图邻接矩阵和无向图邻接矩阵。
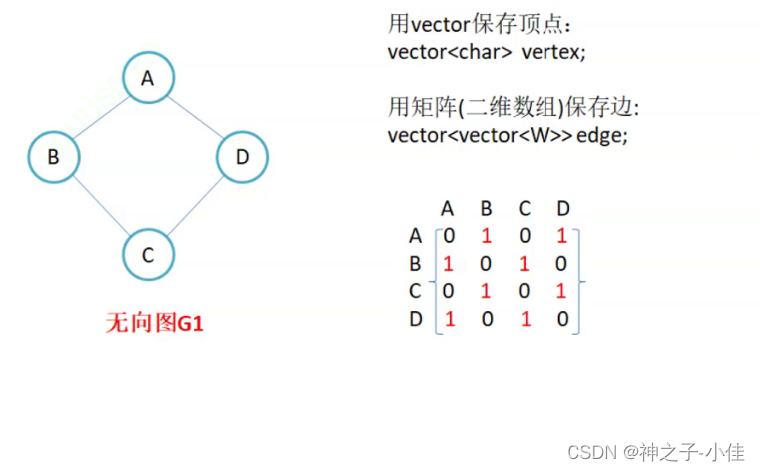
如图所示,顶点0和顶点1之间有边关联,那么矩阵中的元素A[0][1]与A[1][0]的值就是1;顶点A和顶点C之间没有边关联,那么矩阵中的元素A[0][2]与A[2][0]的值就是0。像这样表达图中顶点关联关系的矩阵,就叫做邻接矩阵。需要注意的是,矩阵从左上到右下的一条对角线,对角线上面的元素都是0,这样很容易想明白:任何一个顶点与它自身是没有连接的。同时,无向图对应的矩阵是一个对称矩阵,A和B有关联,那么B和A也必定有关联,因此A[0][1]和A[1][0]的值一定相等。
邻接矩阵的特点
1.邻接矩阵存储方式非常适合稠密图
2.领接矩阵O(1)判断另个顶点的链接关系
3.相对而言不适合查一个顶点连接所有边
有向图和无向图的邻接矩阵有什么区别?
一、对称区别:
1、无向图的邻接矩阵是对称的。
2、有向图的邻接矩阵不一定对称。
二、元素区别:
1、对于无向图,顶点V1的度是邻接矩阵中第i行(或第i列)的非零元素的个数。
2、对于有向图,顶点V1的度是邻接矩阵中第i行和第i列的非零元素的个数之和。
邻接表是什么?
使用数组表示顶点的集合,使用链表表示边的关系,比如我们可以使用vector保存所有的顶点,使用链表保存与每个顶点连通的顶点。
邻接表的特点
1.适合存储稀疏图
2.适合查找一个顶点链接出去的边
3.不适合确顶两个顶点是否相连及权值
代码实现
#pragma once
#include<vector>
#include<map>
//weight
namespace matrix
{//false表示无向图,true表示有向图//MAX_W是非类型的模板参数template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>class Graph{public:Graph(){}//手动添加边Graph(const V* a, size_t n){//如果 n 比当前 vector 容器的容量小,则该方法什么也不会做;反之如果 n 比当前 vector 容器的容量大,则 vector 容器就会扩容。_vertexs.reserve(n);for (size_t i = 0; i < n; ++i){_vertexs.push_back(a[i]);//存顶点_indexMap[a[i]] = i;//顶点找下标}_matrix.resize(n);for (size_t i = 0; i < _matrix.size(); ++i){_matrix[i].resize(n, MAX_W);}}size_t GetVerIndex(const V& v)//顶点的下标{auto it = _indexMap.find(v);if (it != _indexMap.end()){return it->second;}else{throw invalid_argument("顶点不存在");return -1;}}void AddEdge(const V& src, const V& dst, const W& w){size_t srci = GetVerIndex(src);size_t dsti = GetVerIndex(dst);_matrix[srci][dsti] = w;//false表示无向图if (Direction == false){_matrix[dsti][srci] = w;//w表示这个权值}}void Print(){for (size_t i = 0; i < _vertexs.size(); ++i){cout << "[" << i << "]" << "->" << _vertexs[i] << endl;}cout << endl;//矩阵//打印横下标cout << " ";for (size_t i = 0; i <_vertexs.size(); ++i){cout << i <<" ";}cout << endl;for (size_t i = 0; i < _matrix.size(); ++i){cout << i << " ";//竖下标for (size_t j = 0; j < _matrix.size(); ++j){//cout << _matrix[i][j] << " ";if (_matrix[i][j] == MAX_W){cout << "* ";}else{cout << _matrix[i][j] << " ";}}cout << endl;}cout << endl;}private:vector<V> _vertexs;//顶点集合map<V, int> _indexMap;//顶点映射下标关系vector<vector<W>> _matrix;//邻接矩阵};void TestGraph1(){Graph<char, int, INT_MAX, true> g("0123", 4);g.AddEdge('0', '1', 1);g.AddEdge('0', '3', 4);g.AddEdge('1', '3', 2);g.AddEdge('1', '2', 9);g.AddEdge('2', '3', 8);g.AddEdge('2', '1', 5);g.AddEdge('2', '0', 3);g.AddEdge('3', '2', 6);g.Print();}
}
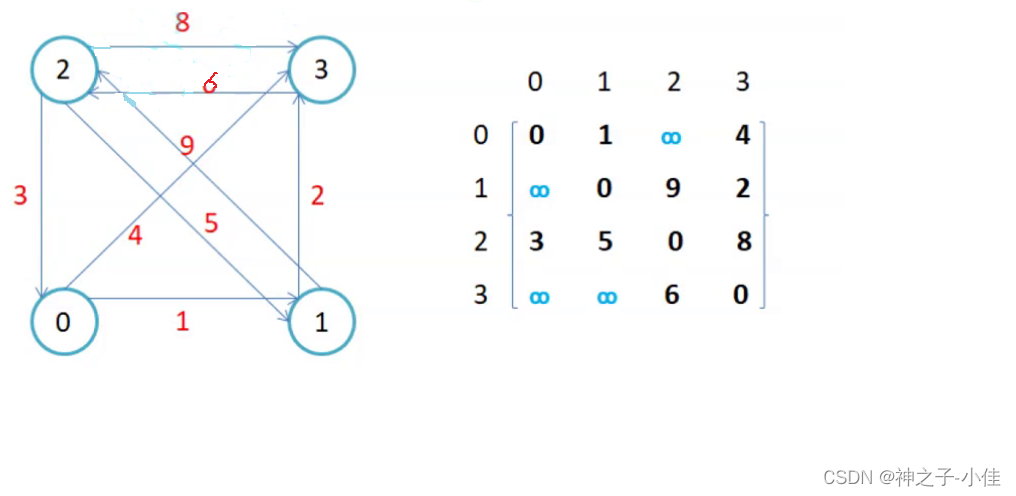
图中这样打印可下标可以清楚的看到顶点0和3是相连的,它们的权值是4,顶点1和3是相连的,它们的权值是2,顶点0和1相连它们的权值是1等。
总结
邻接矩阵和领接表其实属于相辅相成的,各有优缺点的互补结构。