一、简介

        上一篇文章，介绍了如何下载安装SDK，并且编译和下载。但都是基于SDK原生提供的demo。那本节我们就来介绍一下，如果创建一个自己的项目。

二、新建目录结构

         先看SDK提供的目录结构，如下图：

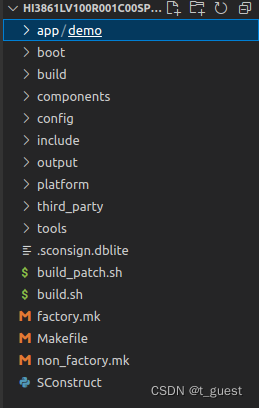
         因为是基于应用的开发，所以我们只关注app这个文件夹。可以看到app文件夹下只有一个demo文件夹，这个就是SDK提供的一个示例工程。那我们就在app下创建一个自己工程的文件夹“my_project”（这个名自己把控，这里是做个示例，方便文章讲解）。

cd SDK根目录
mkdir my_project
cd my_project
mkdir src

        创建完成后，就得到了如下的目录结构：

--my_project|
        |-src

        此外，我们还需要把灵魂文件SConscript文件拷贝过来。当然，头铁的朋友也可以自己写。

cd my_project
cp ../demo/SConscript .
cp ../demo/src/SConscript src/

        接下来，把demo目录下的app.json文件，拷贝到my_project目录下

cp ../demo/app.json .

        至此，项目<