给你一个无向图,无向图由整数 n ,表示图中节点的数目,和 edges 组成,其中 edges[i] = [ui, vi] 表示 ui 和 vi 之间有一条无向边。同时给你一个代表查询的整数数组 queries 。
第 j 个查询的答案是满足如下条件的点对 (a, b) 的数目:
a < bcnt是与a或者b相连的边的数目,且cnt严格大于queries[j]。
请你返回一个数组 answers ,其中 answers.length == queries.length 且 answers[j] 是第 j 个查询的答案。
请注意,图中可能会有 重复边 。
示例 1:
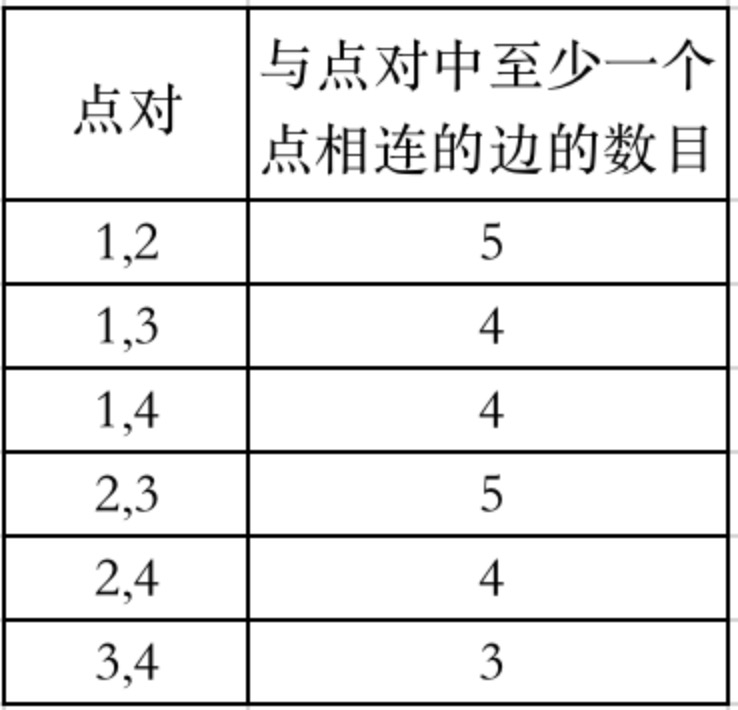
输入:n = 4, edges = [[1,2],[2,4],[1,3],[2,3],[2,1]], queries = [2,3] 输出:[6,5] 解释:每个点对中,与至少一个点相连的边的数目如上图所示。 answers[0] = 6。所有的点对(a, b)中边数和都大于2,故有6个; answers[1] = 5。所有的点对(a, b)中除了(3,4)边数等于3,其它点对边数和都大于3,故有5个。
示例 2:
输入:n = 5, edges = [[1,5],[1,5],[3,4],[2,5],[1,3],[5,1],[2,3],[2,5]], queries = [1,2,3,4,5] 输出:[10,10,9,8,6]
提示:
2 <= n <= 2 * 1041 <= edges.length <= 1051 <= ui, vi <= nui != vi1 <= queries.length <= 200 <= queries[j] < edges.length
题解:
有n个结点,m条边构成的无向图,问C(n, 2)的所有组合里有多少组合满足题设条件:对于组合(a, b),与a和b相连的边的数量大于queryNum(同一条边不重复计算)。
code:
class Solution {public int[] countPairs(int n, int[][] edges, int[] queries) {int[] degree = new int[n];Map<Integer, Integer> cnt = new HashMap<Integer, Integer>();for (int[] edge : edges) {int x = edge[0] - 1, y = edge[1] - 1;if (x > y) {int temp = x;x = y;y = temp;}degree[x]++;degree[y]++;cnt.put(x * n + y, cnt.getOrDefault(x * n + y, 0) + 1);}int[] arr = Arrays.copyOf(degree, n);int[] ans = new int[queries.length];Arrays.sort(arr);for (int k = 0; k < queries.length; k++) {int bound = queries[k], total = 0;for (int i = 0; i < n; i++) {int j = binarySearch(arr, i + 1, n - 1, bound - arr[i]);total += n - j;}for (Map.Entry<Integer, Integer> entry : cnt.entrySet()) {int val = entry.getKey(), freq = entry.getValue();int x = val / n, y = val % n;if (degree[x] + degree[y] > bound && degree[x] + degree[y] - freq <= bound) {total--;}}ans[k] = total;}return ans;}public int binarySearch(int[] arr, int left, int right, int target) {int ans = right + 1;while (left <= right) {int mid = (left + right) >> 1;if (arr[mid] <= target) {left = mid + 1;} else {right = mid - 1;ans = mid;}}return ans;}
}