递归和迭代介绍及常见示例（C++、Python实现）

递归的核心思想确实可以被概括为“分而治之”。递归通常在问题具有明显的自相似性，并且可以被有效地分解为较小的子问题时最为有效。如果一个问题不能被有效地分解，或者子问题之间有大量的重叠，那么使用递归可能不是最好的解决方案。

递归函数通常需要一个“终止条件”来指示何时停止递归。当函数调用本身时，每次参数都应该是可处理的更小数据集，以便可以逐步接近“终止条件”。

任何递归问题理论上都可以用迭代来实现，反之亦然。这是因为递归和迭代都是用来解决需要重复操作的问题的编程技术，只是它们的实现方式和效率可能会有所不同。

迭代是一种编程技术，其中一组指令被重复执行，直到满足某个条件。迭代通常通过循环结构（如 for 循环或 while 循环）实现。

以下是一些使用递归函数的例子。

1、计算了1到n的整数之和。

★递归算法用C++实现：

#include <iostream>
using namespace std; int recursiveSum(int n) {if (n == 0) { // 终止条件return 0;} else {return n + recursiveSum(n - 1); // 递归调用}
}int main() {int n;cout << "请输入一个正整数: ";cin >> n;int sum = recursiveSum(n); // 调用递归函数计算和cout << "从1到" << n << "的所有整数的和为: " << sum << endl;return 0;
}

★递归算法用Python实现代码：

def recursiveSum(n):if n == 0:return 0else:return n + recursiveSum(n - 1); # 递归调用n = int(input("请输入一个正整数: "))
sum = recursiveSum(n)  # 调用递归函数计算和print(f"从1到{n}的所有整数的和为: {sum}")  

★迭代算法用c++实现：

#include <iostream>
using namespace std; int iterativeSum(int n) {int sum = 0;for(int i = 1; i <= n; i++) {sum += i;}return sum;
}int main() {int n;cout << "请输入一个正整数: ";cin >> n;int sum = iterativeSum(n); // 调用递归函数计算和cout << "从1到" << n << "的所有整数的和为: " << sum << endl;return 0;
}

★迭代算法用Python实现：

def iterativeSum(n):result = 0while n > 0:result += nn -= 1return resultn = int(input("请输入一个正整数: "))
sum = iterativeSum (n)  # 调用递归函数计算和print(f"从1到{n}的所有整数的和为: {sum}")  

2.计算阶乘

阶乘（Factorial）：

阶乘是指将一个正整数 n 及小于等于 n 的所有正整数相乘的结果。符号通常用符号 "!" 表示。例如，5 的阶乘表示为 5!，计算公式为：5! = 5 × 4 × 3 × 2 × 1 = 120。可以使用递归或迭代的方式来计算阶乘。

★递归算法用C++实现（关键代码）：

int factorial(int n) {if (n == 0) {return 1;} else {return n * factorial(n - 1);}
}

在这个例子中，factorial(n)函数通过递归调用自身来计算n的阶乘。基本情况是n == 0，此时函数返回1。在递归情况下，函数返回n * factorial(n - 1)，这是n的阶乘的定义。

★递归用Python实现（关键代码）：

def factorial(n):if n == 0:return 1else:return n * factorial(n - 1)

★迭代算法用C++实现（关键代码）：

int factorial(int n) {int result = 1;for (int i = 1; i <= n; i++) {result *= i;}return result;
}

★迭代算法用Python实现（关键代码）：

def factorial_iterative(n):result = 1for i in range(1, n+1):result *= ireturn result

3.计算斐波那契数列

斐波那契数列（Fibonacci Sequence）：

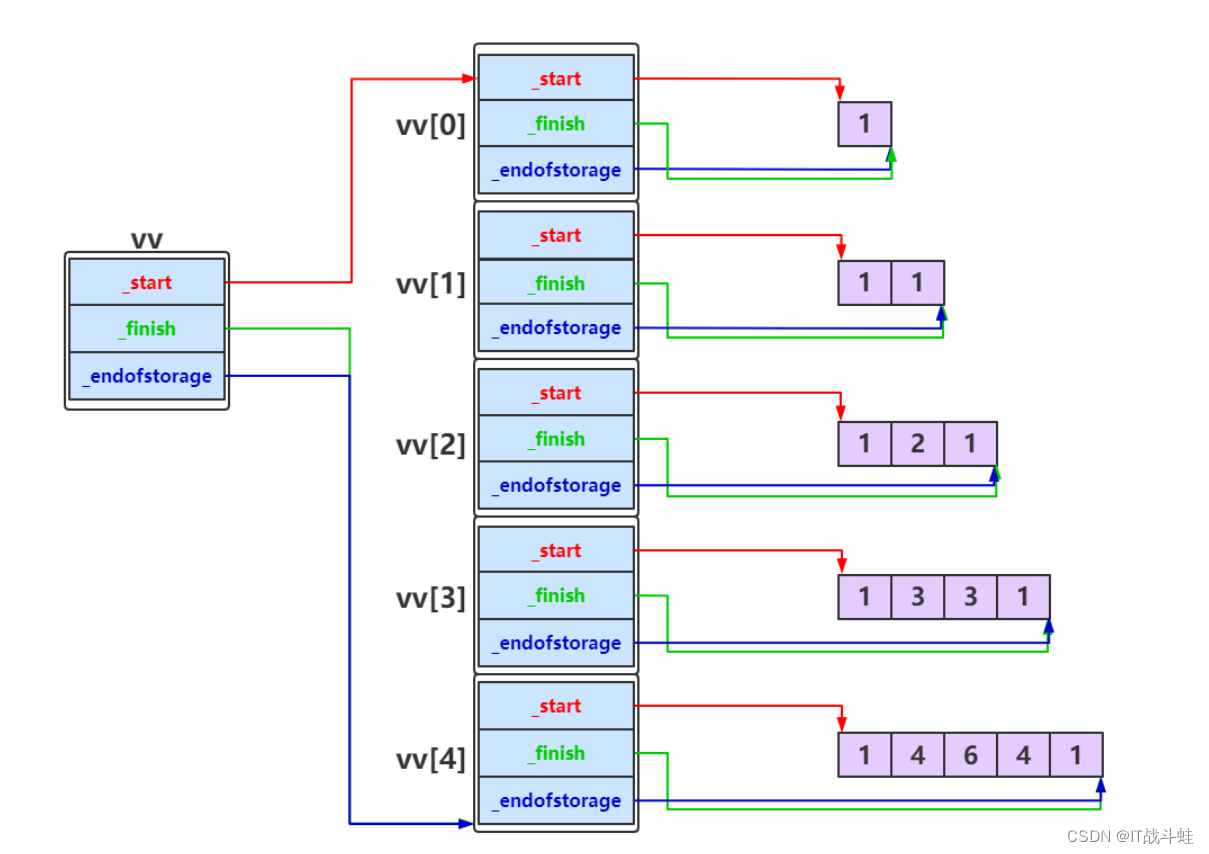
斐波那契数列是指从 0 和 1 开始，后面的每一项都是前两项之和。也就是说，第 n 个斐波那契数等于第 n-1 个斐波那契数与第 n-2 个斐波那契数的和。斐波那契数列的前几项依次为：0, 1, 1, 2, 3, 5, 8, 13, 21, ...。可以使用递归或迭代的方式来生成斐波那契数列。

★递归算法用C++实现（关键代码）：

int fibonacci(int n) {if (n <= 1) {return n;} else {return fibonacci(n - 1) + fibonacci(n - 2);}
}

在这个例子中，fibonacci(n)函数通过递归调用自身来计算斐波那契数列的第n项。基本情况是n <= 1，此时函数返回n。在递归情况下，函数返回fibonacci(n - 1) + fibonacci(n - 2)，这是斐波那契数列的定义。

★递归算法用Python实现（关键代码）：

def fibonacci(n):if n <= 1:return nelse:return fibonacci(n - 1) + fibonacci(n - 2)

★迭代算法用C++实现（关键代码）：

int fibonacci(int n) {if (n <= 0) {return n;} else {int a = 0, b = 1, c;for (int i = 2; i <= n; i++) {c = a + b;a = b;b = c;}return b;}
}

★迭代算法用Python实现（关键代码）：

def fibonacci(n):if n <= 0:return nelse:a, b = 0, 1for _ in range(2, n + 1):a, b = b, a + breturn b