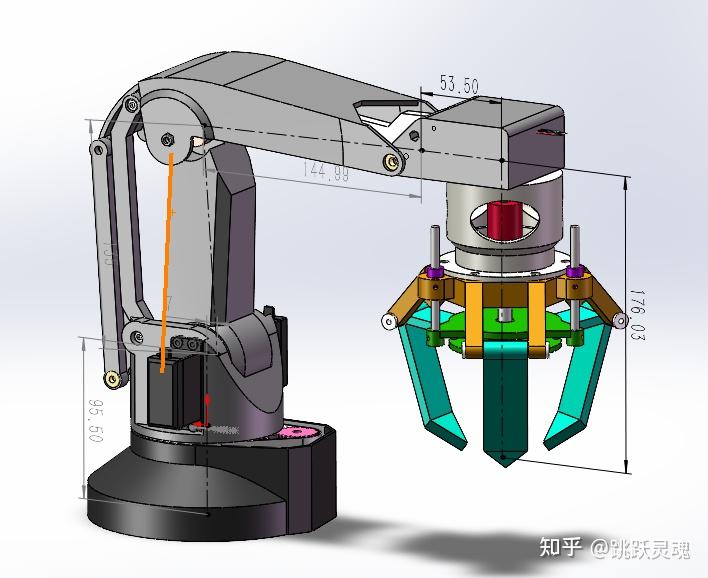
1正运动学分析
采用标准的D-h法进行机械腿模型分析:
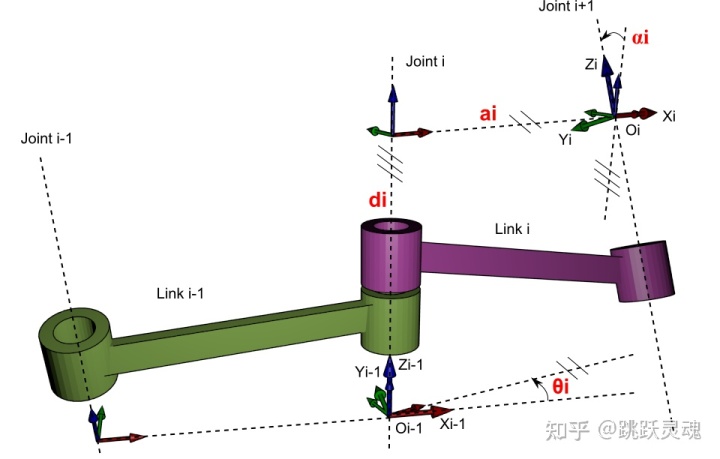

D-h表如下

(2)通过(1)求解出机器人各位姿变换矩阵后,求解机器人手臂变换矩阵
**
**
。通过matlab 计算,写出机器人末端位置。
正运动学分析
根据D-H表规定得到如下变换矩阵为:

根据DH参数求解变换矩阵的函数trans:
%输入JD,即6个关节变量的值,求解正运动方程
function [ T ] = trans( theta, d, a, alpha )
T =[
cos(theta), -sin(theta)*cos(alpha), sin(theta)*sin(alpha), a*cos(theta);
sin(theta), cos(theta)*cos(alpha), -cos(theta)*sin(alpha), a*sin(theta);
0, sin(alpha), cos(alpha), d;
0, 0, 0, 1 ];
end
正向运动学:
function [ T06 ] = fkine(JD)
%JD为输入的1*6的数组,代表6个关节变量
% trans( theta, d, a, alpha )
if nargin<2; end
T01 =trans( JD(1), 0.0955, 0.007, pi/2 );
T12 =trans( JD(2)+pi/2, 0, 0.135, 0);
T23 =trans( JD(3)-pi/2, 0, 0.145, 0);
T34 =trans( JD(4), 0, 0.0535, pi/2 );
T45 =trans( JD(5), 0.176, 0, -pi/2 );
T06 =T01*T12*T23*T34*T45;
end
3机器人模型建立
所设计的机器人由多个连杆机构组成,其关节类型包括旋转关节和移动关节两种。利用Matlab中机器人仿真工具箱Robotics Tool中Link和SerialLink两个函数可建立机器人模型[]。其中,函数表达式如下:
式中,theta为关节变量;_d_为偏置距离;alpha为扭转角;_a_为连杆长度;sigma表示关节类型(0为旋转关节,1为移动关节);前四个参数分别对应表1中的
,
具体程序编制如下:
Clear %情况matlab软件的数据缓存,避免影响本次运行
Clc %清空运行窗口的数据
L(1) = Link( ‘d’, 0.0955, ‘a’ , 0.007 , ‘alpha’, pi/2 ,‘offset’,0);
L(2) = Link( ‘d’, 0 , ‘a’ ,0.135 , ‘alpha’, 0, ‘offset’,pi/2);
L(3) = Link( ‘d’, 0 , ‘a’ , 0.145 , ‘alpha’,0 ,‘offset’,-pi/2);
L(4) = Link( ‘d’, 0 , ‘a’ ,0.0535 , ‘alpha’, pi/2 ,‘offset’,0);
L(5) = Link( ‘d’, 0.176 , ‘a’ , 0 , ‘alpha’, -pi/2 ,‘offset’,0);
robot = SerialLink(L, ‘name’ , ‘机械臂’); %建立四自由度模型
% RRP.plotopt = {‘workspace’,[-10,10,-10,10,-10,10],‘tilesize’,10}; %设置模型空间大小和地砖大小
robot.teach; %画出模型并进行调控
robot.display(); %显示建立的机器人的DH参数robot.plot([0 0 0 0 0])%输入一定参数后机器人图形
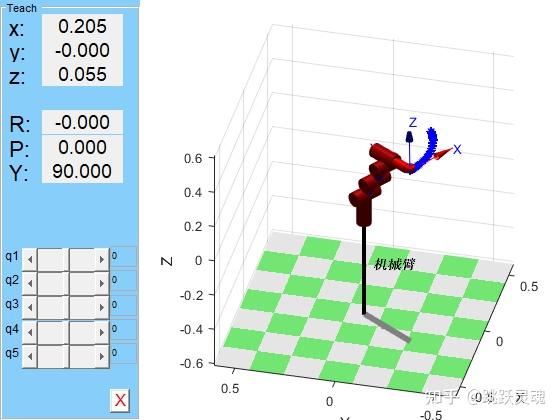
运行上述程序,即可得到码垛机器人模型如图 3-3
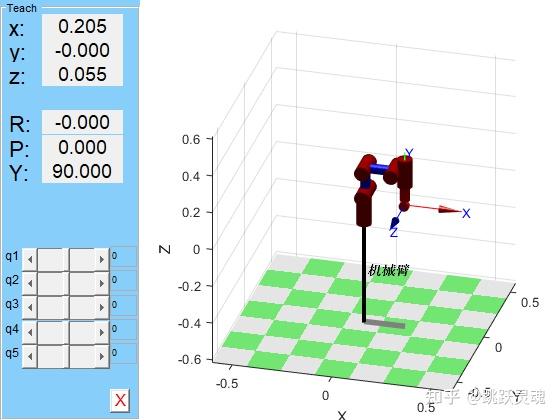
图 3-3机器臂模型
4机器臂正运动验证
init_ang=[0,-pi/4,0,-pi/5,0,0];%p1起点
disp(‘工具箱求解得到旋转矩阵如下:’)
robot.fkine(init_ang)
%%
%自定义矩阵
disp(‘通过变换矩阵求解旋转矩阵如下:’)
fkine(init_ang)
robot.plot([0,-pi/4,0,-pi/5,0,0])
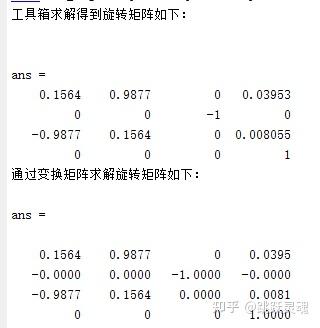
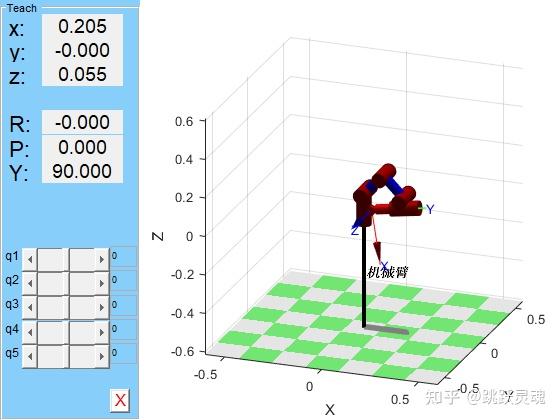
如图所示:任意选取某点工具箱仿真姿态结果与变换矩阵计算结果一致。验证了正运动学方程的正确性。
轨迹规划程序
L(1) = Link( ‘d’, 0.0955, ‘a’ , 0.007 , ‘alpha’, pi/2 ,‘offset’,0);
L(2) = Link( ‘d’, 0 , ‘a’ ,0.135 , ‘alpha’, 0, ‘offset’,pi/2);
L(3) = Link( ‘d’, 0 , ‘a’ , 0.145 , ‘alpha’,0 ,‘offset’,-pi/2);
L(4) = Link( ‘d’, 0 , ‘a’ ,0.0535 , ‘alpha’, pi/2 ,‘offset’,0);
L(5) = Link( ‘d’, 0.176 , ‘a’ , 0 , ‘alpha’, -pi/2 ,‘offset’,0);
% L(6) = Link( ‘d’, 0.134 , ‘a’ ,0 , ‘alpha’, 0 ,‘offset’,0);
robot = SerialLink(L, ‘name’ , ‘机械臂’); %建立四自由度模型
% RRP.plotopt = {‘workspace’,[-10,10,-10,10,-10,10],‘tilesize’,10}; %设置模型空间大小和地砖大小
robot.teach; %画出模型并进行调控
robot.display(); %显示建立的机器人的DH参数
% robot.plot([0 0 0 0 0])%输入一定参数后机器人图形
%利用五次多项式轨迹规划
T1=transl(0.3,-0.3,0.5)%起点
q1=robot.ikunc(T1);
T2=transl(-0.3,-0.2,0.4)%终点
q2=robot.ikunc(T2);
[qt1,qt2,qt3]=jtraj(q1,q2,50);
hold on
robot.plot(qt1, ‘trail’,‘-b’)
qt=robot.fkine(qt1)
T=transl(qt);
plot3(T(:,1),T(:,2),T(:,3) ,‘*b’);%输出末端轨迹
需要三维模型+程序+报告可私聊我