一、介绍

        学习排名 （LTR） 是一类监督式机器学习算法，旨在根据项目与查询的相关性对项目列表进行排序。在分类和回归等问题中的经典机器学习中，目标是根据特征向量预测单个值。LTR 算法对一组特征向量进行操作，并预测项目的最佳顺序。

        LTR 有许多不同的应用。以下是其中的一些：

• 搜索引擎。用户在浏览器搜索栏中键入查询。搜索引擎应该对网页进行排名，使最相关的结果出现在顶部位置。
• 推荐系统。电影推荐系统根据输入查询选择应向用户推荐哪部电影。

        让我们正式定义排名问题：

给定一个存储有关查询和文档信息的 n 维特征向量，排名的目标是找到这样一个函数 f，该函数产生一个实数，指示查询与文档的相关性。此外，如果对象 i 的排名高于对象 j （i ▷ j），则 f（i） 应大于 f（j）。

注意。i ▷ j 表示文档 i 的排名高于文档 J。

二、数据

2.1 特征向量

        特征向量由三种类型的特征组成：

• 仅从文档派生的特征（例如，文档长度、文档中的链接数）。
• 仅从查询派生的特征（例如，查询长度、查询频率）。
• 从文档和查询的组合派生的特征（例如，TF-IDF、BM25、BERT、文档中常用单词的数量和查询）

2.2 训练数据

        为了训练模型，我们需要将输入到模型中的训练数据。根据训练数据的收集方式，有两种可能的方法。

• 离线 LTR。数据由人工手动注释。人工对不同查询和文档的对（查询、文档）的相关性进行评分。这种方法既昂贵又耗时，但提供了高质量的注释。
• 在线LTR。数据是从用户与查询结果的交互中隐式收集的（例如，排名项目的点击次数、在网页上花费的时间）。在这种情况下，获取训练数据很简单，但用户交互不容易解释。

之后，我们有特征向量和与之对应的标签。这就是我们训练模型所需的一切。下一步是为问题选择最适合的机器学习算法。

三、排名类型

        从高层次来看，大多数 LTR 算法使用随机梯度下降来找到最佳排名。根据算法在每次迭代中选择和比较项目排名的方式，存在三种主要方法：

• 逐点排名。
• 成对排名。
• 按列表排名。

        所有这些方法都将排名任务转换为分类或回归问题。在以下部分中，我们将看到它们如何在引擎盖下运行。

3.1 逐点排名

        在逐点方法中，为每个特征向量单独预测分数。最终，对预测的分数进行排序。使用哪种类型的模型（决策树、神经网络等）进行预测并不重要。

这种类型的排序将排名问题转换为回归任务，其中回归模型试图预测与所选损失函数（例如，MSE）的正确相关性。

另一种有效的方法是将真实值排名转换为独热表示，并将此数据提供给模型。在这种情况下，可以使用回归或分类模型（具有交叉熵损失）。

逐点模型体系结构。作为输入，模型接受查询和特征向量。

尽管该方法非常简单，但它存在下面列出的一些问题。

阶级失衡

使用逐点方法时的一个常见问题是类不平衡。如果在现实生活中进行随机查询，那么很可能集合中所有文档中只有一小部分与之相关。因此，在训练数据中，查询的相对和非相关文档之间存在高度不平衡。

虽然可以克服这个问题，但还有一个更严重的问题需要考虑。

糟糕的优化指标

逐点排名的优化目标存在一个主要的基本问题：

逐点排名独立优化文档分数，不考虑不同文档之间的相对分数。因此，它不会直接优化排名质量。

考虑下面的一个示例，其中逐点算法对两组文档进行了预测。我们假设 MSE 损失在训练期间得到优化。

集合包含 5 个文档，其中 1 个文档相关，其他 4 个不相关。对于相关文档，预测相关性为 0.7，而对于其他文档，预测相关性为 0.5。

        集合包含 5 个文档，其中 1 个文档相关，其他 4 个不相关。对于相关文档，预测相关性为 0.1，而对于其他文档为 0.2。

给定两个排名结果，我们可以看到，从算法的角度来看，第二个排名更好，因为相应的MSE值较低。但是，选择第二个排名意味着首先将向用户显示所有不相关的结果。顺便说一下，在第一个示例中，首先显示了相关结果，从用户体验来看要好得多。通常，用户不会过多关注之后的建议。

        这个例子表明，在现实生活中，我们首先更关心的是显示相关结果以及项目的相对顺序。通过独立处理文件，逐点不保证这些方面。较低的损失并不等同于更好的排名。

3.2 成对排名

        成对模型在每次迭代时都使用一对文档。根据输入格式，有两种类型的成对模型。

3.2.1 配对输入模型

        模型的输入是两个特征向量。模型输出是第一个文档排名高于第二个文档的概率。在训练期间，针对不同的特征向量对计算这些概率。模型的权重通过基于地面实况等级的梯度下降进行调整。

配对输入模型体系结构。作为输入，模型接受一个查询和两个串联的特征向量。

此方法在推理过程中有两个主要缺点：

• 为了在推理过程中对给定查询的 n 个文档进行排名，模型需要处理其中的每一对文档，以获得所有成对概率。对的总数是二次的（正好等于 n * （n — 1） / 2），效率非常低。
• 即使拥有所有文档的成对概率，最终如何对它们进行排名也不明显，尤其是在像恶性循环这样的矛盾情况下，当存在三元组文档（x，y，z）时，模型以以下方式进行排名：x ▷ y，y ▷ z 和 z ▷ x。

恶性循环问题

由于这些缺点，配对输入模型在实践中很少使用，单输入模型优于它们。

3.2.2 单输入型号

        该模型接受单个特征向量作为输入。在训练期间，一对中的每个文档都独立地馈送到模型中以接收自己的分数。然后比较两个分数，并根据地面真实等级通过梯度下降调整模型。

单输入模型架构。作为输入，该模型采用查询和表示文档的单个特征向量。排名预测是在模型独立地将分数分配给两个特征向量后计算的。

在推理过程中，每个文档通过传递给模型来获得一个分数。然后对分数进行排序以获得最终排名。

对于那些熟悉Siamese网络（FaceNet，SBERT，e.t.c）的人来说，单输入模型可以被认为是Siamese网络。

3.2.3 成对损失函数

        在每次训练迭代期间，模型都会预测一对文档的分数。因此，损失函数应该是成对的，并考虑两个文档的分数。

        一般来说，成对损失将两个分数 s[i] — s[j] 之间的差乘以常数σ作为其参数 z。根据算法的不同，损失函数可以具有以下形式之一：

        

成对排序的不同损失函数

有时分数差 z 可以乘以一个常数。

RankNet是最流行的成对排名算法之一。我们将在下一节中查看其实现的详细信息。

3.2.4 排名网

        在获得文档 i 和 j 的分数后，RankNet 使用 softmax 函数对其进行规范化。通过这样做，RankNet 获得了文档 i 排名高于文档 j 的概率 P[i][j] = P（i ▷ j）。 相反，我们可以计算概率 P̃[j][i] = P（j ▷ i） = 1 — P（i ▷ j）。为简单起见，我们假设在现实中 i 的排名更高 j，因此 P̃[i][j] = 1 且 P̃[j][i] = 0。对于模型权重的更新，RankNet使用交叉熵损失，其简化方式如下：

        排名净亏损函数

        模型的权重由梯度下降调整。下次模型获得同一对文档 i 和 j 时，文档 i 可能会获得比以前更高的分数，并且文档 j 可能会被推下。

RankNet 分解

为简单起见，我们不打算深入研究数学，但在原始论文中提出了一个有趣的研究结果，作者找到了一种简化训练过程的方法。这是通过引入变量 S[i][j] 来完成的，该变量采用三个可能的值之一：

经过一些数学技巧，交叉熵损失的导数分解为：

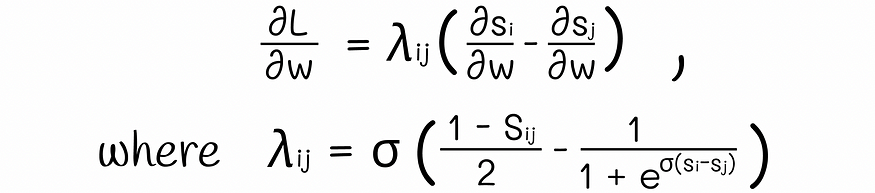
公式中的 lambda 值是一个常量，可以相对快速地为所有文档对计算。通过取正值或负值，这些 lambda 充当推动文档向上或向下的力。

我们可以总结单个文档 i 的所有成对 lambda。此总和得出应用于排名中文档 i 的总力。

汇总 lambda 以查找应用于文档的总力

使用 lambda 直接导致更快的训练时间和更好的结果解释。

尽管成对算法的性能优于逐点方法，但它们有两个缺点。

不可解释的概率

模型的输出概率只是表明模型对某个对象 i 的排名高于对象 j 的置信度。然而，这些概率不是真实的，有时可以通过模型粗略地近似，所以总是使用它们进行解释不是一个好主意，尤其是在我们之前看到的恶性循环混淆的情况下。

最小化反转不是最佳的

这个问题比前一个问题要严重得多。大多数成对算法，特别是RankNet的根本问题是它们最大限度地减少了秩倒置的数量。虽然优化反转数量似乎很自然，但实际上这并不是大多数最终用户想要的。请考虑以下示例，其中包含两个排名。在您看来，哪个排名更好？

两个相关文件位于列表的开头和末尾。

两个相关文档位于列表中间的左侧。

虽然第二个排名的反转较少，这是算法的优先级，但普通用户仍然更喜欢第一个排名，因为顶部至少有一个相关结果。这意味着用户不必滚动浏览大量文档即可找到第一个相关结果。同样，最好使用nDCG或ERR等面向用户的指标，它们更强调顶级结果而不是反转次数。

因此，我们可以看到并非所有文档对都同样重要。算法需要调整，使其更加重视在顶部而不是底部获得正确的排名。

该论文的研究人员提出了一个说明良好的示例，说明使用RankNet优化排名如何导致非最佳结果：

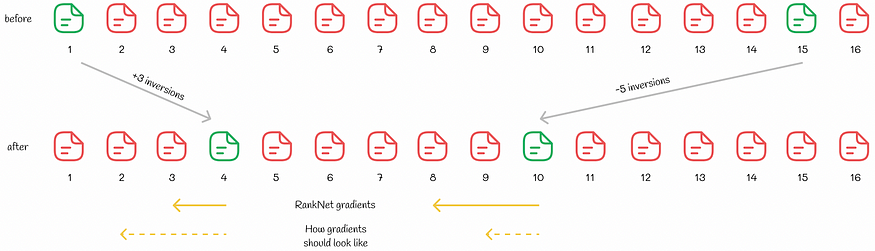
我们可以看到，第 1 位的文档被推到了第 4 位，第 15 位文档被推到了第 10 位，因此反转总数减少了 2。然而，从用户体验来看，新的排名变得更糟。核心问题在于，RankNet为位置较差的文档分配了更大的梯度。但是，为了优化面向用户的指标，这应该相反：位置较好的文档应该比位置较差的文档进一步推高。这样，像nDCG这样的面向用户的指标将会更高。

3.3 按列表排名

        列表算法明确优化排名指标。要优化具有梯度下降的某个指标，需要为该指标计算导数。不幸的是，大多数排名指标（如nDCG或精度）都是非连续且不可微分的，因此发明了其他先进技术。

        与逐点或成对排名不同，列表方法一次将整个文档列表作为输入。有时这会导致大计算，但也提供了更多的鲁棒性，因为算法在每次迭代时都会提供更多信息。

列表模型体系结构。作为输入，该模型采用所有文档的查询和特征向量。

3.3.1 LambdaRank

根据实现的不同，可以将 LambdaRank 视为成对或列表方法。

当关注 nDCG 时，似乎最好为位置交换导致更高 nDCG 的文档对分配较大的梯度。这个核心思想在于LambdaRank。

算法名称中的“lambda”暗示LambdaRank也使用RankNet中描述的lambda进行优化。

研究人员产生了惊人的结果，并证明如果将RankNet中的损失值乘以|nDCG|，那么该算法倾向于直接优化nDCG！也就是说，LambdaRank算法与RankNet非常相似，除了这次lambda乘以nDCG变化：

nDCG优化公式

这项研究的不可思议之处在于，这个技巧不仅适用于nDCG，也适用于其他信息检索指标！同样，如果 lambda 乘以精度变化，则精度将得到优化。

最近，理论上证明 LambdaRank 优化了某些信息检索指标的下限。

3.3.2 其他方法

        我们不会详细讨论其他列表方法的工作原理，但仍然提供其实现两个光荣算法背后的主要思想。

        LambdaMart 是列表方法的著名实现，该方法使用梯度提升树和源自 LambdaRank 的损失函数。在实践中，它的性能优于LambdaRank。

      SoftRank解决了nDCG的衍生存在问题。它创建了一个称为“SoftNDCG”的新指标，该指标平滑地表示和近似 nDCG，从而可以找到相应的导数并通过梯度下降更新模型的权重。事实上，这种方法同样可以应用于其他指标。

四、结论

        我们已经介绍了排名 - 机器学习中的一项重要任务，用于按相关顺序对一组对象进行排序。逐点和成对方法不经常使用，而按列表方法最可靠。显然，我们只讨论了排名算法的一小部分，但这些信息对于理解更复杂的技术（如ListNet或ListMLE）至关重要。可以在此处找到列表算法的广泛列表。

        值得注意的是，LambdaRank是目前最先进的排名算法之一，它为优化特定指标提供了很大的灵活性。

        如果您想找到有关排名指标的更多信息，我强烈建议您阅读我关于此主题的另一篇文章。

五、资源

• 从RankNet到LambdaRank再到LambdaMART：概述
• 学习使用梯度下降进行排名
• 信息检索 |学习排名 |哈里·奥斯特赫伊斯
• 学习排名 |维基百科
• 软排名：优化非平滑排名指标

 有图片均由作者提供 维亚切斯拉夫·叶菲莫夫