- (꒪ꇴ꒪ ),Hello我是祐言QAQ
- 我的博客主页:C/C++语言,Linux基础,ARM开发板,软件配置等领域博主🌍
- 快上🚘,一起学习,让我们成为一个强大的攻城狮!
- 送给自己和读者的一句鸡汤🤔:集中起来的意志可以击穿顽石!
- 作者水平很有限,如果发现错误,可在评论区指正,感谢🙏

一、什么是图
图是一种由节点(顶点)和连接这些节点的边构成的非线性数据结构。每个节点可以表示一个实体,而边则表示节点之间的关系。图的设计可以用于模拟现实世界中的各种复杂关系和连接,从社交网络到通信网络,都可以通过图来更好地理解和分析。
二、图的分类
图可以根据多个维度进行分类:
- 有向图(Directed Graph)和无向图(Undirected Graph): 有向图中的边具有方向,表示从一个节点指向另一个节点的关系;而无向图中的边没有方向,表示两个节点之间的对等关系。

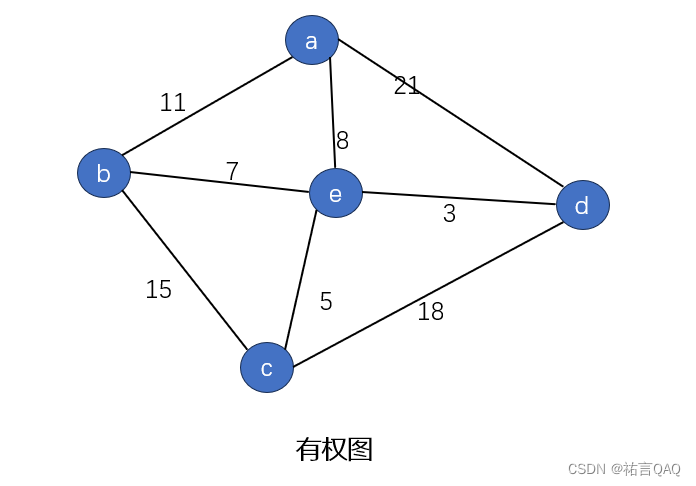
- 有权图(Weighted Graph)和无权图(Unweighted Graph): 在有权图中,每条边都有一个权重,可以表示节点之间的某种度量,如距离、成本等;而在无权图中,边没有权重,只表示连接关系。
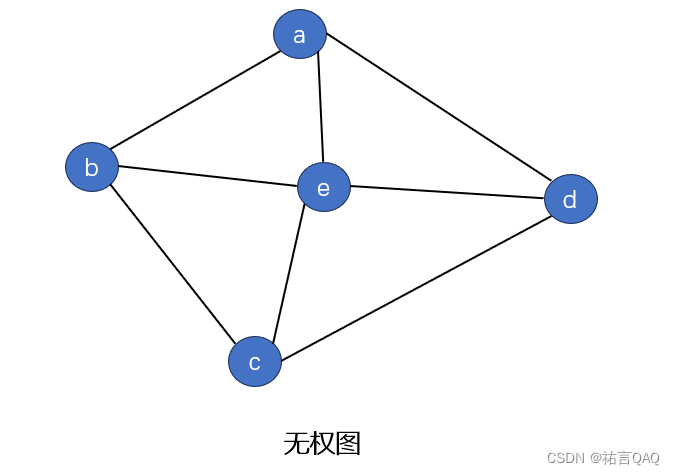
- 简单图和多重图(Multigraph): 简单图中不存在自环和重复的边;而多重图允许自环和可能具有相同的边。
三、图的边
图的边是连接节点的实体,它可以包含以下信息:
- 权重(Weight): 如果是有权图,每条边都有一个权重,代表节点之间的某种度量。
- 方向: 在有向图中,边从一个节点指向另一个节点,有方向性;在无向图中,边没有方向,表示双向关系。
- 标签(Label): 可以为边添加标签,表示连接的类型或特性。
有些图的边或弧具有与它相关的数字,这种与图的边或弧相关的数叫做权,表示从一个顶点到另一个顶点的距离或花费或时间。我们称这种带权的图为网。如下图所示,即为网。
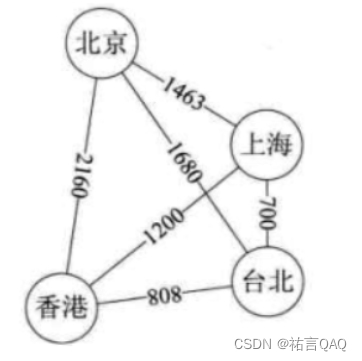
四、图的表达方式
图可以使用不同的数据结构来表示:
- 邻接矩阵(Adjacency Matrix): 使用二维数组表示图的顶点之间的连接关系。矩阵的行和列分别代表顶点,矩阵元素表示边的存在与否或权重。

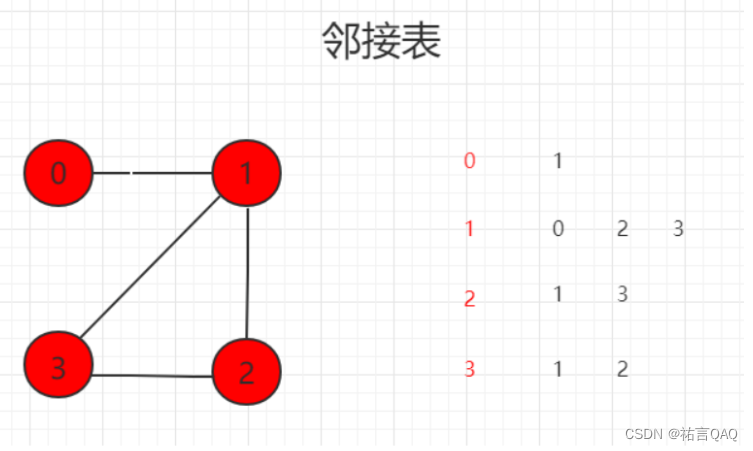
图中 1 表示相连接,0 表示不相连
- 邻接表(Adjacency List): 使用链表或数组表示图的顶点以及与其相邻的顶点。每个顶点对应一个列表,包含与之相连的顶点。
五、图的遍历
图遍历是访问图中所有节点的方法,有两种主要方法:
- 深度优先搜索(DFS): 从起始节点开始,沿着一条路径尽可能深入,直到无法继续为止,然后回溯到之前的节点,继续探索其他路径。
1.遍历思路
- 访问顶点v;
- 从v的未被访问的邻接点中选取一个顶点w,从w出发进行深度优先遍历;
- 重复上述两步,直至图中所有和v有路径相通的顶点都被访问到。
2.列举
按深度优先遍历就是:A B C D E F G H(此时这条线路已经走到尽头,可是还有一个I顶点没有遍历,所以回到G,发现G的邻接点都遍历过了,再回到F,发现F的邻接点也都遍历过了,直到D顶点,发现I这个顶点没有遍历,所以把I再遍历,继续回溯,最终回到起点A。

- 广度优先搜索(BFS): 从起始节点开始,先访问所有与其直接相邻的节点,然后逐层向外扩展,确保先访问离起始节点近的节点。
1.遍历思路
- 从图中某个顶点V0出发,并访问此顶点;
- 从V0出发,访问V0的各个未曾访问的邻接点W1,W2,…,Wk;然后,依次从W1,W2,…,Wk出发访问各自未被访问的邻接点;
- 重复步骤2,直到全部顶点都被访问为止。
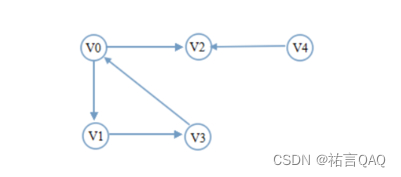
2.列举
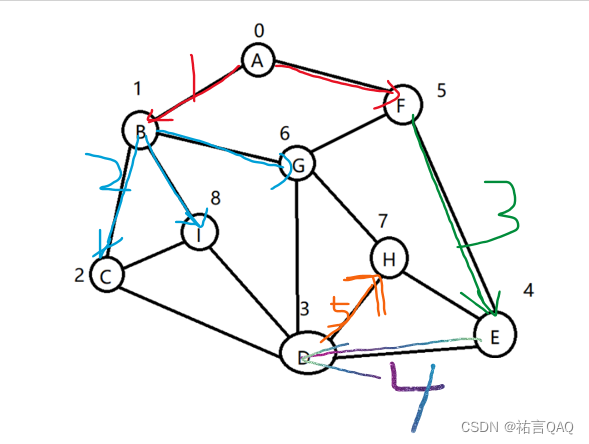
六、图的算法
图的算法是一个重要的主题,包括最短路径、连通性、最大流、最小生成树等问题。比如Dijkstra算法可以用于寻找图中的最短路径,Kruskal算法和Prim算法可以用于求解最小生成树问题。这些算法的选择和应用取决于图的特性和问题的需求。
七、适用说明
图的应用范围广泛,包括但不限于:
- 社交网络分析: 用于分析人际关系、社区发现、信息传播等。
- 路线规划: 帮助找到最短路径、最优路线,应用于导航和交通规划。
- 计算机网络: 描述计算机之间的连接、拓扑结构,用于网络设计和分析。
- 编译器: 用于构建控制流图、数据依赖图,进行代码优化和分析。
图还可以用于生物信息学(比如在蛋白质相互作用网中寻找功能模块)、物联网(比如在设备间建立最优的通信路径)等领域。
总之,图是一个强大的数据结构,能够捕捉和表示各种实体之间的关系,为解决各种复杂问题提供了有效的工具。不同类型的图和图遍历算法可以根据问题的性质和需求来选择使用。
更多C语言、Linux系统、ARM板实战和数据结构相关文章,关注专栏:
手撕C语言
玩转linux
脚踢数据结构
6818(ARM)开发板实战
📢写在最后
- 今天的分享就到这啦~
- 觉得博主写的还不错的烦劳
一键三连喔~ - 🎉感谢关注🎉