计数排序概念

计数排序是一个非基于比较的排序算法，元素从未排序状态变为已排序状态的过程，是由额外空间的辅助和元素本身的值决定的。该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范围），快于任何比较排序算法。当然这是一种牺牲空间换取时间的做法，而且当的时候其效率反而不如基于比较的排序，因为基于比较的排序的时间复杂度在理论上的下限是。

计数排序算法思路

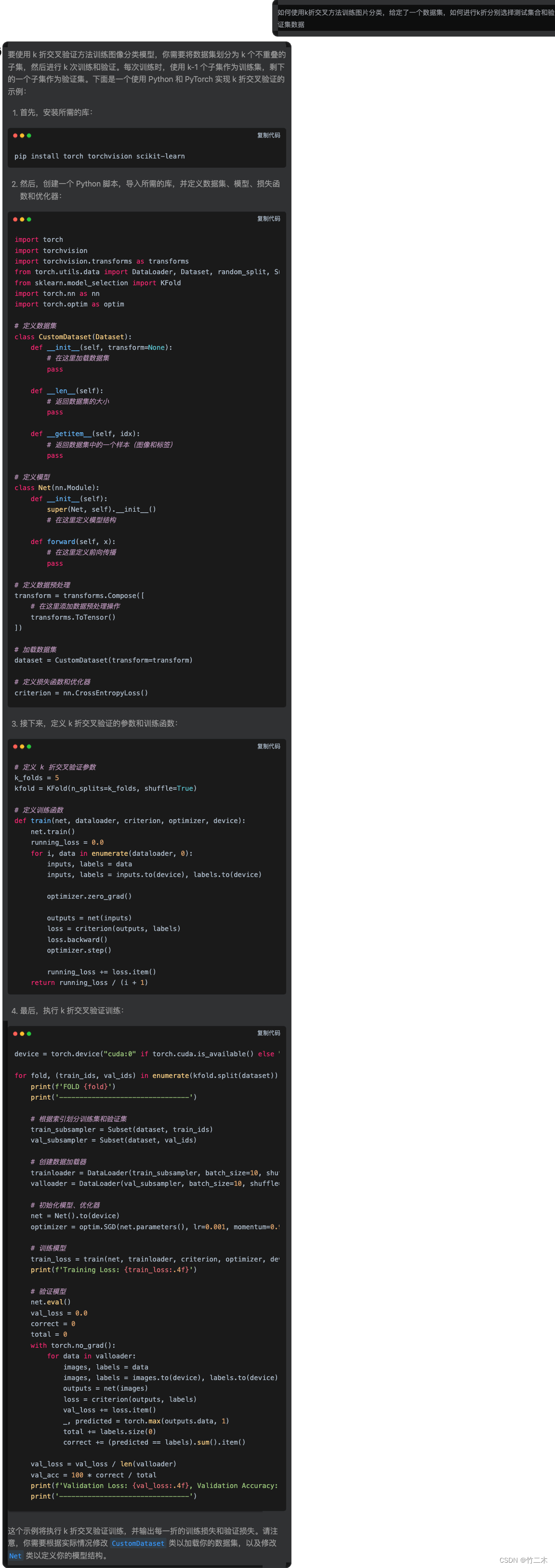
顾名思义，该算法不是通过比较数据的大小来进行排序的，而是通过统计数组中相同元素出现的次数，然后通过统计的结果将序列回收到原来的序列中。

动图展示：
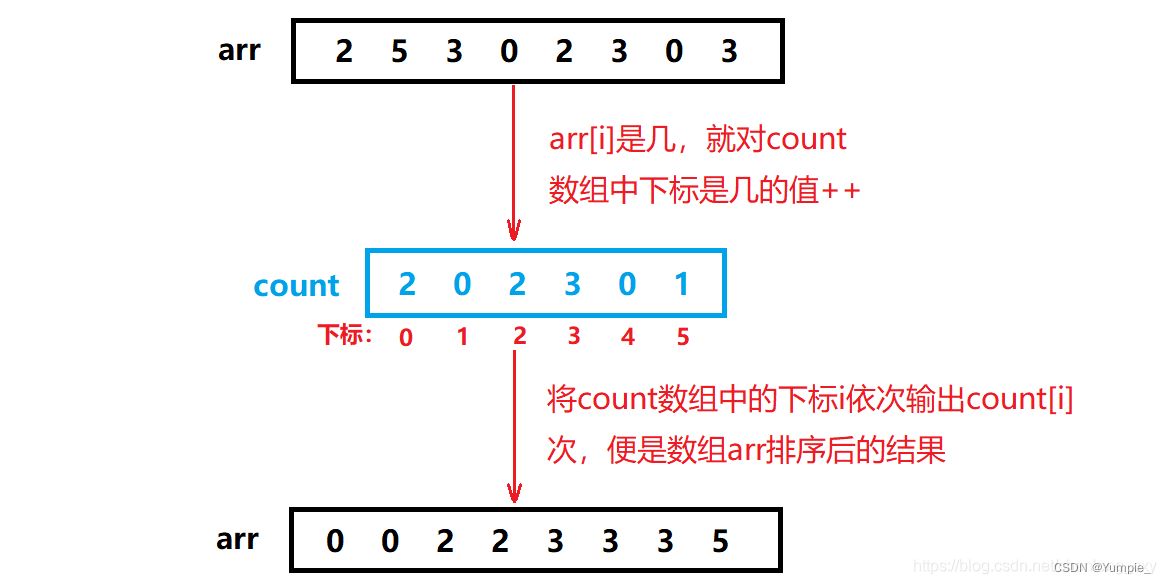
在这里插入图片描述

举个例子：
在这里插入图片描述

上列中的映射方法称为绝对映射，即arr数组中的元素是几就在count数组中下标为几的位置++，但这样会造成空间浪费。例如，我们要将数组：1020,1021,1018，进行排序，难道我们要开辟1022个整型空间吗？
若是使用计数排序，我们应该使用相对映射，简单来说，数组中的最小值就相对于count数组中的0下标，数组中的最大值就相对于count数组中的最后一个下标。这样，对于数组：1020,1021,1018，我们就只需要开辟用于储存4个整型的空间大小了，此时count数组中下标为i的位置记录的实际上是1018+i这个数出现的次数。

总结：
绝对映射：count数组中下标为i的位置记录的是arr数组中数字i出现的次数。
相对映射：count数组中下标为i的位置记录的是arr数组中数字min+i出现的次数。

计数排序算法过程

1 根据待排序集合中最大元素和最小元素的差值范围，申请额外空间；
2.遍历待排序集合，将每一个元素出现的次数记录到元素值对应的额外空间内；
3.对额外空间内数据进行计算，得出每一个元素的正确位置；
4.将待排序集合每一个元素移动到计算得出的正确位置上。

先假设 20 个数列为：{9, 3, 5, 4, 9, 1, 2, 7, 8，1，3, 6, 5, 3, 4, 0, 10, 9, 7, 9}。

让我们先遍历这个无序的随机数组，找出最大值为 10 和最小值为 0。这样我们对应的计数范围将是 0 ~ 10。然后每一个整数按照其值对号入座，对应数组下标的元素进行加1操作。

比如第一个整数是 9，那么数组下标为 9 的元素加 1，如下图所示。

在这里插入图片描述

第二个整数是 3，那么数组下标为 3 的元素加 1，如下图所示。

在这里插入图片描述

继续遍历数列并修改数组…。最终，数列遍历完毕时，数组的状态如下图。

在这里插入图片描述

数组中的每一个值，代表了数列中对应整数的出现次数。

有了这个统计结果，排序就很简单了，直接遍历数组，输出数组元素的下标值，元素的值是几，就输出几次。比如统计结果中的 1 为 2，就是数列中有 2 个 1 的意思。这样我们就得到最终排序好的结果。

0, 1, 1, 2, 3, 3, 3, 4, 4, 5, 5, 6, 7, 7, 8, 9, 9, 9, 9, 10

计数排序代码实现

代码示例:

//计数排序
void CountSort(int* a, int n)
{int min = a[0];//记录数组中的最小值int max = a[0];//记录数组中的最大值for (int i = 0; i < n; i++){if (a[i] < min)min = a[i];if (a[i] > max)max = a[i];}int range = max - min + 1;//min和max之间的自然数个数（包括min和max本身）int* count = (int*)calloc(range, sizeof(int));//开辟可储存range个整型的内存空间，并将内存空间置0if (count == NULL){printf("malloc fail\n");exit(-1);}//统计相同元素出现次数（相对映射）for (int i = 0; i < n; i++){count[a[i] - min]++;}int i = 0;//根据统计结果将序列回收到原来的序列中for (int j = 0; j < range; j++){while (count[j]--){a[i++] = j + min;}}free(count);//释放空间
}