原文链接
APR、
本篇论文是对抗训练在RS领域的先锋作,在这篇文章前对抗训练应用在图像领域,以提高模型鲁棒性。本篇论文填补了对抗训练在RS领域的空缺,首次基于BPR进行对抗训练,以提高RS排序模型的鲁棒性。
Motivation
文章在Session 2部分对MF的隐空间的扰动是否会造成推荐性能的下降,分析了BPR-MF是脆弱的。
首先在BPR-MF隐空间(不在输入进行扰动是因为,userID/itemID是离散的,扰动会变更其语义),即参数空间添加如下的扰动:
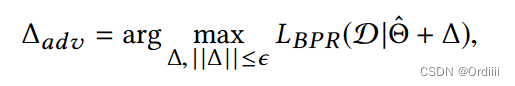
因为BPR的目标函数的非线性性质,求解最大值很棘手,于是文章借用FGSM的思想,近似目标函数为线性函数,近似扰动的最大值为:
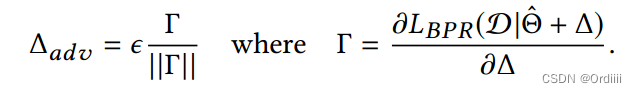
这里 Γ / ∣ ∣ Γ ∣ ∣ \Gamma/||\Gamma|| Γ/∣∣Γ∣∣表示的扰动的方向,而 ϵ \epsilon ϵ则控制扰动的大小,指的是直接沿着梯度的方向更新(在线性假设下)。
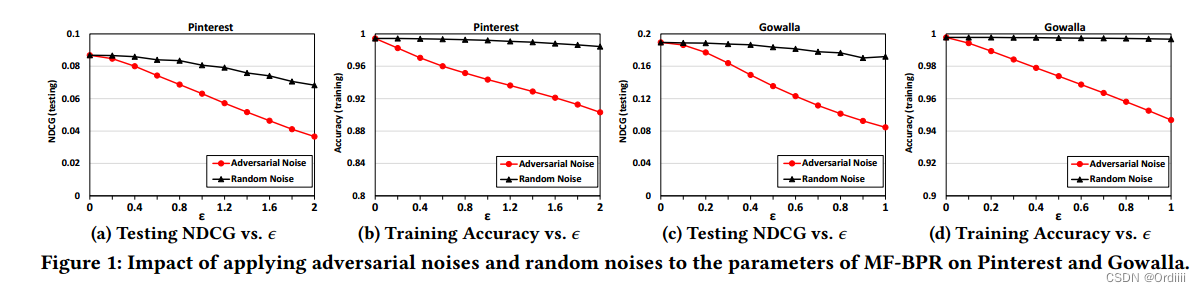
上图实验表明有针对设计的扰动确实比随机扰动会使得性能下降,说明了BPR-MF对训练数据过拟合,不具有鲁棒性。为了解决这个问题,作者提出了APR,即Adversarial Personalized Ranking模型。
Contributions
- 分析了BPR模型对扰动敏感,不具有鲁棒性,训练较好的BPR模型过拟合
- 提出了APR框架,即在RS领域的对抗训练
APR
APR的目标函数如下: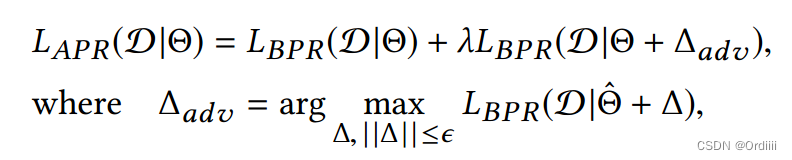
为了训练鲁棒的排序模型,目标函数首先最大化扰动,使得扰动对模型的破坏最大,然后在普通的BPR loss上加上对样本进行扰动过后的BPR loss,其中 λ \lambda λ 超参数衡量两部分的比例。从而最小化该目标函数使得在具有一般样本及扰动样本的情况下训练模型,其中扰动项可以视为一种正则化项,防止模型的过拟合。这本质上是一种minimax game:
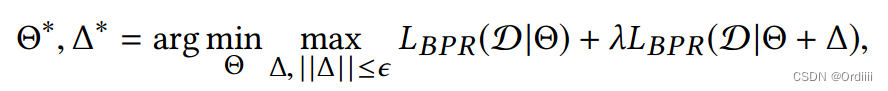
下面逐项分析
Δ \Delta Δ 最大值
BPR带上扰动的损失函数为:
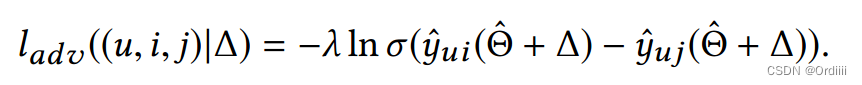 因为许多模型,例如bilinear MF以及MLP都是非线性的,因此直接求出 Δ \Delta Δ最大值较为棘手,因此根据Motivation部分的分析, Δ \Delta Δ最大值近似为:
因为许多模型,例如bilinear MF以及MLP都是非线性的,因此直接求出 Δ \Delta Δ最大值较为棘手,因此根据Motivation部分的分析, Δ \Delta Δ最大值近似为:
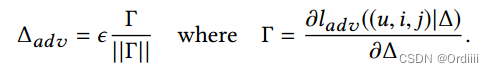
其中:
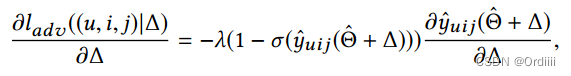
模型参数 Θ \Theta Θ最小
因此,APR(基于BPR)的目标函数为:
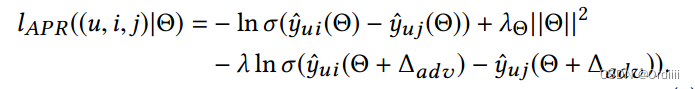
利用SGD进行更新即为:
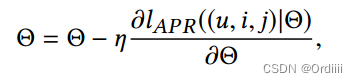
其中:
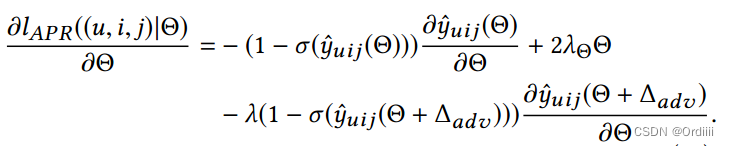
注意,在训练过程中BPR的初始化因为训练好的BPR,因为只有在BPR过拟合的情况下,添加扰动才是合理的,因此参数 Θ \Theta Θ可以从预训练模型中取得。
APR实例,基于MF的APR(AMF)
即在MF模型上使用APR框架,模型结构如下所示:
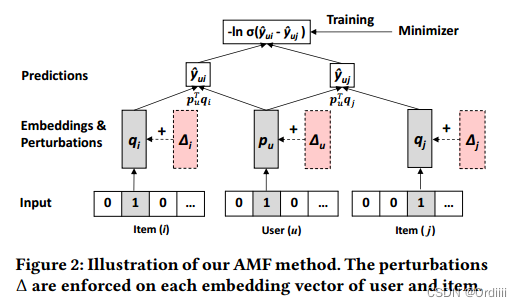
其中目标函数以及梯度可以按照APR框架得到,这里省略,有兴趣可以参考原文。
EXPERIMENTS
数据集
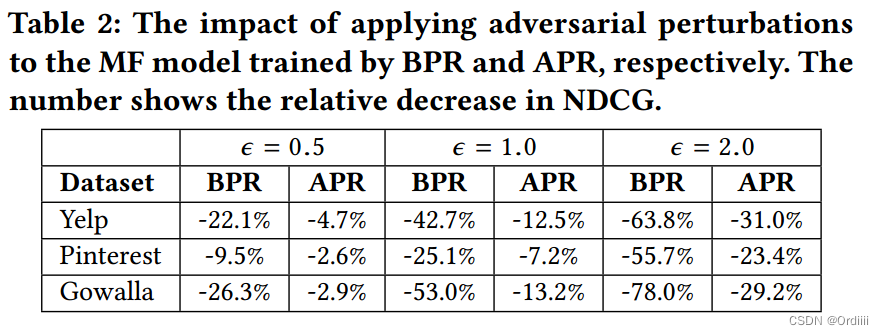
实验部分文章主要介绍了
- HR,NDCG随着epoch增加变化的表现
- 不同embedding size对应的指标大小
- 与baseline的对比实验
- 以及扰动参数 ϵ \epsilon ϵ和扰动项权重 λ \lambda λ不同大小的实验
详细可以参考原文
总结与思考
这篇文章提出了一个在RS领域应用对抗训练提高模型的鲁棒性。
在阅读文章过程中我有几点问题/想法
- 目标函数是minmax game,那么是否可以用GAN的方法来同时更新扰动 Δ \Delta Δ以及 Θ \Theta Θ,即训练 Δ \Delta Δ使得模型尽可能差,同时训练 Θ \Theta Θ使得模型尽可能抵抗这种扰动
- 这篇文章的扰动仅仅是在浅层,是否可以对更加深层次扰动,效果会不会更好?