文章目录
- 前言
- 索引结构及查找算法
- 不适合做MySql的数据结构及其原因
- 一、BTree和B+Tree的引出
- 1.1 BTree数据结构
- 2.2 B+Tree数据结构
- 二、计算m阶,即B+Tree该取多少合适
- 总结
前言
索引结构及查找算法
一个sql语句在mysql里究竟是如何运行的呢?又是怎么去查找的呢?其中就涉及到数据库(存储数据)以及查找算法。先来看一下几种查找算法;
- 目录查找:类似索引
- 遍历:暴力查找
- 二分:B+树的基础算法
- 键查找:hash查找
能做索引的数据结构有:数组、链表、红黑树、B树(B-树、B+树)。
那么哪种数据结构适合做 MySql 数据库的存储结构呢?
先来说下数据的一般存储方式:内存(适合小数据量)、磁盘(大数据量)。
磁盘的运转方式:速度 + 旋转,磁盘页的概念:每一页大概16KB。
不适合做MySql的数据结构及其原因
数组和链表的缺点就是数据量大的时候存不了,也就是说不合适大数据量。
哈希是通过hash函数计算出一个hash值的,存在哈希碰撞的情况,另外哈希也不支持部分索引查询以及范围查找。但是哈希的优点就是查找的时间复杂度是O(1),那么什么情况下可以使用hash索引呢?就是查询条件不会变,而且没有部分查询和范围查询的时候。
红黑树存储的数据量大的时候,红黑树的节点层数多,也就是树的高度比较高,查找的底层数据时,查找次数就比较多,即对磁盘IO使用比较频繁。总结为以下两点:
- 读取浪费太多:通过计算本来树的每一层大概需要分配16KB的数据,但是对于红黑树来说,实际存的节点数比较少,即存的数据大小远远小于16KB,从而造成存储空间的浪费
- 读取磁盘的次数过多:树的层数越多,查找数据时读取磁盘的次数也就越多
如下图所示,如果需要查找数字4的话,需要查找三次,即对磁盘IO操作三次:
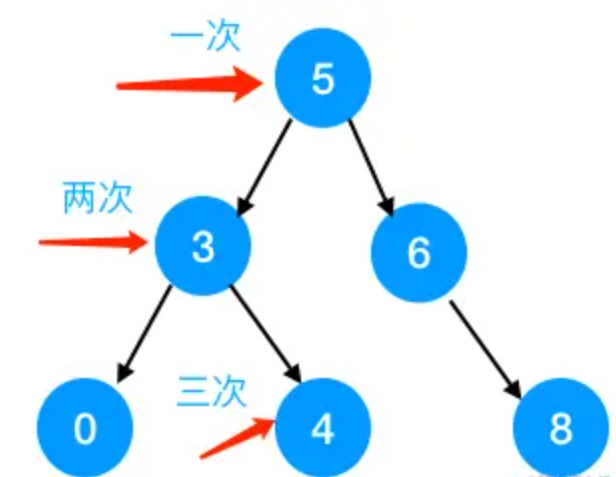
我们想下,那为什么红黑树又可以在hashMap的查找那里用呢?
这就涉及到磁盘和内存的区别了,这里就不展开解释了,只需要知道是因为hashMap使用到是内存就可以了。
一、BTree和B+Tree的引出
针对红黑树以上总结的两点(不适合用来做mysql的数据结构的原因),有什么可以改进的方法呢?我们可以从以下两点出发:
- 增加树每层的节点数量,这样可以对分配的16KB充分利用,即解决上面的读取浪费的问题
- 尽可能的让树的高度减小,使得树显得比较“矮胖”,这样可以减少读取磁盘的次数
那么怎么样才可以实现以上的方法呢?这就需要用到B+树了,实际上MySql的底层数据结构就是用的B+树。
1.1 BTree数据结构
N阶的BTree的几个重要特性:
- 节点最多含有N颗子树(指针),N-1个关键字(数据存储空间) (N>=2);
- 除了根节点和叶子节点外,其它每个节点至少有M=N/2个子节点,M向上取整,即分裂的时候从中间分开,分成M棵子树;
- 若根节点不是叶子结点,则至少有两颗子树。
什么意思呢,我们来看下面这颗三阶的B树,结构大概长这样:
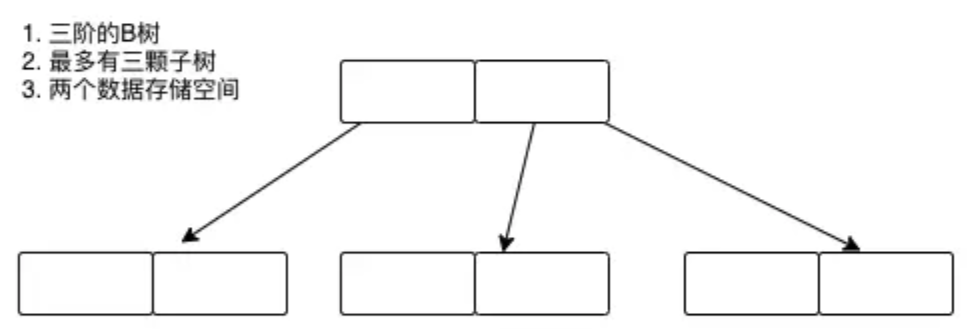
BTree有一个非常重要的操作,当一颗树不满足以上的性质的时候,会进行怎样的操作?红黑色大家已经知道了会进行变换颜色、左旋或右旋操作。而BTree会进行分裂操作。
先来看个例子:
创建一棵5阶的BTree,插入的数据有:2,13,6,1,7,4,10,12,5,16,22。
根据BTree的特性,5阶则在磁盘的页中最多有5个指针(存储查找路径的地址)、4个存储空间(存储关键字,即需要存的数据),那么具体的插入数据如下所示:
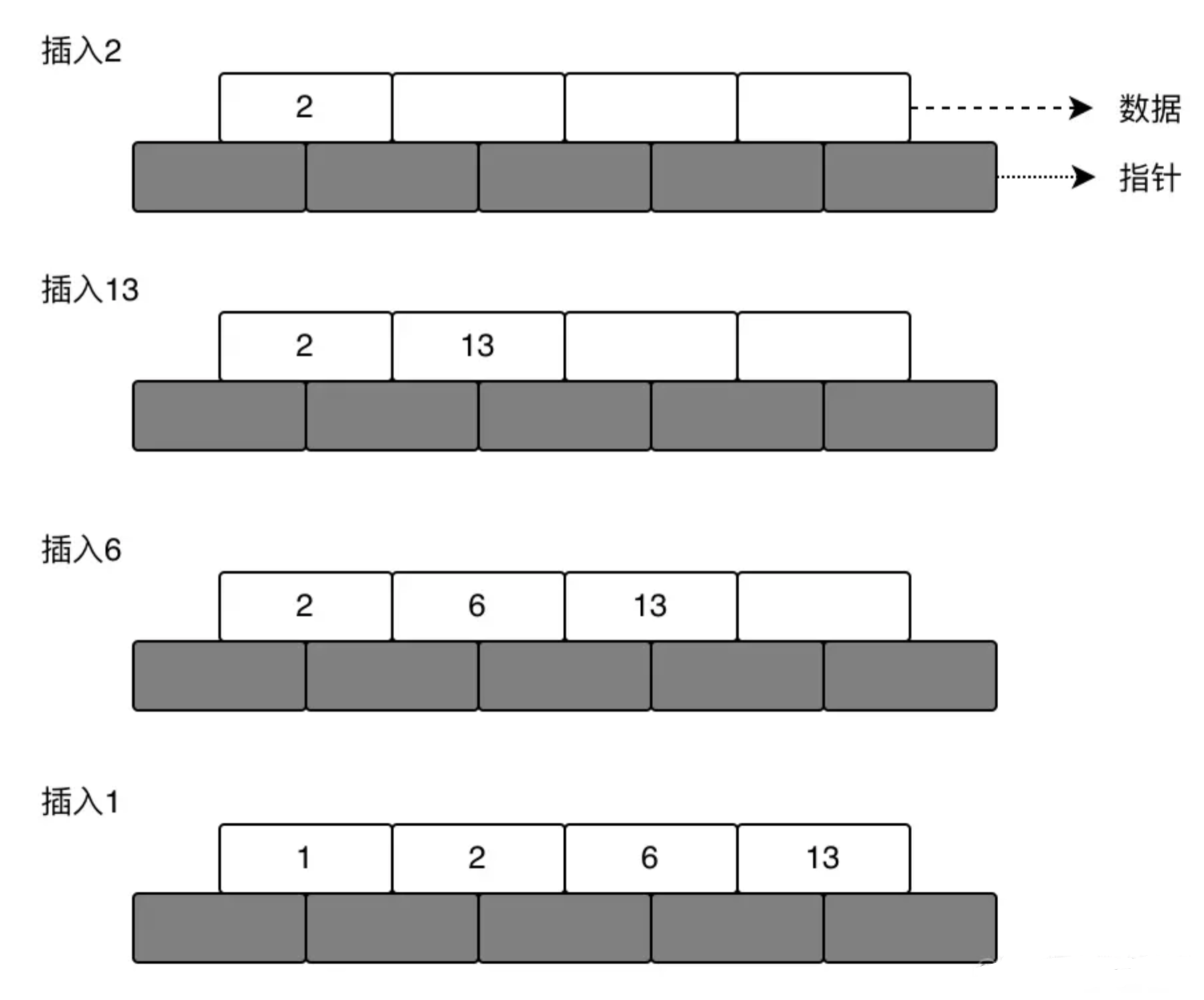
当插入7的时候,发现空间不足,此时就会出现分裂操作,从中间节点分开,把中间节点移到根节点,如下:
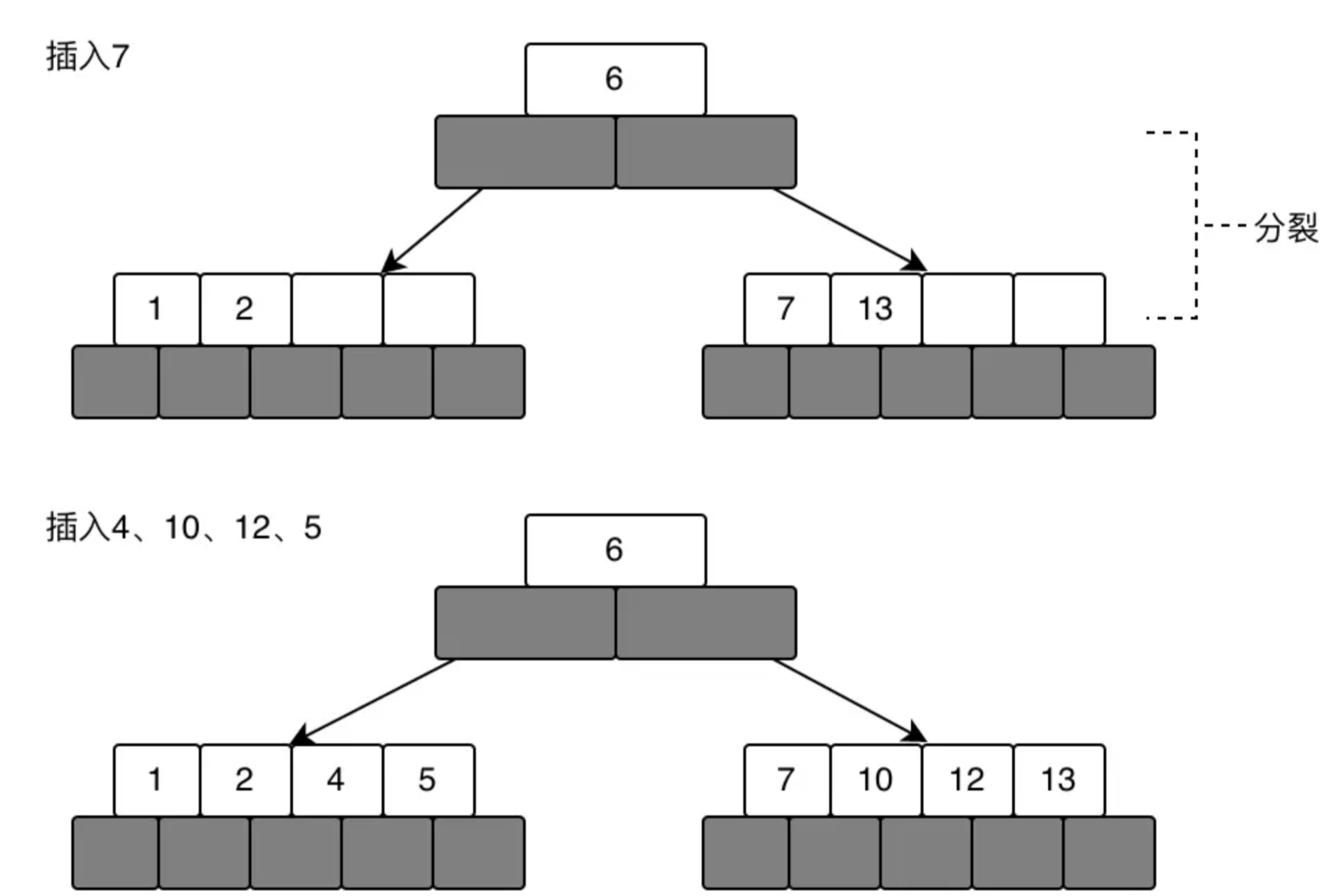
当插入16的时候,比6大,应该插入到右子树13的右边的,但是发现的空间不够,此时又会进行分裂操作,从右子树的中间节点(12)分开,把中间节点移到根节点,然后分裂成左右子树,这时一共有三颗子树了,如下所示:
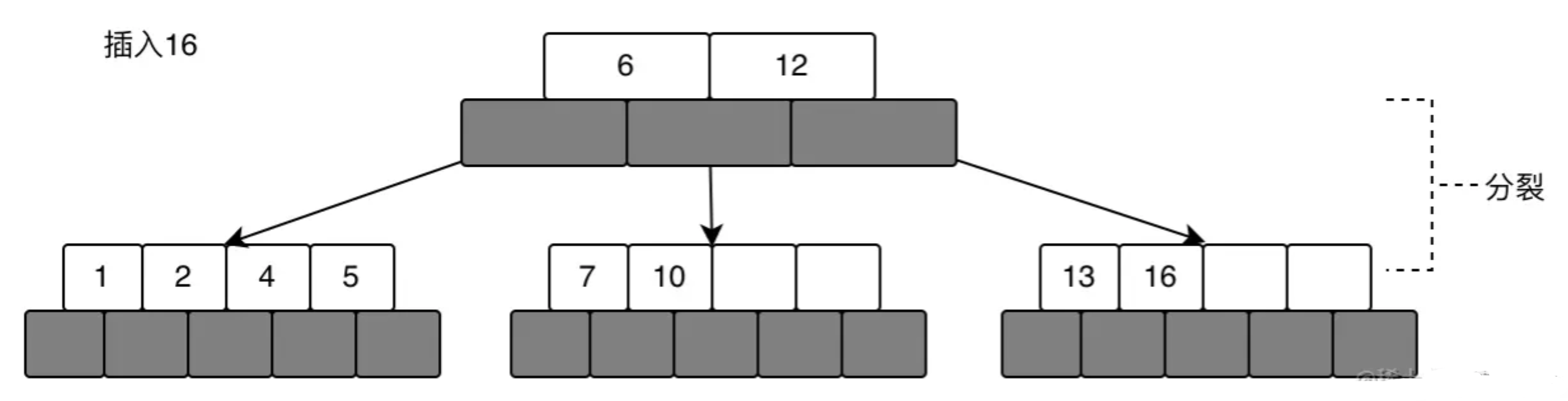
最后插入22得到的一颗完整的树如下:
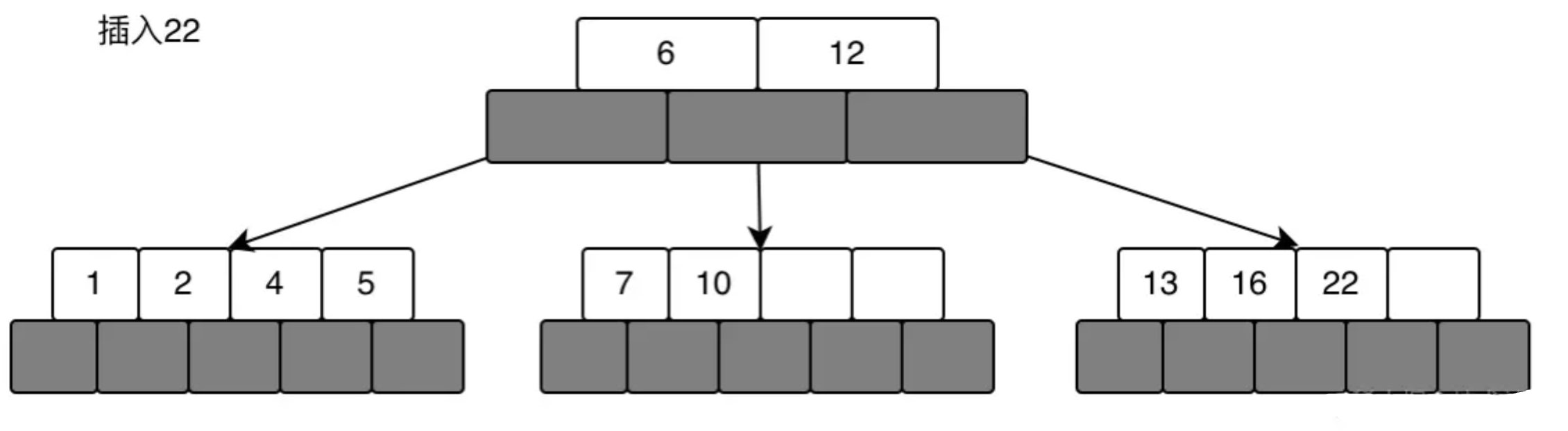
大家也可以添加多其它数据,然后看看分裂后的效果,这里就不一一列举了。
需要注意的是:分裂后的树节点仍要满足BTree的特性,其实也是满足二叉查找树(二叉排序树)的特点。
可以看到左子树的值比6小,中间节点的值(7、10)介于6和12之间,右子树的值均比12大。总的来说就是从左到右是有序的。
以上操作是BTree构建的详细过程,需要注意的是在构建过程中进行分裂的操作,分裂后必须关注的是是否仍满足了BTree的特性,是否是一颗二叉排序树。有时候插入一个数时,可能会经过多次分裂操作。
回过头来看上面提到的两个问题:
- 读取浪费太多;
- 磁盘读取次数过多。
根据BTree的特点,我们可以看到BTree的查找效率还是挺高的,也能够解决这两个问题。
但是MySql还是没有选择使用BTree数据结构,这是为什么呢?主要原因有以下这几点:
- 因为BTree不适合范围查找。就拿上面的来举例,比如我要查找小于6的数据,则先找到6的节点,然后需要遍历一遍6节点(索引)的左子树,不遍历的话,就拿不到小于6的这些数据了,也就说索引失效了,所以说不适合范围查找。
- BTree的节点除了存储索引之外,还存储了数据本身,占用空间较大,但是磁盘的页大小是有限的(16KB左右),因此,存储同样大小的数据,BTree显得比较高(相对B+Tree),稳定性弱一些。
综上两个主要原因,MySql最终选择了B+Tree的数据结构来存储数据。
2.2 B+Tree数据结构
B+Tree和BTree的分裂过程类似,只是B+Tree的非叶子节点不会存储数据,只存储索引值(指针地址),所有的数据都是存储在叶子节点,其目的是为了增加系统的稳定性。这里就不再列举B+Tree的分裂过程了,我们直接看下B+Tree到底长啥样,如下图所示:
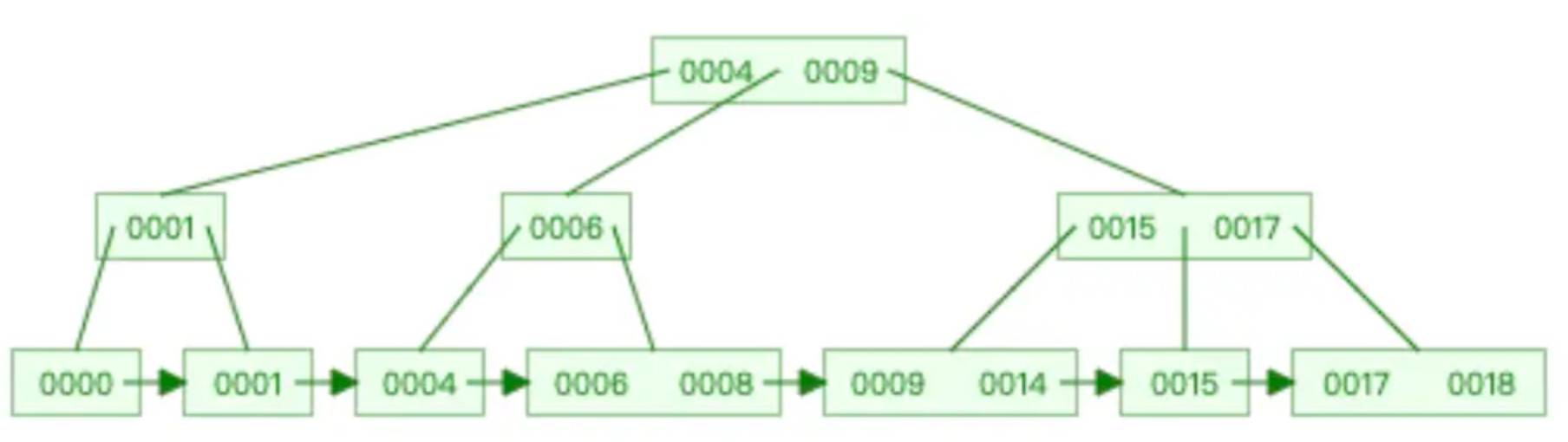
实际上MySql的底层数据结构B+Tree是长这样的,如下图所示:
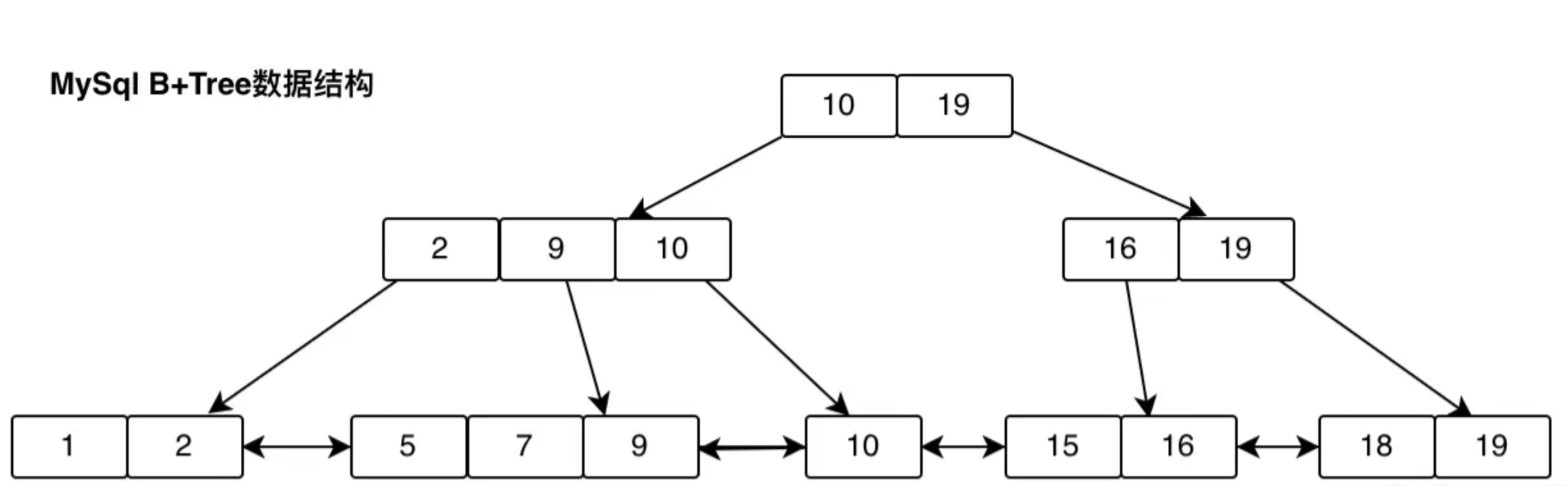
大家可以看出B+Tree与BTree有啥不一样呢?由上图可以看出B+Tree有以下几个特点:
- 叶子节点连起来了,是一条有序的双向链表,目的是为了解决范围查找。比如需要查找小于9的数据,只要找到等于9的数据,然后将9的左边数据全部拿出来即可。
- 非叶子节点不存数据,只存索引,空间利用更高效。
- 数据的个数和节点一样多,换句话说,非叶子节点存的是其子树的最大或最小值。
对于索引失效的情况,BTree是需要遍历整棵树才能把所有数据拿到,而B+Tree只需要找到叶子节点的第一个节点即可把所有数据拿到,可见效率是B+Tree更优,这就是双向链表的妙用。
二、计算m阶,即B+Tree该取多少合适
m是怎么计算出来的呢?是根据磁盘的页大小来计算的,也就是说是由磁盘页大小决定的。
我们知道,磁盘的页大小大概是16K,MySql创建索引时,可以根据字段及类型来计算磁盘一页大概可以存多少数据。
根据官方文档描述,树高度等于2时(2阶),大概可以存两万多条数据;高度等于3时(3阶),大概可以存两千多万条数据,怎么计算的呢?
首先,1 千字节(KB)=1024 字节(B),一页有16KB,假设存主键+指针大概有8+6=14B,则一页就可以存:16*1024/(8+6)=1170 个索引了。
对于3阶的B+Tree来说,大概可以存:1170^3 条数据,大概是两千万。
总结
BTree是B+Tree的一个过渡,B+Tree适合用于大数据量的磁盘索引数,经典的就是上面讲到的作为MySql的底层索引结构,所有的数据都存在叶子节点,其它节点只存储索引,增加了系统的稳定性、提高查找效率以及查询时减少磁盘的IO操作。