浙江大学版《概率论与梳理统计》一书中的,第13章第1节例2如下:

这个解释和模型比较简单易懂。接下来,第2节的例2是一个关于此模型的题目:

在我自己的理解中,此题的解法跟上一个题目一样,第二级传输后,一共有4中可能性,按照平均概率相加即可。
{ p n q n q n p n } \begin {Bmatrix} p^n & q^n \\ q^n & p^n \end{Bmatrix} {pnqnqnpn}
然而,仔细考虑之后发现不妥。因为最后结果的概率,这样计算不太合适,但是又没有发现更合理的理论和方法,又看到这一节的如下论述:


似乎抓到了什么,但是又特别模糊。
再看以下C-K方程:

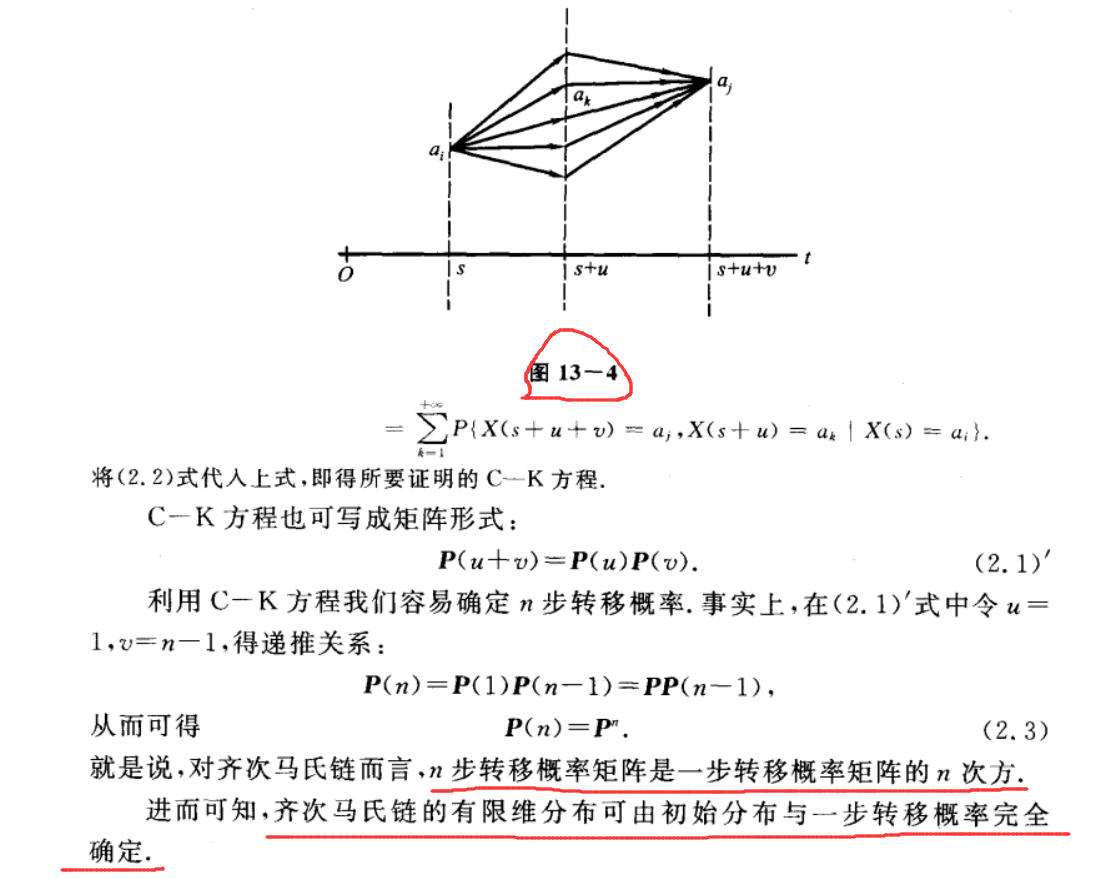
因此,参考此文:https://blog.csdn.net/m0_37567738/article/details/132182007?spm=1001.2014.3001.5502可以得出结论,此种题目的解题方法还是要回到马尔可夫概率转移矩阵中去找答案。
我觉得要理解此题目的底层逻辑,还需要了解以下公式:
P { X n = a n } = ∑ i = 1 + ∞ P { X n = a n , X 0 = a i } = ∑ i = 1 + ∞ P { X n = a n ∣ X 0 = a i } P { X 0 = a i } = ∑ i = 1 + ∞ P i ( 0 ) P i j ( n ) = ∑ i = 1 + ∞ P i 1 ( 1 ) P i j ( n − 1 ) = ∑ i = 1 + ∞ P 2 i ( 2 ) P i j ( n − 2 ) = ∑ i = 1 + ∞ P 3 i ( 3 ) P i j ( n − 3 ) = . . . . . . P \{X_n = a_n\} = \sum_{i = 1}^{+\infty} P\{ X_n = a_n, X_0 = a_i \} = \\ \sum_{i = 1}^{+\infty} P\{ X_n = a_n|X_0 = a_i \} P\{ X_0 = a_i \}=\sum_{i=1}^{+\infty} P_i(0) P_{ij}(n) = \\ \sum_{i=1}^{+\infty} P_{i1}(1) P_{ij}(n-1)= \sum_{i=1}^{+\infty} P_{2i}(2) P_{ij}(n-2) = \sum_{i=1}^{+\infty} P_{3i}(3) P_{ij}(n-3) = ...... \\ P{Xn=an}=i=1∑+∞P{Xn=an,X0=ai}=i=1∑+∞P{Xn=an∣X0=ai}P{X0=ai}=i=1∑+∞Pi(0)Pij(n)=i=1∑+∞Pi1(1)Pij(n−1)=i=1∑+∞P2i(2)Pij(n−2)=i=1∑+∞P3i(3)Pij(n−3)=......
这个逻辑的本质区别就在于,它是利用后验概率去推算先验概率的,这是一种理论上的优越性。
我们想要求解的概率P,它依赖于其概率矩阵的乘法运算,而不是说简单把4种转换相加。