prim算法简介

$Prim$算法是一种用于解决最小生成树问题的贪心算法。最小生成树是一个连通图的生成树，它的所有边的权重之和最小。

prim算法步骤

以下是$Prim$算法的详细步骤：

当$Prim$算法执行时，可以使用以下数据结构来辅助实现：

一个优先队列（最小堆）：用于存储与当前最小生成树集合相连的边，并按照权重进行排序。
一个布尔数组$visited$：用于标记顶点是否已经被访问过。
以下是$Prim$算法的详细步骤：

初始化一个空的最小生成树集合$MST$和一个空的顶点集合$visited$。
选择一个任意顶点作为起始点，并将其加入$visited$集合。
对于起始点的所有相邻边，将它们加入优先队列。
重复以下步骤，直到$visited$集合包含所有顶点：

1. 从优先队列中取出权重最小的边$e$，并将其另一个顶点$v$加入$visited$集合。

2. 如果$v$已经被访问过，则跳过该边。

3. 将边$e$加入$MST$集合。

4. 对于顶点$v$的所有相邻边，如果另一个顶点不在$visited$集合中，则将这些边加入优先队列。返回$MST$集合作为最小生成树。

在$Prim$算法的执行过程中，优先队列的作用是选择与当前最小生成树集合相连的权重最小的边。这样可以保证每次选择的边都是当前最小生成树集合与其他顶点之间的最短边。

prim复杂度

$Prim$算法的时间复杂度取决于优先队列的实现方式。如果使用二叉堆实现优先队列，时间复杂度为$O(E$ $logV)$。

prim样例题目

公路修建

题目描述

某国有 $n$ 个城市，它们互相之间没有公路相通，因此交通十分不便。为解决这一“行路难”的问题，政府决定修建公路。修建公路的任务由各城市共同完成。

修建工程分若干轮完成。在每一轮中，每个城市选择一个与它最近的城市，申请修建通往该城市的公路。政府负责审批这些申请以决定是否同意修建。

政府审批的规则如下：

1. 如果两个或以上城市申请修建同一条公路，则让它们共同修建；
2. 如果三个或以上的城市申请修建的公路成环。如下图，A 申请修建公路 AB，B 申请修建公路 BC，C 申请修建公路 CA。则政府将否决其中最短的一条公路的修建申请；
3. 其他情况的申请一律同意。

一轮修建结束后，可能会有若干城市可以通过公路直接或间接相连。这些可以互相连通的城市即组成“城市联盟”。在下一轮修建中，每个“城市联盟”将被看作一个城市，发挥一个城市的作用。

当所有城市被组合成一个“城市联盟”时，修建工程也就完成了。

你的任务是根据城市的分布和前面讲到的规则，计算出将要修建的公路总长度。

输入格式

第一行一个整数 $n$，表示城市的数量。（$n\le 5000$）

以下 $n$ 行，每行两个整数 $x$ 和 $y$，表示一个城市的坐标。（$-10^6\le x,y\le 10^6$）

输出格式

一个实数，四舍五入保留两位小数，表示公路总长。（保证有惟一解）

样例

样例输入

4
0 0
1 2
-1 2
0 4

样例输出

6.47

提示

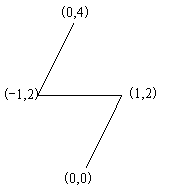
修建的公路如图所示：

prim样例代码

上题的正解：

#include <bits/stdc++.h>
using namespace std;
const int N=10000;
struct city { double x,y; } node[N];
double ans,minn,dis[N];
int n,m,k,now;
bool ff[N];
double far(double x1,double y1,double x2,double y2) {return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
int main() {cin >>n;for (int i=1; i<=n; i++) {cin >>node[i].x >>node[i].y;dis[i]=0x7fffffff;}dis[1]=0; ff[1]=1;for (int i=1; i<=n; i++) {minn=0x7fffffff;now=1;for (int j=2; j<=n; j++) {if (!ff[j] && dis[j]<minn) {now=j;minn=dis[j];}}ff[now]=1;ans+=dis[now];for (int j=1; j<=n; j++) {dis[j]=min(dis[j],far(node[now].x,node[now].y,node[j].x,node[j].y));}}printf("%.2lf",ans);return 0;
}