(一)八皇后问题描述
在一个8x8的棋盘上放置8个皇后,使得每个皇后都不会互相攻击,即任意两个皇后都不能在同一行、同一列或同一条对角线上。
(二)算法思路
由于八皇后问题的解法数量较多,本文将介绍其中一种解法——回溯法。
1.回溯法是一种通过遍历所有可能的解来寻找所有的解的算法。
如果一个候选解被发现不可能是一个正确的解,回溯算法会舍弃它,从而在候选解空间树中减少搜索的范围。
PS:区别穷举法?
在于进行搜索范围的优化吖!及时止损~
2.使用一个一维数组来表示每个皇后的位置。
PS:为什么不用二维数组a[i][j]进行行和列的表示呢?
答:观察发现:每个皇后是不是分别占据了一层城堡,也就是从0一直到n-1行,每一行安排一个皇后的嘛,是不是了啦~
数组的下标代表皇后所在的行数,数组的值代表皇后所在的列数。
3.具体的解题思路如下:
从第一行开始放置皇后。
逐行放置皇后,直到最后一行。
在每一行中,逐个尝试放置皇后。
如果当前位置可以放置皇后,将皇后的位置记录在数组中,并进入下一行。
如果当前位置无法放置皇后,回溯到上一行,重新尝试放置皇后。
如果所有行都放置了皇后,输出解法。
PS:咦?问题又来了,这个皇后得把她们安排多少个超级大循环才可以给皇后一个家呢?
答:不知道要尝试多少次呀!那就直接while(1)呗!
(三)回溯算法整个代码的超级详细分析
以下是使用回溯法解决八皇后问题的C语言代码:
1.变量&函数:
变量名 | 变量类型 | 作用 |
queen | int[N] | 用于记录每个皇后所在的列数 |
count | int | 解法总数 |
函数名 | 参数 | 作用 |
check | int rowint col | 判断当前位置是否可以放置皇后,如果可以则返回1,否则返回0。 |
backtrack | int row | 回溯到上一行,并重新尝试放置皇后 |
main | 无 | 返回int,调用backtrack函数求解八皇后问题,最终输出解法总数。 |
int queen[N] = {0}; // 用于记录每个皇后所在的列数
int count = 0; // 解法总数
int check(int row, int col) {}
void backtrack(int row) {}
int main() {}
2.皇后棋盘摆放0 or 1👉check
遍历一行中的每一个空,当前位置同一列或同一对角线上已经有皇后,返回0,否则返回1:
if (queen[i] == col ||
row - i == col - queen[i] ||
row - i == queen[i] - col) {
return 0;
}
🐱🐉不同行:i表示行,queen[i]表示列,一行一个循环
🐱🐉同列:queen[i]==col
🐱🐉正对角线+反对角线:
-
左下方:row-i==col-queen[i]
-
右下方:row-i==queen[i]-col
3.回溯算法核心在此👉backtrack
输入参数:当前行数row(当前正在尝试放置皇后的行数)
PS:还是看不懂咋回溯嘛
从第1行开始,放置成功后再递归到下一行继续放置
如果在某一行中无法放置皇后,我们就需要回溯到上一行重新尝试其他位置。
🐱🐉当前行数等于N→找到了一种解法,解法总数count加1,直接返回,结束当前的递归。
PS:可不可以再详细一点
答:当我们成功地在第8行放置皇后后,说明我们已经找到了一种解法,此时我们可以将解法总数加1,并结束当前的递归,如下:
if (row == N) { // 找到了一个解法
count++;
return;
}
🐱🐉当前行数不等于N→在当前行上尝试放置皇后。
-
for循环遍历当前行的每个位置
②每个位置(i,j)→调用函数check来判断是否可以放置皇后。
是:将该皇后的列数j记录在数组queen中的第row个位置上。
③递归调用backtrack函数,尝试在下一行放置皇后。
在递归调用完成后,我们需要回溯到上一行,并将之前记录的皇后位置清空,以便重新尝试其他可能的解法。
for (int i = 0; i < N; i++) { // 尝试在当前行的每个位置上放置皇后
if (check(row, i)) {
queen[row] = i;
backtrack(row + 1);
queen[row] = 0;
}
}
PS:更详细些
首先,使用for循环遍历当前行的每个位置,即从0到N-1,对于每个位置i,执行以下操作:
调用函数check(row, i)判断当前位置是否可以放置皇后。如果可以放置,就执行以下操作:
将当前皇后的列数i记录在数组queen中的第row个位置上,表示在当前行的第i列放置了皇后。
递归调用函数backtrack(row + 1),表示在下一行尝试放置皇后。
在递归完成后,需要回溯到上一行,并将之前记录的皇后位置清空,以便重新尝试其他可能的解法。具体来说,将queen[row]的值置为0,表示该行没有放置皇后。
当for循环执行完毕后,函数backtrack返回,结束当前的递归。
通过这段代码,我们可以在每个可行的位置上递归调用函数backtrack,不断地尝试放置皇后,直到找到所有的解法。在递归过程中,我们使用数组queen来记录每个皇后所在的列数,以便在回溯时清空之前记录的位置。函数check用于判断当前位置是否可以放置皇后,从而帮助我们进行决策。通过这些函数和代码的组合,我们可以有效地解决八皇后问题。
(四)C语言代码呈上
第一种运行结果:

#include <stdio.h>
#define N 8
int queen[N] = {0}; // 用于记录每个皇后所在的列数
int count = 0; // 解法总数
int check(int row, int col) {for (int i = 0; i < row; i++) {// 如果当前位置同一列或同一对角线上已经有皇后,返回 0if (queen[i] == col || row - i == col - queen[i] || row - i == queen[i] - col) {return 0;}}return 1;
}
void backtrack(int row) {if (row == N) { // 找到了一个解法count++;return;}for (int i = 0; i < N; i++) { // 尝试在当前行的每个位置上放置皇后if (check(row, i)) {queen[row] = i;backtrack(row + 1);queen[row] = 0;}}
}
int main() {backtrack(0); // 从第一行开始尝试放置皇后printf("%d", count);return 0;
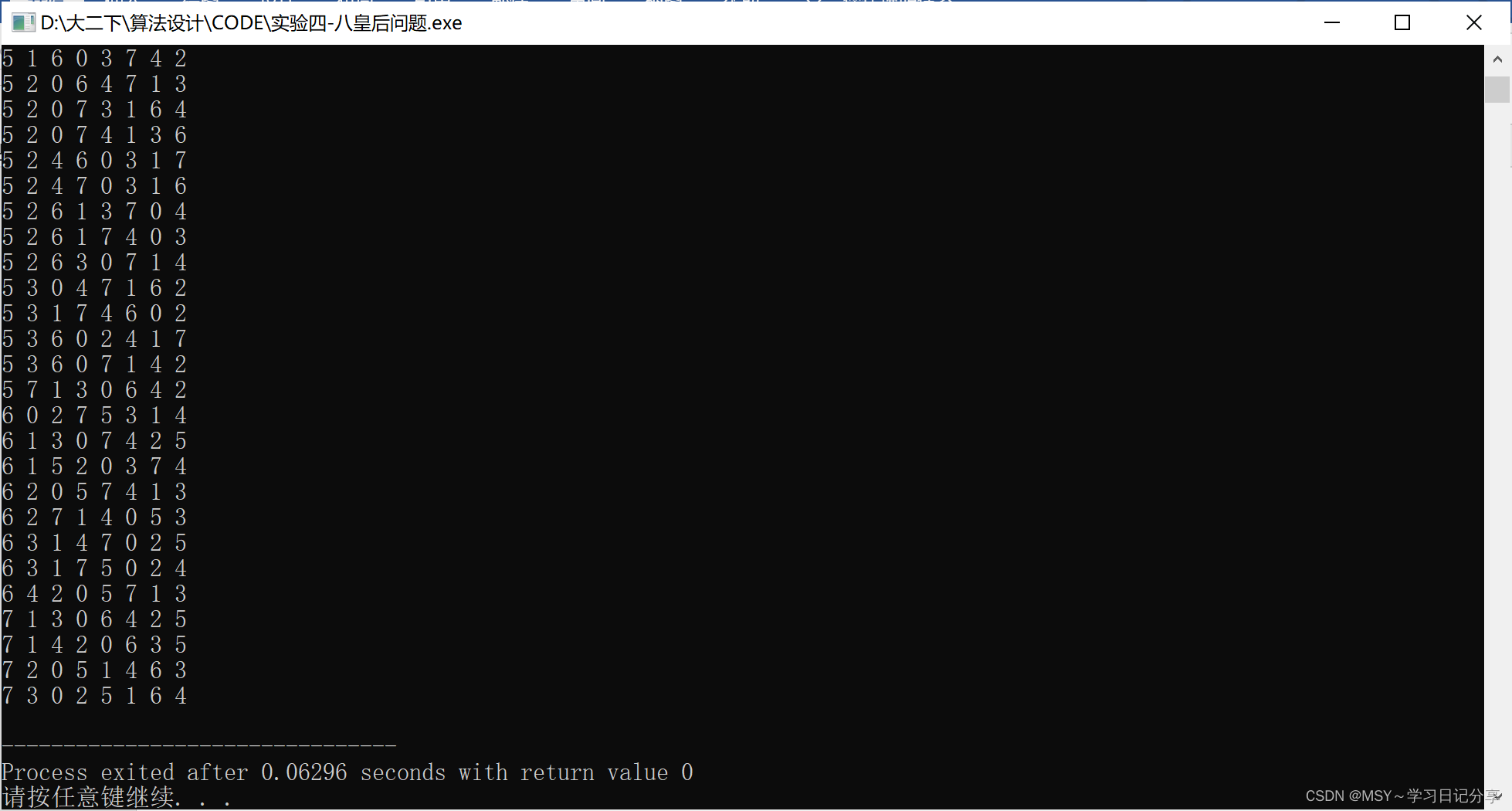
}第二种运行结果:
#include <stdio.h>
#define N 8
int queen[N] = {0}; // 用于记录每个皇后所在的列数
int check(int row, int col) {for (int i = 0; i < row; i++) {// 如果当前位置同一列或同一对角线上已经有皇后,返回 0if (queen[i] == col || row - i == col - queen[i] || row - i == queen[i] - col) {return 0;}}return 1;
}
void backtrack(int row) {if (row == N) { // 找到了一个解法for (int i = 0; i < N; i++) {printf("%d ", queen[i]);}printf("\n");return;}for (int i = 0; i < N; i++) { // 尝试在当前行的每个位置上放置皇后if (check(row, i)) {queen[row] = i;backtrack(row + 1);queen[row] = 0;}}
}
int main() {backtrack(0); // 从第一行开始尝试放置皇后return 0;
}