上节课讲了向量子空间中的列空间和零空间,这节课来讲零空间的(Special solutions)特解,也就是Ax=0的特解。在求解特解的核心便是使用消元法求得(row echelon form)阶梯矩阵或者(reduced row echelon form/RREF)最简矩阵。
我们接下来举一个例子,例如我们拥有如下的方程组Ax=0,我们将求解所有的x,即对矩阵A进行求解,注意到A是三个方程/三个约束条件,四个变量/四个自由度,

我们使用(elimination)消元法对矩阵进行化简(只用行变换),
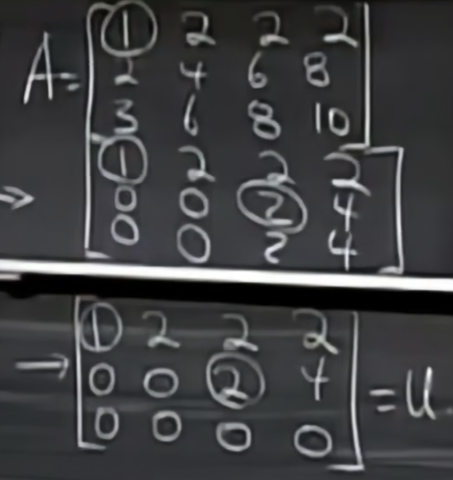
化为阶梯矩阵。阶梯矩阵的行数叫做这个矩阵A的(rank)秩,阶梯矩阵每一行中从左往右第一个不为0的元素叫做(pivots)主元,所在列叫做(pivot columns)主列,阶梯矩阵中除了主列外的列叫做(free columns)自由列。通过观察能够发现,整个矩阵的所有自由列都能够用主列线性表出。主元已经在上图中标出,为1,2。
那么如何求得Ax=0的特解呢,即如何求得矩阵A列分后的线性表出系数?我们常常采用将自由列赋予单位方向向量,例如有两个自由列就给自由列赋予[0, 1]和[1, 0],三个自由列就赋予[0, 0, 1], [0, 1, 0], [1, 0, 0]。如题目中我们赋予x2=1,x4=0。

再将自由量赋予特定值后,如x2=1,x4=0,我们对矩阵或者方程组进行回代,算出主列的系数x1和x3。
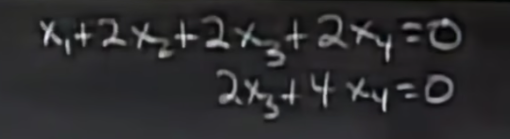
同理,我们再求x2=0,x4=1的线性表出系数,得到第二个解。这两个线性无关的解的所有线性组合就是Ax=0的特解,即x=c [-2, 1, 0, 0] + k [2, 0, -2, 1]。

通过经验能够发现,如果一个方程组是m*n的,即m个方程,n个未知量,且秩为r,则特解中所需的向量无关的向量个数为n-r。