算法原理:
Q ( s , a ; θ , α , β ) = V ( s ; θ , β ) + ( A ( s , a ; θ , α ) − max a ′ ∈ ∣ A ∣ A ( s , a ′ ; θ , α ) ) . \begin{gathered}Q(s,a;\theta,\alpha,\beta)=V(s;\theta,\beta)+\left(A(s,a;\theta,\alpha)-\max_{a'\in|\mathcal{A}|}A(s,a';\theta,\alpha)\right).\end{gathered} Q(s,a;θ,α,β)=V(s;θ,β)+(A(s,a;θ,α)−a′∈∣A∣maxA(s,a′;θ,α)).
注:DuelingNetwork只是改变最优动作价值网络的架构,原本用来训练DQN的策略依然可以使用:
1、优先级经验回放;
2、Double DQN;
3、Multi-step TD;
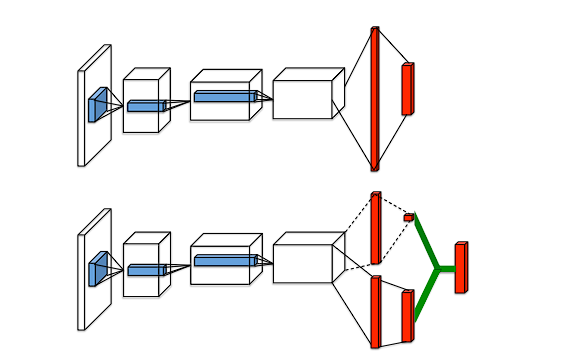
代码实现,只需要将原来的DQN的最优动作价值网络修改成Dueling Network的形式:
class DuelingNetwork(nn.Module):"""QNet.Input: featureOutput: num_act of values"""def __init__(self, dim_state, num_action):super().__init__()# A分支self.a_fc1 = nn.Linear(dim_state, 64)self.a_fc2 = nn.Linear(64, 32)self.a_fc3 = nn.Linear(32, num_action)# V分支self.v_fc1 = nn.Linear(dim_state, 64)self.v_fc2 = nn.Linear(64, 32)self.v_fc3 = nn.Linear(32, 1)def forward(self, state):# 计算Aa_x = F.relu(self.a_fc1(state))a_x = F.relu(self.a_fc2(a_x))a_x = self.a_fc3(a_x)# 计算Vv_x = F.relu(self.v_fc1(state))v_x = F.relu(self.v_fc2(v_x))v_x = self.v_fc3(v_x)# 计算输出x = a_x - v_x - a_x.max()return x