离散化

定义

把无限空间中有限的个体映射到有限的空间中去，以此提高算法的时空效率。通俗的说，离散化是在不改变数据相对大小的条件下，对数据进行相应的缩小。
适用范围：数组中元素值域很大，但个数不是很多。
比如将a[]=[1,3,100,2000,500000]映射到[0,1,2,3,4]这个过程就叫离散化。

两种离散化方式

1.利用sort+unique进行数据离散化（适用于区间查找，及更新）

常与前缀和、树状数组、线段树和动态规范结合考查。

先来看一个金典题目：
题目
假定有一个无限长的数轴，数轴上每个坐标上的数都是 0。
现在，我们首先进行 n次操作，每次操作将某一位置 x 上的数加 c。
接下来，进行 m 次询问，每个询问包含两个整数 l 和 r，你需要求出在区间 [ l , r ] 之间的所有数的和。

输入格式：
第一行包含两个整数 n 和 m。
接下来 n行，每行包含两个整数 x 和 c。
再接下来 m 行，每行包含两个整数 l 和 r。

输出格式：
共 m 行，每行输出一个询问中所求的区间内数字和。

数据范围：
−10⁹ ≤ x ≤ 10⁹

1 ≤ n ≤ 10⁵

1 ≤ m ≤ 10⁵

−10⁹ ≤ l ≤ r ≤ 10⁹

− 10000 ≤ c ≤ 10000
输入样例
3 3
1 2
3 6
7 5
1 3
4 6
7 8
输出样例
8
0
5
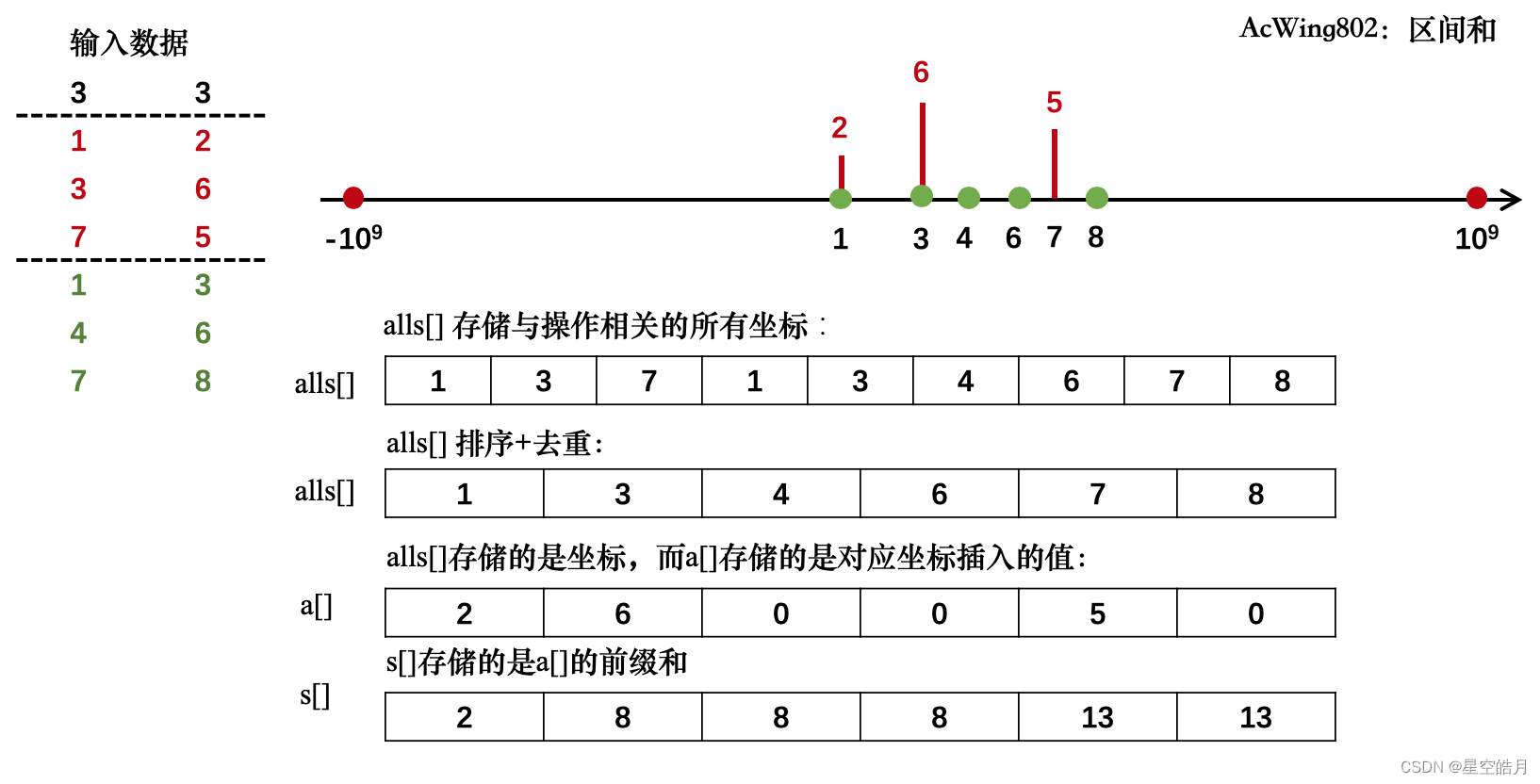
思路：
由于1 ≤ n ≤ 10⁵ 和1 ≤ m ≤ 10⁵ 所调用的数字范围较小，而数轴范围较大，故可以将通过离散化处理，将−10⁹ ≤ x ≤ 10⁹
范围缩为 −10⁵ ≤ x ≤ 10⁵ 左右，大大提高效率。

代码

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
typedef pair<int, int> PII;
const int N = 3 * 1e5 + 10;
int a[N], s[N];
vector<int> alls;
vector<PII> add, query;// 二分查找
int find(int x)
{int l = 0, r = alls.size() - 1;while (l < r){int mid = l + ((r - l) >> 1);if (alls[mid] >= x) r = mid;else l = mid + 1;}return l + 1; // 由于S是从1开始的，所以对应映射位置都往前提一位
}
int main()
{int n, m;cin >> n >> m;for (int i = 0; i < n; ++i){int x, c;cin >> x >> c;add.push_back({x, c});alls.push_back(x);}for (int i = 0; i < m; ++i){int l, r;cin >> l >> r;query.push_back({l, r});alls.push_back(l);alls.push_back(r);}sort(alls.begin(), alls.end());alls.erase(unique(alls.begin(), alls.end()), alls.end());for (auto& item : add){int x = find(item.first);a[x] += item.second;}for (int i = 1; i <= alls.size(); ++i) s[i] = s[i - 1] + a[i];for (auto& item : query){int l = find(item.first), r = find(item.second);cout << s[r] - s[l - 1] << endl;}return 0;
}

当然这里也可以用数组+lower_bound来做，下面会说

1.1 Mayor’s posters POJ - 2528

思路：
可以将问题转化为，求区间的最小值，让每个区间的海报标记为第i个放的，然后用线段树来做。
查询每个海报区间的最小值是否等于i，如果等于i则没有被完全覆盖。本题的数据量太大，区间是[1, 1e7]，
所以要用离散化，存取l和r的相对大小，因为n = 1e4，所以离散过后的区间为[1, 2 * n]。
时间复杂度O(nlogn)

#include<cstdio>
#include<map>
#include<iostream>
#include<algorithm>
#define ls 		rt << 1, l, m
#define rs 		rt << 1 | 1,  m + 1, r
using namespace std;
const int maxn = 2e4 + 5;
int mi[maxn << 2], a[maxn], add[maxn<<2];
struct node{int l, r, pos;
}arr[maxn];
int n;
void pushUp(int rt){mi[rt] = min(mi[rt << 1], mi[rt << 1 | 1]);
}
//下推标记 
void pushDown(int rt){add[rt << 1] = add[rt];add[rt << 1 | 1] = add[rt];mi[rt << 1] = add[rt];mi[rt << 1 | 1] = add[rt];add[rt] = 0;
}
//建树，此过程可用memset代替 
void build(int rt, int l, int r){if (l == r){mi[rt] = 0;return;}int m = (l + r) >> 1;build(ls);build(rs);pushUp(rt);
}
//区间修改 
void update(int rt, int l, int r, int L, int R, int C){if (L <= l && r <= R){mi[rt] = C;add[rt] = C;return;}if(add[rt] != 0)	pushDown(rt);int m = (l + r) >> 1;if (L <= m)		update(ls, L, R, C);if (m < R)		update(rs, L, R, C);pushUp(rt);
}
//查询区间最小值 
int query(int rt, int l, int r, int L, int R){if (L <= l && r <= R){return mi[rt];}if (add[rt] != 0)	pushDown(rt);int m = (l + r) >> 1;int res = maxn;if (L <= m)		res = min(res, query(ls, L, R));if (m < R)		res = min(res, query(rs, L, R));return res;
}
//离散化 
void disc(int cnt){sort(a, a + cnt);int lena = unique(a, a + cnt) - a;for (int i = 0; i < n; ++i){arr[i].l = lower_bound(a, a + lena, arr[i].l) - a + 1;arr[i].r = lower_bound(a, a + lena, arr[i].r) - a + 1;//	printf("l = %d   r = %d\n", arr[i].l, arr[i].r);}
}
void solve(){scanf("%d", &n);build(1, 1, n << 1);int cnt = 0;for (int i = 0; i < n; ++i){scanf("%d%d", &arr[i].l, &arr[i].r);arr[i].pos = i + 1;a[cnt++] = arr[i].l;a[cnt++] = arr[i].r;}disc(cnt);for (int i = 0; i < n; ++i){update(1, 1, n << 1, arr[i].l, arr[i].r, arr[i].pos);} int ans = 0;for (int i = 0; i < n; ++i){int x = query(1, 1, n << 1, arr[i].l, arr[i].r);//printf("x = %d\n", x);if (x == arr[i].pos)	ans++;}printf("%d\n", ans);
}
int main(){int t;scanf("%d", &t);for (int i = 0; i < t; ++i) solve();return 0;
}

1.2 Mayor’s posters POJ - 2528

/*
需要计划你接下来k天的日程。在每一天里.她可以选择学习或者颓废，但是为了劳逸结合，日程表有两类限制:
1、在某个时间段中至少有一天要学习。
2、在某个时间段中至少有一天要颓废。
请问一共有多少种合法的日程表?答案对1000000007取模。
输入格式
第一行三个非负整数k,n,m，分别表示天数，至少有一天学习的时间段个数和至少有一天颓废的时间段个数。
接下来n行，每行两个正整数l,r，表示第l至第r天中至少有一天学习。
接下来m行.每行两个正整数l,r，表示第l至第r天中至少有一天颓废。
输出格式
一行一个整数，表示答案对1000000007取模后的结果。
样例输入 
5 2 2
1 3
3 5
2 2 
4 5
样例输出 
8以下把学习称为填黑，颓废称为填白。先离散化一下，每段有三种情况∶全黑、全白、有黑有白。
最终方案需要满足没有一个连续黑段包含完整的第二类区间,也没有一个连续白段包含完整的第一类区间。
设fi.gi,hi表示从左到右填到第i段，且结尾是黑、白、有黑有白的合法方案数，那么i这个位置往前的最长黑色、白色连续
段长度很容易求出,转移用前缀和优化一下就行了。复杂度瓶颈是离散化。
也有开两个线段树记录最后一个和末尾不同的位置的做法，但是比较难写，常数也较大，可能被卡常。接着，我们使用动态规划来计算填黑和填白的方案数。我们用fs[i]表示以第i个时间段结尾的全填黑的方案数，ft[i]表示以第i个时间段结尾的全填白的方案数，g[i]表示以第i个时间段结尾有黑有白的方案数。对于fs[i]，我们可以根据之前的结果得到，如果第i个时间段全填黑，那么前一个时间段只能全填白或者有黑有白，所以有fs[i] = (sg[i-1] - sg[mt[i]-1] + MOD) % MOD + (st[i-1] - st[mt[i]-1] + MOD) % MOD，其中sg[i]和st[i]分别表示前i个时间段填黑和填白的方案数的前缀和，mt[i]表示以第i个时间段结尾的最短黑色时间段的左端点。对于ft[i]，同理我们有ft[i] = (sg[i-1] - sg[ms[i]-1] + MOD) % MOD + (ss[i-1] - ss[ms[i]-1] + MOD) % MOD，其中sg[i]和ss[i]分别表示前i个时间段填黑和填白的方案数的前缀和，ms[i]表示以第i个时间段结尾的最短白色时间段的左端点。对于g[i]，如果我们在第i个时间段结尾填黑，那么前i-1个时间段可以是全填黑、全填白或者有黑有白，所以有g[i] = ((fs[i-1] + ft[i-1]) % MOD + g[i-1]) * (2^(h[i] - h[i-1]) - 2 + MOD) % MOD，其中2^(h[i] - h[i-1]) - 2表示前i个时间段填黑或填白的所有方案数。
这里2^(h[i] - h[i-1]) - 2表示前i个时间段有黑有白的方案数，一共有h[i]-h[i-1]并且每个时间点可以填黑或填白，所以就是2^(h[i] -h[i-1])。-2是要减去全黑和全白的两种情况。最后答案就是fs[hc] + ft[hc] + g[hc]。*/#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 400005, mod = 1e9 + 7;
/*ls,rs：表示填黑时间段的左端点和右端点lt,rt：表示填白时间段的左端点和右端点hc, h: h表示存填白\黑的时间段左右端点，hc表示一共有多少个时间段 * 2 ，注要多存整个时间段(0, k] fs, ft, g：分别表示全填黑、全填白和有黑有白的方案数。 ss，st，sg：分别是全填黑、全填白和有黑有白的前缀和。ms和mt：ms存的是以R（离散化过后）为右端点的最短黑段的L值，mt同理。
*/
int k, n, m, hc;
int ls[N], rs[N], lt[N], rt[N], h[N], ms[N], mt[N];  
int fs[N], ft[N], g[N], ss[N], st[N], sg[N];
int ksm(int a, int b) { // 快速幂 int x = 1;for (; b > 0; b & 1 ? x = 1ll * x * a % mod : 0, a = 1ll * a * a % mod, b >>= 1);return x;
}
inline int m1(int x) { //求余 return x >= mod ? x - mod : x;
}
inline int input() {int x = 0, F = 1;char c = getchar();while (c > '9' || c < '0') {if (c == '-')F = -1;c = getchar();}while (c <= '9' && c >= '0') {x = x * 10 + c - '0';c = getchar();}return x * F;
}
int main() {k = input();n = input();m = input();for (int i = 1; i <= n; i++)ls[i] = input(), rs[i] = input(), h[++hc] = ls[i] - 1, h[++hc] = rs[i];for (int i = 1; i <= m; i++)lt[i] = input(), rt[i] = input(), h[++hc] = lt[i] - 1, h[++hc] = rt[i];h[++hc] = 0;h[++hc] = k;sort(h + 1, h + hc + 1);hc = unique(h + 1, h + hc + 1) - h - 1; // 排序去重 for (int i = 1; i <= n; i++) { // 填黑 int L = lower_bound(h + 1, h + hc + 1, ls[i] - 1) - h, R = lower_bound(h + 1, h + hc + 1, rs[i]) - h;ms[R] = max(ms[R], L + 1); // L，R是相对大小，以R为右端点，存的是最短的区间}for (int i = 1; i <= m; i++) { // 填白 int L = lower_bound(h + 1, h + hc + 1, lt[i] - 1) - h, R = lower_bound(h + 1, h + hc + 1, rt[i]) - h;mt[R] = max(mt[R], L + 1);}g[1] = sg[1] = 1; // 第一天可填黑可填白ms[1] = mt[1] = 1; // ms和mt保存的是第一个时间段为[1, 1]的值for (int i = 2; i <= hc; i++) {ms[i] = max(ms[i - 1], ms[i]); //黑： 这里找一个以i点为右端点的最大左端点mt[i] = max(mt[i - 1], mt[i]);fs[i] = m1(m1(sg[i - 1] - sg[mt[i] - 1] + mod) + m1(st[i - 1] - st[mt[i] - 1] + mod));// 第i段以i结尾的全填黑 ft[i] = m1(m1(sg[i - 1] - sg[ms[i] - 1] + mod) + m1(ss[i - 1] - ss[ms[i] - 1] + mod));g[i] = 1ll * m1(m1(fs[i - 1] + ft[i - 1]) + g[i - 1]) * (ksm(2, h[i] - h[i - 1]) - 2 + mod) % mod;ss[i] = m1(ss[i - 1] + fs[i]);st[i] = m1(st[i - 1] + ft[i]);sg[i] = m1(sg[i - 1] + g[i]);}printf("%d", m1(m1(fs[hc] + ft[hc]) + g[hc]));return 0;
}

2.利用map或unordered_map进行数据离散化 （使用与非区间操作）

常与差分、并查集、DFS等算法结合考察

2.1 邮票 FZU - 2227【DFS】

题目描述

思路
可以先做映射关系（离散化），然后从最小的数并且这个数出现的次数为1开始dfs，走到哪直接就存到哪。
代码

#include<cstdio>
#include<vector>
#include<map>
#include<cstring>
using namespace std;
const int maxn=1e5+5;
map<int,int>index,data,num;
vector<int>v[maxn];//邻接表，存相对大小的关系 
int cnt,pos;
int dis[maxn];
bool vis[maxn];
void dfs(int x)
{if(cnt==pos)	return;//int len=v[x].size();for(int i=0;i<2;i++) // 题目保证有解，说明一个顶点最多有两个出度{int y=v[x][i];if(!vis[y]){vis[y]=true;dis[pos++]=data[y];dfs(y);}if(cnt==pos)	return;}
}
int main()
{int n;while(scanf("%d",&n)!=EOF){int ui,vi;cnt=0,pos=0;index.clear();data.clear();num.clear();memset(vis,false,sizeof(vis));for(int i=0;i<2*n;i++)	v[i].clear();while(n--){scanf("%d%d",&ui,&vi);if(!num[ui]) {index[ui]=cnt++;data[index[ui]]=ui;//建立映射关系 （1，100） （100，1） }if(!num[vi]){index[vi]=cnt++;data[index[vi]]=vi;}v[index[ui]].push_back(index[vi]);//建立相对大小的对应关系 v[index[vi]].push_back(index[ui]);num[ui]++;num[vi]++;}int st=0;for(map<int,int>::iterator it=num.begin();it!=num.end();it++){if(it->second==1) //判断是否唯一出现，第一个唯一出现的肯定是字典序最小且起始的位置	{st=index[it->first];break;}}vis[st]=true;dis[pos++]=data[st];dfs(st);for(int i=0;i<cnt;i++){printf("%d",dis[i]);if(i<cnt-1)	printf(" ");else	printf("\n");}}
}

2.2 More is better HDU - 1856 【并查集】

题目描述

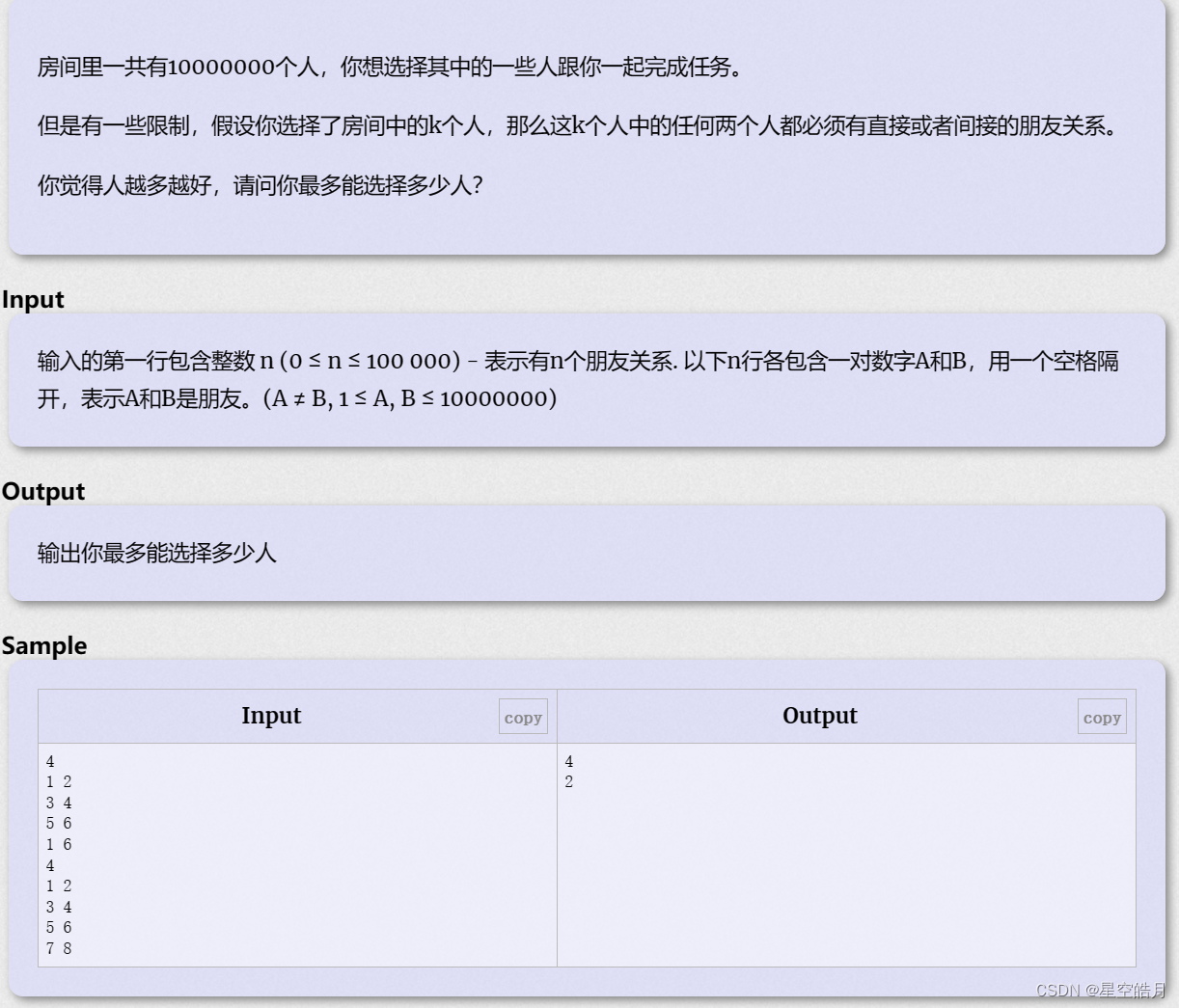
思路：
在集合合并的时，如果两个集合不同，那么在合并成同一个集合的时候，
将被合并的集合里的个数加到这个集合里面，并统计最大值。
坑点：就是当输入n为0时，答案为1，因为当没有朋友对时，各自在自己的房间，所以说答案为1。
代码：

#include<iostream>
#include<cstdio>
#include<map>
#include<utility>
#include<vector>
#include<algorithm>
using namespace std;
const int maxn = 1e5 + 5;
map<int, int> mp;
int fa[maxn], num[maxn], ans = 0;
void init(int n){for (int i = 1; i <= n; ++i){fa[i] = i;num[i] = 1;}
}
int find(int x){return fa[x] == x ? fa[x] : fa[x] = find(fa[x]);
}
void _union(int x, int y){x = find(x);y = find(y);if(x != y){num[y] += num[fa[x]];ans = max(ans, num[y]);fa[x] = y;}
}
void solve(){int n, x, y;while (scanf("%d", &n) != EOF){int cnt = 0;ans = 0;init(maxn); mp.clear();if (n == 0){puts("1");continue;}while (n--){scanf("%d%d", &x, &y);if(!mp[x])	mp[x] = ++cnt;if(!mp[y])	mp[y] = ++cnt;_union(mp[x], mp[y]);}printf("%d\n", ans);}
}
int main(){solve();return 0;
}

2.3 金发姑娘和 N 头牛 - 1952. AcWing题库

题目描述

思路：

代码

#include <iostream>
#include <cstring>
#include <map>
#include <algorithm>using namespace std;const int INF = 2e9;int n, x, y, z;int main()
{map<int, int> b; // 离散化及差分数组cin >> n >> x >> y >> z;for (int i = 0; i < n; i ++ ){//给三个大区间 + cint l, r;cin >> l >> r;//[-INF,r)b[-INF] += x;b[l] -= x;//[l, r]b[l] += y;b[r + 1] -= y;//b(r, INF]b[r + 1] += z;b[INF] -= z;}int res = 0, sum = 0;// 枚举差分数组，求前缀和，更新最大值for(auto item : b){sum += item.second;// 前缀和res = max(res, sum);}cout << res;return 0;
}