题目如岛屿问题解法一文章所介绍，这里不过多赘述，直接讲解第二种解法。

并查集解法

并查集解法的整体思路是，将二维数组中为‘1’的部分提取出来作为样本，再进行判断，如果左上方向有同样为‘1’的，则进行合并，最后看一共有几座岛屿。
不过并查集解法有一个问题，给定的二维数组中是char类型，Java中基本数据都行都会作为值进行传递，那么该怎么分辨二维数组中所有的’1’是不相同的呢？

代码
比较粗糙的做法是用一个类替代这个‘1’，声明一个和参数board等长的Dot类的二维数组，从头至尾遍历一次，将board中为1的位置在Dot数组中对应位置创建Dot对象。
将Dot作为并查集中的样本。利用对象的内存地址不同来区别出不同的1，遍历，进行union后，返回集合个数。
代码主流程中，在进行union时一共进行了三次的遍历。
第一次遍历：只遍历第0列，因为第0列左侧没有值，所以不用考虑左侧。
第二次遍历：只遍历第0行，因为第0行上面没有值，所以不用考虑上面。
第三次遍历：从第1行第1列遍历。只考虑左上方向有没有‘1’，有‘1’则进行合并即可，不用再考虑边界问题。
如果用1个for循环搞定这些，可以。不过常数时间更复杂。每次都要判断边界。

 public static class Node<V> {V val;public Node(V value) {this.val = value;}}public static class Dot {}public static class UnionFind1<V> {HashMap<V, Node<V>> nodes;HashMap<Node<V>, Node<V>> parentMap;HashMap<Node<V>, Integer> sizeMap;public UnionFind1(List<V> lists) {nodes = new HashMap<>();parentMap = new HashMap<>();sizeMap = new HashMap<>();for (V val : lists) {Node node = new Node(val);nodes.put(val, node);parentMap.put(node, node);sizeMap.put(node, 1);}}public Node<V> findParent(Node<V> node) {Stack<Node> stack = new Stack<>();while (node != parentMap.get(node)) {node = parentMap.get(node);stack.push(node);}while (!stack.isEmpty()) {parentMap.put(stack.pop(), node);}return node;}public void union(V a, V b) {Node aNode = findParent(nodes.get(a));Node bNode = findParent(nodes.get(b));if (aNode != bNode) {int aSize = sizeMap.get(aNode);int bSize = sizeMap.get(bNode);Node big = aSize >= bSize ? aNode : bNode;Node small = big == aNode ? bNode : aNode;parentMap.put(small, big);sizeMap.put(big, aSize + bSize);sizeMap.remove(small);}}public int getSize() {return sizeMap.size();}}public static int numIslands2(char[][] board) {int row = board.length;int col = board[0].length;Dot[][] dots = new Dot[row][col];List<Dot> dotList = new ArrayList<>();for (int i = 0; i < row; i++) {for (int j = 0; j < col; j++) {if (board[i][j] == '1') {dots[i][j] = new Dot();dotList.add(dots[i][j]);}}}UnionFind1<Dot> unionFind1 = new UnionFind1<>(dotList);for (int i = 1; i < col; i++) {if (board[0][i - 1] == '1' && board[0][i] == '1') {unionFind1.union(dots[0][i - 1], dots[0][i]);}}for (int i = 1; i < row; i++) {if (board[i - 1][0] == '1' && board[i][0] == '1') {unionFind1.union(dots[i - 1][0], dots[i][0]);}}for (int i = 1; i < row; i++) {for (int j = 1; j < col; j++) {if (board[i][j] == '1') {if (board[i][j - 1] == '1') {unionFind1.union(dots[i][j], dots[i][j - 1]);}if (board[i - 1][j] == '1') {unionFind1.union(dots[i][j], dots[i - 1][j]);}}}}return unionFind1.getSize();}

优化

上面的Dot类很粗糙，为了区别 '1’声明了一个类，很臃肿，所以还可以将上面的方法进行优化。
因为传进来的是一个二维数组，优化的过程是将二维数组拉伸，变成一个一维数组。
根据二维数组的列和行，算出新数组整体的长度，并放到新数组中。
比如说下图：3行4列的数组

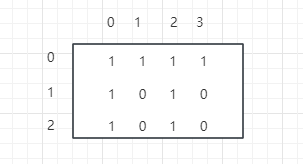
新数组长度 row * col = 12，放入新数组的规则是： 当前行数 * 总列数 + 当前列数，第0行放入新数组中就是数组下标 0 ~ 3，第1行0列的1，放入新数组中就是 1 * 4 + 0 = 4，以此类推。
依然是将二维数组中‘1’部分当做是样本放到并查集中。相同就合并（在新数组中），最后再查看数组中集合个数即可。

代码

 public static int numIslands3(char[][] board) {int row = board.length;int col = board[0].length;UnionFind2 unionFind2 = new UnionFind2(board);for (int i = 1; i < row; i++) {if (board[i - 1][0] == '1' && board[i][0] == '1') {unionFind2.union(i - 1, 0, i, 0);}}for (int j = 1; j < col; j++) {if (board[0][j - 1] == '1' && board[0][j] == '1') {unionFind2.union(0, j - 1, 0, j);}}for (int i = 1; i < row; i++) {for (int j = 1; j < col; j++) {if (board[i][j] == '1') {if (board[i][j - 1] == '1') {unionFind2.union(i, j, i, j - 1);}if (board[i - 1][j] == '1') {unionFind2.union(i, j, i - 1, j);}}}}return unionFind2.getSets();}public static class UnionFind2 {int[] parent;int[] size;int[] help;int col;int sets;public UnionFind2(char[][] board) {int row = board.length;this.col = board[0].length;int len = row * col;parent = new int[len];help = new int[len];size = new int[len];sets = 0;for (int i = 0; i < row; i++) {for (int j = 0; j < col; j++) {if (board[i][j] == '1') {int index = index(i, j);parent[index] = index;size[index] = 1;sets++;}}}}public int index(int row, int currCol) {return row * col + currCol;}// index -> 计算后在parent中的下标;public int findParent(int index) {int num = 0;while (index != parent[index]) {index = parent[index];help[num++] = index;}for (int i = 0; i < num; i++) {parent[help[i]] = index;}return index;}public void union(int r1, int c1, int r2, int c2) {int i1 = index(r1, c1);int i2 = index(r2, c2);int f1 = findParent(i1);int f2 = findParent(i2);if (f1 != f2) {if (size[f1] >= size[f2]) {size[f1] += size[f2];parent[f2] = f1;} else {size[f2] += size[f1];parent[f1] = f2;}sets--;}}public int getSets() {return sets;}}