背景

上午在B站连续刷到两个讲贝叶斯的视频，都讲的极好，而且一个视频是从应用的角度，一个是从原理的角度。我将两个视频反复对照观看发现之前怎么都无感的贝叶斯，这次居然通透了！视频链接我将放到最下方。

正文

第一个看的是从应用的角度去理解贝叶斯，举了一个有趣的例子。
说，妻子回家发现家中出现了一件明显不是自己的女人内衣！于是想知道老公出轨的可能性。而这个例子居然可以套贝叶斯公式。我在此结合两个视频以及自己的理解，来把这个过程说清楚。

条件概率

首先我们需要理解什么是条件概率。
条件概率是指在给定某个事件发生的前提下，另一个事件发生的概率。它表示了一个事件在另一个事件已知发生的条件下的发生概率。

条件概率通常用 P(A|B) 表示，其中 A 和 B 分别代表两个事件。
P(A|B) 表示在事件 B 已经发生的情况下，事件 A 发生的概率。

数学公式为： P(A|B) = P(A∩B) / P(B)

其中，P(A∩B) 表示事件 A 和事件 B 同时发生的概率，P(B) 表示事件 B 发生的概率。

联合概率

上面提到的P(A∩B)就是联合概率，反向推到一下，联合概率就等于：
P(A∩B) = P(A|B) * P(B)
这个公式表示，事件 A 和事件 B 同时发生的概率等于在事件 B 发生的条件下，事件 A 发生的概率与事件 B 发生的概率的乘积。

出轨事件模型带入模型

模型说明

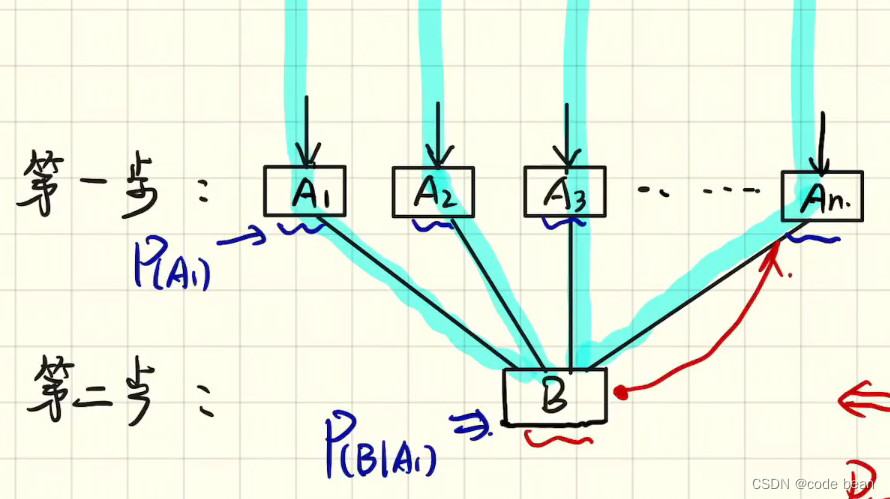
在这里插入图片描述
首先事件B，就是女主在家中发现其它女人的内衣，这个是已经发生的事情了。已经发生的事情还有概率可言吗？

没有啊！所以我们需要的是一个条件概率, P(B|A1) 及A1(出轨事件)发现的情况下家中出现内衣的概率。那么这个条件概率就是 P(B|A1) 。
那已经出轨且家中出现内衣的联合概率就是 P(B|A1) * P(A1)。

那有没有其是其他原因导致家中出现内衣呢？那我们就假设有个一事件A2.
A2事件就是，其实是男主的狐朋狗友把自己女朋友的内衣落在他家了！那于是就有，P(B|A2)
那么男主被坑，且家中出现内衣的联合概率就是 P(B|A2) * P(A2)

当然，还会有其他可能，比如男主其实是买给自己穿的，一个隐藏的女装大佬！概率为 P(B|A3)
那么男主是女装大佬，且家中出现内衣的联合概率就是 P(B|A3) * P(A3)

那么，将这些所有的可能性相加，就得到的是P(B) 的概率，及家中出现内衣的概率。也就是所谓的全概率公式。
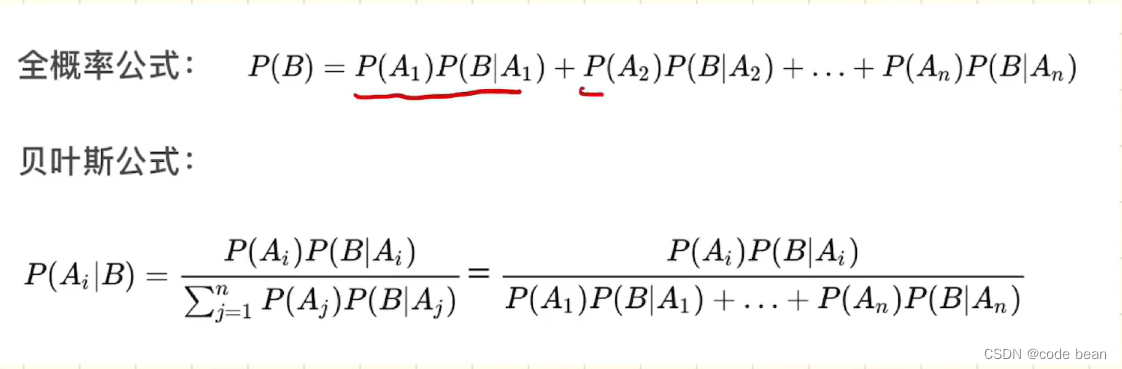
在这里插入图片描述
而全概率其实就是贝叶斯公式的分母。

贝叶斯的目的

那贝叶斯的目的是什么呢？首先我们先了解下，什么叫做先验概率，说人话就是，更具你之前的经验，或者前人的总结和统计来推断的概率。比如硬币的正反根据统计概率就是50% . 再比如，根据男主平时表现，女主推测男主出轨的可能性只有5%。

再次带入模型，之前提到的各种可能事件如果A1出轨事件，其中 P(A1)就是先验概率。 P(B|A1) 就是条件概率。

贝叶斯的目的是，计算出后验概率！

后验概率

后验概率是在考虑了新的证据或数据之后，根据贝叶斯定理计算得出的更新后的事件发生概率。它基于先前的先验概率和新的证据，提供了一个在考虑新信息后的更准确估计。

比如，女主在发现家中出现了其他女人内衣的时候，就需要重新估算男主出轨的概率了。那就需要贝叶斯计算后验概率了。

数学公式为：

P(A|B) = (P(B|A) * P(A)) / P(B)

这里P(B)就是上面提到的，全概率公式：
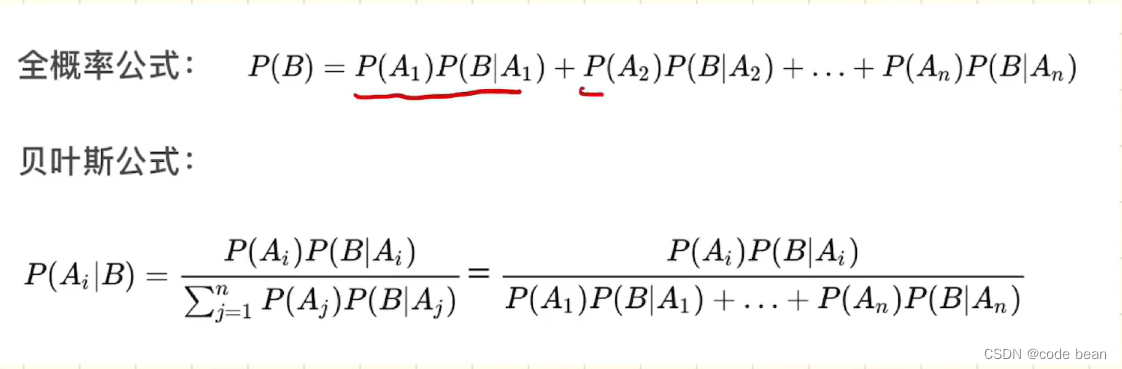
在这里插入图片描述
这里, 我们理解一下，P(A1|B) 和 P(B|A1) 的区别。
A1 表示出轨事件 B 表示出现内衣事件
P(A1|B) 表示的是，在出现内衣的情况下，出轨的可能性，这个是女主一开始的目的，是女主要知道的结果，也就是贝叶斯要计算的的后验概率。

而参数中的P(B|A1) 是表示如果老公出轨了，家中出现女性内衣的可能性！如果老公比较粗心这个可能性就可能是50%，如果是很鸡贼，这个可能就很低。

那么这出轨的概率怎么算？首先我们关注的是出轨的概率，不是被坑以及女装大佬的概率。所以做一个简化。
及先估算出 P(B|A1) 出轨条件下出现内衣的条件概率是51%（男主比较“粗心”），然后其他情况统称A2（被坑+女装大佬），根据条件概率为1的特性，那么P(B|A2)的概率就是49% 而先验概率P(A1) 是根据女主推断是5% P(A2) 其他可能性是 %2 吧。这样就及其了公式左边的所有参数。
这样就可以计算P(A1|B)这个出现内衣后出轨的概率了。

小结

所以，如果男主被证明出轨了，那么女主推断的先验概率P(A1)本来是5%，下次再次发现其他什么新证据时（比如口红）可能P(A1)就会变成80%了。

如果，先验概率时100%呢？那贝叶斯公式就没有意义了，就是说不需要什么新的证据了。也就是不管男主做什么女主都不再信任了。

如果，先验概率为0呢？那后验概率也为0呢？那贝叶斯也没啥意义，后验概率始终为0. 也就是即使男主被女主捉奸在床，女主也不相信男主出轨。

所以，作为人类的我们，不应该该自己的先验概率搞得太高或太低，这样容易极端。

引用

应用视角：https://www.bilibili.com/video/BV1fV411K7ah/?spm_id_from=333.880.my_history.page.click&vd_source=eb730c561c03cdaf7ce5f40354ca252c
理论视角：https://www.bilibili.com/video/BV1a4411B7B4/?spm_id_from=333.880.my_history.page.click

ps 第一个讲应用的视频中公式有个错误，到目前为止该up主，仅仅在评论区说明了问题，后续不知道是否会重新发视频内容，大家看的时候注意一下。