图像的仿射变换涉及到图像的形状位置角度的变化，是深度学习预处理中常用到的功能，仿射变换主要是对图像的缩放，旋转，翻转和平移等操作的组合。

仿射变换：一个任意的仿射变换都能表示为 乘以一个矩阵 (线性变换) 接着再 加上一个向量 (平移).

可以用仿射变换来表示:

• 旋转 (线性变换)
• 平移 (向量加)
• 缩放操作 (线性变换)

图像的仿射变换，如下图所示，图1中的点1, 2 和 3 与图二中三个点一一映射, 仍然形成三角形, 但形状已经大大改变，通过这样两组三点（感兴趣点）求出仿射变换， 接下来我们就能把仿射变换应用到图像中所有的点中，就完成了图像的仿射变换。

一张图好理解；

仿射图像R=变换矩阵M × 原始图像

通常，使用 2x3 大小数组 M 来进行仿射变换。数组由两个矩阵 A、B 组成，其中矩阵 A（大小为2x2）用于矩阵乘法，矩阵 B（大小为2x1）用于向量加法。

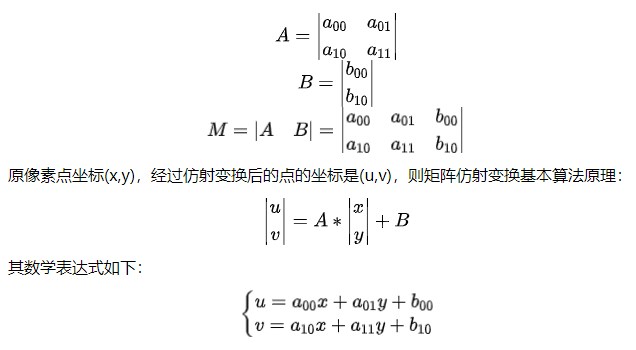
其中：

由于缩放和旋转是通过矩阵乘法来实现，平移是通过矩阵加法来实现的，将这几个操作都用一个矩阵实现所以构造出上面的 2x3 矩阵 M。

仿射变换是从二维坐标到二维坐标之间的线性变换，且为了保持二维图像的“平直性”和“平行性”。我们需要引入齐次坐标的概念，最终得到的齐次坐标矩阵表示形式为：
 

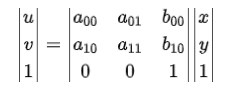
OpenCV学堂 • 来源：Java与Android技术栈 • 2024-03-19 11:11 • 981次阅读

1. 几何变换

图像的几何变换是指将一幅图像中的坐标位置映射到另一幅图像中的新坐标位置，其实质是改变像素的空间位置，估算新空间位置上的像素值。几何变换不改变图像的像素值，只是在图像平面上进行像素的重新安排。

以下是常用的几种几何变换：

旋转：将图像旋转指定角度。

缩放：按缩放因子调整图像大小，使其变大或变小。

平移：将图像从当前位置移动到新位置。

错切：沿特定轴倾斜图像。

仿射变换：一个更广泛的类别，包括单个变换中的缩放、旋转、错切和平移。

透视变换：此变换模拟 3D 空间中的透视效果，允许进行更复杂的操作，例如校正由摄像机角度引起的扭曲。

几何变换通常使用数学函数和变换矩阵来实现。这些矩阵定义了原始图像中的每个像素如何映射到转换图像中的新位置。

2. 仿射变换

2.1 仿射变换

图像处理中的仿射变换是指对图像进行一次线性变换和平移，将其映射到另一个图像空间的过程。仿射变换可以保持图像的“平直性”，即直线经过仿射变换后依然为直线，平行线经过仿射变换后依然为平行线。

通常，使用 2x3 大小数组 M 来进行仿射变换。数组由两个矩阵 A、B 组成，其中矩阵 A（大小为2x2）用于矩阵乘法，矩阵 B（大小为2x1）用于向量加法。

其中：

由于缩放和旋转是通过矩阵乘法来实现，平移是通过矩阵加法来实现的，将这几个操作都用一个矩阵实现所以构造出上面的 2x3 矩阵 M。

仿射变换是从二维坐标到二维坐标之间的线性变换，且为了保持二维图像的“平直性”和“平行性”。我们需要引入齐次坐标的概念，最终得到的齐次坐标矩阵表示形式为：
 

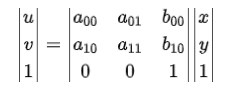
2.2 齐次坐标

在数学里，齐次坐标（homogeneous coordinates），或投影坐标（projective coordinates）是指一个用于投影几何里的坐标系统，如同用于欧氏几何里的笛卡儿坐标一般。齐次坐标可让包括无穷远点的点坐标以有限坐标表示。使用齐次坐标的公式通常会比用笛卡儿坐标表示更为简单，且更为对称。

引入齐次坐标的目的是为了更好的表示无限远（infinity）的坐标的概念，在欧式空间中，无限大或者无限小的坐标的并不存在，不能用数值表示。数学家 August Ferdinand Möbius(1) 提出了齐次坐标系，采用 N+1 个量来表示 N 维坐标。

例如，在二维齐次坐标系中，我们引入一个量 w，将一个二维点 (x,y) 表示为 (X,Y,w) 的形式，其转换关系为
 

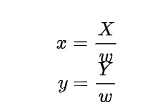
其中，w 可以为任意值。

在笛卡尔坐标系中以(1,2)为例，在齐次坐标系中可以用(1,2,1)表示，也可以用(2,4,2)表示，还可以用 (4,8,4),(8,16,8)...表示，即 (k,2k,k),k∈ R 这些点都映射到欧式空间中的一点，即这些点具有 尺度不变性（Scale Invariant），是“齐性的”(同族的)，所以称之为齐次坐标。

“齐次坐标表示是计算机图形学的重要手段之一，它既能够用来明确区分向量和点，同时也更易用于进行仿射（线性）几何变换。”——出自《计算机图形学(OpenGL版)》的作者 F.S. Hill Jr.

通过齐次坐标还可以证明两条平行线可以相交，非常有意思。

利用仿射函数cv2.warpAffine()可以实现对图像的旋转，其函数的语法格式如下：dst = cv2.warpAffine( src, M, dsize[, flags[, borderMode[, borderValue]]] )

参数解析:
dst ：仿射变换后输出的图像，该图像的类型与原始图像的类型相同，由dsize 决定它的的实际大小。
src ：要进行仿射变换的原始图像。
M ：一个 2×3 的变换矩阵。使用不同的变换矩阵可以实现不同的仿射变换。
dsize：输出图像的尺寸大小。
flags ：插值方法，默认为 INTER_LINEAR。当该值为 WARP_INVERSE_MAP 时，意味着 M 是逆变换类型，实现从目标图像 dst 到原始图像 src 的逆变换。具体可选值可见下表。

程序示例一

利用仿射函数 cv2.warpAffine()实现对图像的平移操作。

import cv2
import numpy as np
lena = cv2.imread("./lena.jpg")  # 读取原图
height, width = lena.shape[:2]  # 获取图像的高度和宽度
x = 120 #向右侧移动 120 个像素
y = 200 #向下方移动 200 个像素
M = np.float32([[1, 0, x], [0, 1, y]])  #转换矩阵M
Panned_lena = cv2.warpAffine(lena, M, (width, height))
cv2.imshow("原始图像", lena)
cv2.imshow("平移图像", Panned_lena)
cv2.waitKey()
cv2.destroyAllWindows()

旋转
  在使用函数 cv2.warpAffine()对图像进行旋转时，可以通过函数 cv2.getRotationMatrix2D()获取转换矩阵。该函数的语法格式为：retval=cv2.getRotationMatrix2D(center, angle, scale)

参数解析：
center ：旋转中心点。
angle ：旋转角度，正数表示逆时针旋转，负数表示顺时针旋转。
scale ：变换尺度（缩放大小）。 利用函cv2.getRotationMatrix2D()可以直接生成要使用的转换矩阵 M。例如，想要以图像中心为圆点，逆时针旋转 60°，并将目标图像缩小为原始图像的 0.7 倍，则在调用函数 cv2.getRotationMatrix2D()生成转换矩阵 M 时所使用的语句为： M=cv2.getRotationMatrix2D((height/2,width/2),60,0.7)

程序示例二
通过函数 cv2.warpAffine()实现图像的旋转。

import cv2
lena = cv2.imread("./lena.jpg")  # 读取原图
height, width = lena.shape[:2]  # 获取图像的高度和宽度
# 以图像中心为圆点，逆时针旋转 60°，并将目标图像缩小为原始图像的 0.7 倍
M = cv2.getRotationMatrix2D((width/2, height/2), 60, 0.7)   #生成转换矩阵M
rotate_lena = cv2.warpAffine(lena, M, (width, height))
cv2.imshow("原始图像", lena)
cv2.imshow("旋转图像", rotate_lena)
cv2.waitKey()
cv2.destroyAllWindows()

更复杂的仿射变换
  对于更复杂仿射变换，OpenCV 提供了函数cv2.getAffineTransform()来生成仿射函数 cv2.warpAffine()所使用的转换矩阵 M。该函数的语法格式为：retval=cv2.getAffineTransform(src, dst)

参数解析：
src：输入图像的三个点坐标。
dst：输出图像的三个点坐标。

  在该函数中，参数 src 和 dst 是包含三个二维数组(x, y)点的数组。上述参数通过函数cv2.getAffineTransform()定义了两个平行四边形。src 和 dst 中的三个点分别对应平行四边形的左上角、右上角、左下角三个点。函数 cv2.warpAffine()以函数cv2.getAffineTransform()获取的转换矩阵 M 为参数，将 src 中的点仿射到 dst 中。函数 cv2.getAffineTransform()对所指定的点完成映射后，将所有其他点的映射关系按照指定点的关系计算确定。

程序示例三
设计程序完成图像仿射变换。

 

透视
  仿射变换可以将矩形映射为任意平行四边形，而透视变换可以将矩形映射为任意四边形。通过函数cv2.warpPerspective()可以实现透视变换，其语法为dst = cv2.warpPerspective( src, M, dsize[, flags[, borderMode[, borderValue]]] )

参数解析：
dst ：透视处理后的输出图像，与原始图像具有相同的类型。dsize 决定输出图像的实际大小。
src：要进行透视变换的图像。
M ：一个 3×3 的变换矩阵。
dsize ：输出图像的尺寸大小。
flags ：插值方法，默认为 INTER_LINEAR。当该值为WARP_INVERSE_MAP 时，意味着 M 是逆变换类型，能实现从目标图像 dst 到原始图像 src 的逆变换，具体可选值参见下表。

borderMode ：边类型， 默认为 BORDER_CONSTANT 。 当 该值为 BORDER_TRANSPARENT 时，意味着目标图像内的值不做改变，这些值对应原始图像内的异常值。
borderValue ：边界值，默认为 0。

  与仿射变换函数一样，同样可以使用一个函数来生成函数 cv2.warpPerspective()所使用的转换矩
阵。该函数是 cv2.getPerspectiveTransform()，其语法格式为：retval = cv2.getPerspectiveTransform( src, dst )

参数解析：
src ：输入图像的四个顶点的坐标。
dst ：输出图像的四个顶点的坐标。

  与仿射变换函数cv2.getAffineTransform()不同的。需要注意的是， src 参数和 dst 参数是包含四个点的数组，实际使用中，可以根据需要控制 src 中的四个点映射到 dst 中的四个点。

程序示例四
设计程序，完成图像透视。

import cv2
import numpy as np
lena=cv2.imread('./lena.jpg')    #导入原图
rows,cols=lena.shape[:2] #获取图像的行数和列数
pts1 = np.float32([[150,50],[400,50],[60,450],[310,450]])
pts2 = np.float32([[50,50],[rows-50,50],[50,cols-50],[rows-50,cols-50]])
M=cv2.getPerspectiveTransform(pts1,pts2)    #转换矩阵M
dst=cv2.warpPerspective(lena,M,(cols,rows))
cv2.imshow("lena",lena)
cv2.imshow("dst",dst)
cv2.waitKey()
cv2.destroyAllWindows()

在指定原始图像中的平行四边形顶点pts1,指定目标图像中矩形的四个顶点pts2，使用M=cv2.getPerspectiveTransform(pts1,pts2)生成转换矩阵 M。接下来，使用语句dst=cv2.warpPerspective(img,M,(cols,rows))完成从平行四边形到矩形的转换。程序运行结果如下：

重映射
  把一幅图像中的某个位置的像素点放置到另一幅图像内的指定位置的过程为图像的重映射。OpenCV提供的重映射函数 cv2.remap()可以实现自定义的方式的重映射。其语法格式为dst = cv2.remap( src, map1, map2, interpolation[, borderMode[, borderValue]] )

参数解析：
dst ：目标图像，与src 有相同的大小和类型。
src ：原始图像。
map1 ：该参数有两种可能的值：①表示(x,y)点的一个映射；②表示 CV_16SC2 , CV_32FC1, CV_32FC2 类型(x,y)点的 x 值。
map2 ：该参数有两种可能的值：①当 map1 表示(x,y)时，该值为空。②当 map1 表示(x,y)点的 x 值时，该值是 CV_16UC1, CV_32FC1 类型(x,y)点的 y 值。
Interpolation ：插值方式，这里不支持 INTER_AREA 方法，具体值参见下表。

borderMode ：边界模式。当该值为 BORDER_TRANSPARENT 时，表示目标图像内的对应源图像内奇异点的像素不会被修改。
borderValue：边界值，默认为 0。

  重映射是通过修改像素点的位置得到一幅新图像。在构建新图像时，需要确定新图像中每个像素点在原始图像中的位置。因此，映射函数的作用是查找新图像像素在原始图像内的位置。

  重映射是将新图像像素映射到原始图像的过程，因此被称为反向映射。在函数 cv2.remap()中，参数 map1 和参数 map2 用来说明反向映射，map1 针对的是坐标 x，map2 针对的是坐标 y。

  因为参数 map1 和参数 map2 的值是浮点数，所以目标图像可以映射回一个非整数的值，这意味着目标图像可以“反向映射”到原始图像中两个像素点之间的位置（当然，该位置是不存在像素值的）。而且由于参数 map1 和参数 map2 的值是浮点数，所以通过函数 cv2.remamp()实现的映射关系变得更加随意，可以通过自定义映射参数实现不同形式的映射。

5.1 复制
  在映射时，通过将 map1 和map2的值分别设定为对应位置上的 x 轴坐标和 y 轴坐标值，可以让函数 cv2.remap()实现图像复制。

程序示例五
使用函数 cv2.remap()完成对图像的复制。

绕x轴旋转
  如果想要图像绕x轴翻转，则在映射过程中需要满足：①x坐标轴的值保持不变；②y坐标轴的值以x轴为对称轴进行交换。

  反映在 map1 和 map2 上就是map1 的值保持不变，map2 的值调整为“总行数-1-当前行号”。

  需要注意，OpenCV 中行号的下标是从 0 开始的，所以在对称关系中存在“当前行号+对称行号=总行数-1”的关系。因此在绕着 x 轴翻转时，map2 中当前行的行号调整为“总行数-1-当前行号”。

程序示例六
使用函数 cv2.remap()实现对图像绕 x 轴翻转。

import cv2
import numpy as np
lena=cv2.imread("./lena.jpg")
rows,cols=lena.shape[:2]
map1 = np.zeros(lena.shape[:2],np.float32)
map2 = np.zeros(lena.shape[:2],np.float32)for i in range(rows):for j in range(cols):map1.itemset((i,j),j)map2.itemset((i,j),rows-1-i)
rst=cv2.remap(lena,map1,map2,cv2.INTER_LINEAR)cv2.imshow("原始图像",lena)
cv2.imshow("绕x轴旋转图像",rst)
cv2.waitKey()
cv2.destroyAllWindows()

 

绕y轴旋转
  如果想要图像绕y轴翻转，则在映射过程中需要满足：①y坐标轴的值保持不变；②x坐标轴的值以y轴为对称轴进行交换。

  反映在 map1 和 map2 上就是map2 的值保持不变，map1 的值调整为“总行数-1-当前列号”。

  需要注意，OpenCV 中列号的下标是从 0 开始的，所以在对称关系中存在“当前列号+对称列号=总列数-1”的关系。因此在绕着 y 轴翻转时，map2 中当前行的行号调整为“总列数-1-当前列号”。

程序示例七
使用函数 cv2.remap()实现对图像绕 y 轴翻转。

import cv2
import numpy as np
lena=cv2.imread("./lena.jpg")
rows,cols=lena.shape[:2]
map1 = np.zeros(lena.shape[:2],np.float32)
map2 = np.zeros(lena.shape[:2],np.float32)for i in range(rows):for j in range(cols):map1.itemset((i,j),cols-1-j)map2.itemset((i,j),i)
rst=cv2.remap(lena,map1,map2,cv2.INTER_LINEAR)cv2.imshow("原始图像",lena)
cv2.imshow("绕y轴旋转图像",rst)
cv2.waitKey()
cv2.destroyAllWindows()

绕x轴、y轴翻转
  如果想让图像绕着 x 轴、y 轴翻转，意味着在映射过程中：①x 坐标轴的值以 y 轴为对称轴进行交换；②y 坐标轴的值以 x 轴为对称轴进行交换。

  反映在 map1 和 map2 上： map1 的值调整为“总列数-1-当前列号”； map2 的值调整为“总行数-1-当前行号”。

程序示例八
使用函数 cv2.remap()实现图像绕 x 轴、y 轴翻转。

import cv2
import numpy as np
lena=cv2.imread("./lena.jpg")
rows,cols=lena.shape[:2]
map1 = np.zeros(lena.shape[:2],np.float32)
map2 = np.zeros(lena.shape[:2],np.float32)for i in range(rows):for j in range(cols):map1.itemset((i,j),cols-j-1)map2.itemset((i,j),rows-1-i)
rst=cv2.remap(lena,map1,map2,cv2.INTER_LINEAR)cv2.imshow("原始图像",lena)
cv2.imshow("绕x轴、y轴旋转图像",rst)
cv2.waitKey()
cv2.destroyAllWindows()

x轴、y轴互换
  如果想让图像的 x 轴、y 轴互换，意味着在映射过程中，对于任意一点，都需要将其 x 轴、y 轴坐标互换。反映在 map1 和 map2 上就是：①map1 的值调整为所在行的行号；②map2 的值调整为所在列的列号。

  需要注意的是，如果行数和列数不一致，上述运算可能存在值无法映射的情况。默认情况下，无法完成映射的值会被处理为 0。

程序示例九
使用函数 cv2.remap()实现图像绕 x 轴、y 轴互换。

import cv2
import numpy as np
lena=cv2.imread("./lena.jpg")
rows,cols=lena.shape[:2]
map1 = np.zeros(lena.shape[:2],np.float32)
map2 = np.zeros(lena.shape[:2],np.float32)for i in range(rows):for j in range(cols):map1.itemset((i,j),i)map2.itemset((i,j),j)
rst=cv2.remap(lena,map1,map2,cv2.INTER_LINEAR)cv2.imshow("原始图像",lena)
cv2.imshow("x轴、y轴互换图像",rst)
cv2.waitKey()
cv2.destroyAllWindows()